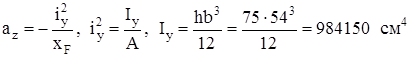ТЕМА 6. Внецентренное сжатие прямого бруса

Внецентренное сжатие является частным случаем сложного сопротивления при котором брус (колонна) сжимается силами, параллельными оси бруса (рис. 6.1).

 

Поперечное сечение

 

Рисунок 6.1

e_z и e_у – эксцентриситеты приложения силы F.

В произвольном поперечном сечении при данной нагрузке действуют такие внутренние силовые факторы: N_x, M_y, M_z.

N_x = - F, M_y = ± F · eу, M_z = ± F · ez

Следовательно нормальное напряжение в произвольной точке сечения будет состоять из напряжений осевого сжатия силой N_х, и напряжений от чистого изгиба моментами М_у и M_z в обеих главных плоскостях.

Нормальные напряжения в любой точке поперечного сечения можно определить ,

А – площадь поперечного сечения;

M_z и M_y – изгибающие моменты относительно осей Оz и Оу;

I_z и I_у – осевые моменты инерции для прямоугольного сечения

 

где у_А и z_А – координаты точки, в которой определяется напряжение.

В контурных точках прямоугольного сечения нормальное напряжение можно определить по формуле:

,

где W_z и W_у – моменты сопротивления для прямоугольного сечения

Нейтральная линия сечения (линия нулевых напряжений), пересекает координатные оси в точках, которые принадлежат квадранту, противоположному тому, в котором лежит сила F.

Нулевую линию можно построить графически, соединяя точки нулевых значений напряжения на построенных по граням сечения эпюр σ или определить отрезки а_z и а_у, которые отсекаются нейтральной линией на осях у и z.

і_у и і_z – радиусы инерции.

 

КОНТРОЛЬНОЕ ЗАДАНИЕ № 10

Внецентренное сжатие

Для колонны с прямоугольным поперечным сечением (рис. 6.2) с размерами и нагрузкой которые следует взять в соответствии собственному шифру из таблицы 10 необходимо:

Рисунок 6.2

Вычислить нормальные напряжения в угловых точках контура поперечного сечения.

Построить эпюры нормальных напряжений на гранях сечения.

Определить положение нейтральной оси графически и аналитически (то есть определить отрезки, которые нулевая линия отсекает на координатных осях).

Расчет выполнить без учета собственного веса колонны.

 

Таблица 10

Номер строки	F (кн.)	а (см)	Координаты точки приложения силы
YF (см)	ZF (см)
			-8
			-12
			-6	-6
				-8
			-10	-10
				-12
			-14	-14

 

 

Пример. Дляколонны с прямоугольным поперечным сечением (рис 6.2) вычислить нормальные напряжения в угловых точках (1,2,3,4) контура поперечного сечения; построить эпюры нормальных напряжений на гранях сечения, а также определить положение нейтральной оси графически и аналитически и сравнить результаты обоих вариантов.

 

Исходные данные:

F = 150 кН, y_F = +12см, z_F = -12 см, а = 54 см (рис. 6.3)

Определяем нормальные напряжения в контурных точках сечения σ₁, σ₂, σ₃, σ₄.

 

N = F = 150кН, А = 54·75 = 4050см2

M_х = M_y = 150·12 = 1800 кН·см

 

Рисунок 6.3

 

Для определения знаков слагаемых M_z и M_y воспользуемся рис. 6.4.

Рисунок 6.4

 

σ₁= -0,037-0,035-0,049 = -0,121 (кН/см2)

σ₂= -0,037-0,035+0,049 = -0,023 (кН/см2)

σ₃= -0,037+0,035+0,049 = +0,047 (кН/см2)

σ₄ = -0,037+0,035-0,049 = -0,051 (кН/см2)

2 Строим эпюры нормальных напряжений по граням сечения по полученным значениям (рис. 6.5).

 

Рисунок 6.5

3 Определения положения нейтральной оси:

а) для графического построения нейтральной оси (н. оси) проектируем точки нулевых напряжений построенных эпюр σ (рис. 6.5) на контур сечения и соединив их прямой линией получаем графическое положение н. оси. Для точного определения положения н. оси сечение должно быть построено в масштабе;

б) аналитическое определение отрезков а_z и а_у, которые н. ось отсекает от координатных осей ОZ и ОУ.

Откладываем полученные отрезки на осях координат, соединяем полученные точки прямой, получаем нейтральную ось.