Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1 Построение эпюр внутренних усилийСтр 1 из 8Следующая ⇒
Методические указания для самостоятельного выполнения контрольных заданий при изучении курса “Сопротивление материалов”
Харьков 2014
Министерство образования и науки Украины Харьковский НАЦИОНАЛЬНЫЙ университет Строительства и архитектуры
Методические указания для самостоятельного выполнения контрольных заданий при изучении курса “Сопротивление материалов” для студентов всех специальностей
Утверждено на заседании кафедры строительной механики. Протокол № 10 от 15.06.14.
Харьков 2014 Методические указания для самостоятельного выполнения контрольных заданий при изучении курса “Сопротивление материалов” для студентов всех специальностей / Составители: С.А. Ворончихина, А.В. Медведева, В.Ю. Мирошников, С.В. Олешкевич. – Харьков: ХНУСА, 2014. – 71 с.
Рецензент В.А. Воблих
Кафедра строительной механики
Введение
Основная цель изучения курса заключается в предоставлении дополнительной широты инженерных знаний, связанных с дисциплиной «Сопротивление материалов», умение правильно выбирать материалы и конструктивные формы, которые будут обеспечивать надежность и долговечность конструкций при соблюдении определенного уровня экономичности, правильно выбирать расчетные схемы, при выполнении расчетов типичных элементов конструкций, сравнении вариантов, нахождении оптимальных решений инженерных задач. Методические указания и задания разработаны в соответствии с рабочей программой дисциплины «Сопротивление материалов» для самостоятельного выполнения контрольных заданий при изучении курса. Рабочая программа разработана на основе образовательно-профессиональной программы высшего образования Министерства образования и науки Украины за направлением «Промышленное и гражданское строительство». В результате изучения дисциплины студент должен знать вид и характер нагрузок, характер поведения разных видов материалов и их механические характеристики, переход от реальной конструкции к ее расчетной схеме, виды деформаций упругих систем. Студент должен уметь выполнять расчет на прочность и жесткость для отдельных видов деформации и подбирать необходимые размеры сечений, для сжатого стержня выполнять расчет на устойчивость, четко представлять функциональную связь между внешними силами и законами распределения внутренних сил в элементах конструкции, анализировать причины появления и развития возможных повреждений и определять факторы разрушения материалов. Студенту необходимо ознакомиться с экспериментальными методами работы разных материалов конструкций под действием внешней нагрузки, определением физических характеристик материалов. Знание этих методов дает представление о работе отдельных конструкций в здании, что позволяет с более профессиональным подходом проектировать сложные архитектурные элементы.
Основными видами изучения дисциплины «Сопротивление материалов» есть лекции, лабораторные и практические занятия, а также самостоятельная работа студента. Дисциплина предусматривает изучение методов расчета на прочность, жесткость и устойчивость упругих тел при действии внешних сил, обеспечивает соответствующий уровень подготовки специалиста в общих инженерных науках. Для усвоения дисциплины необходимо знание курсов таких дисциплин, как высшая математика, физика, теоретическая механика, строительные материалы. Знания и практические навыки, приобретенные при изучении дисциплины, применяются в курсах строительной механики, металлических, деревянных и железобетонных конструкций. В методических указаниях приведены контрольные задания для самостоятельного изучения курса с примерами и указаниями к их выполнению. Каждое контрольное задание должно содержать графическую часть, выполненную на стандартном листе бумаги, и пояснительную записку, в которой приведены все вычисления с необходимыми пояснениями в сокращенной форме.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 1 Таблица 1
КОНТРОЛЬНОЕ ЗАДАНИЕ №2 Таблица 2
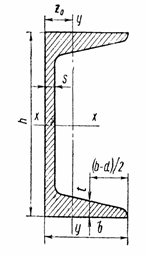
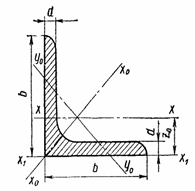
Рисунок 2.2 Пример: Определить геометрические характеристики плоского сечения (рис.2.3) и положение главных осей инерции: zгл, угл.
1 Выбираем произвольные оси Z, Y. 2 Определяем координаты центра тяжести сечения: Уц.т. = 7.4 см. Zц.т. = 2.4 см. 3 Вычисляем моменты инерции относительно осей центра тяжести сечения:
а) осевые Iz = Iy = б) центробежный Izy = 4 Определяем положение главных осей инерции: zгл, угл. tq2a0== 2a0 = + 280 41¢ a0 = + 14020¢
Знак плюс означает, что угол a0 нужно отложить против часовой стрелки.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 3 КОНТРОЛЬНОЕ ЗАДАНИЕ № 4 Таблица 4
Рисунок 3.3
КОНТРОЛЬНОЕ ЗАДАНИЕ № 5 Изгиб консольной балки
Для заданных схем балок (рис. 3.4) с размерами и нагрузками, которые следует взять соответственно собственному шифру из таблицы 5, необходимо: 1 Построить эпюры изгибающих моментов – Мz и поперечных сил – Qy. 2 Подобрать прямоугольное поперечное сечение, соотношение сторон которого известно, а расчетное сопротивление на изгиб равняется: R = 14 МПа = 1,4 кН/см2 3 Определить наибольшее касательное напряжение τmax.
Таблица 5
Рисунок 3.4
Пример. Для заданной балки (рис 3.5) построить эпюры Мz и Qy; подобрать прямоугольное поперечное сечение, соотношение сторон h/b = 1,4; расчетное сопротивление на изгиб R = 14 МПа = 1,4 кН/см2; определить наибольшее касательное напряжение τmax.
0 ≤х1≤ 1,2м
Qy= +8·х1 х1 = 0 Qy = 0 х1 =1,2м Qy =+9,6кН
Qy = 8·1,2 – 60 = - 50,4 кН
Рисунок 3.5
2 Подбираем прямоугольное поперечное сечение при h/b = 1,4 Rизг = 1,4 кН/см2
3 Определяем наибольшее касательное напряжение τ max (рис. 3.6).
Qymax = 50,4кН b = 26,6см
Рисунок 3.6
Szполусечение = 26,6·18,6·9,3 = 4601,3 см3
τmax = 0,08 кН/см2
КОНТРОЛЬНОЕ ЗАДАНИЕ №6 Изгиб однопролетной балки
Для заданных схем балок (рис. 3.7) с размерами и нагрузкой, которые следует взять соответственно собственному шифру из таблицы 6 необходимо:
1 Построить эпюры изгибающих моментов Mz и поперечных сил Qy. 2 Подобрать двутавровое поперечное сечение при расчетном сопротивлении R = 220 МПа = 22кН/см2 3 Проверить прочность балки на срез при Rсрез. = 130 МПа = 13кН/см2
Рисунок 3.7
Таблица 6
Пример. Для заданной балки (рис 3.8) построить эпюры Mz и Qy; подобрать двутавровое поперечное сечение при расчетном сопротивлении R = 22кН/см2; проверить прочность балки на срез Rсрез = 13кН/см2
1 Строим эпюры Qy и Mz. Определяем опорные реакции
∑Мв = 0 - Rа ·5,1+16·2,5·3,85+20·7,9=0 Rа = +61,2кН ∑Ма = 0 + Rв ·5,1-16·2,5·1,25+20·2,8=0 Rв = -1,2кН ∑Fу = 0 -20+61,2-16·2,5-1,2=0 0 ≤ x1 ≤ 2,6м
Mz = -1,2·х1 Qy= +1,2кН 0 ≤ x2 ≤ 2,8м
Mz = -20·х2 0 ≤ x3 ≤ 2,5м
2 Подбираем сечение двутаврового профиля при R = 22кН/см2
По сортаменту (приложение А) принимаем двутавр
3 Проверяем прочность на срез Rсрез = 13кН/см2
Условие прочности по касательным напряжениям выполняется. КОНТРОЛЬНОЕ ЗАДАНИЕ № 7 КОНТРОЛЬНОЕ ЗАДАНИЕ № 8 КОНТРОЛЬНОЕ ЗАДАНИЕ № 9 Определение перемещений Для заданной схемы рамы (рис. 5.8) найти вертикальное перемещение сечения А - Vа и угол поворота сечения В - Өв от действия равномерно распределенной нагрузки с интенсивностью - g и сосредоточенной силой F = Данные берем из таблицы 9. Таблица 9
Рисунок 5.8
1. Строим эпюру от внешней нагрузки М F (рис 5.10) 0 ≤ x1 ≤ 2,9м
0 ≤ y1 ≤ 2,9м
Рисунок 5.9
0 ≤ x2 ≤ 2,4м МF =62·2,9- x2 = 0 М F = -38,8 кН·м x2 = 2,4м М F = -550,5 кН·м 2. Вычисляем вертикальное пере-мещение в точке А-Vа. Для этого в точке А прикладываем вертикально силу F = 1 и от ее действия строим эпюру
умножаем на эпюру МF на Рисунок 5.10 одноименных элементах.
Рисунок 5.11 0 ≤ Х1 ≤ 2,4м
При перемножении эпюр используем правило Верещагина.
Знак „минус” указывает на то, что перемещение сечения в точке А происходит в направлении противоположном единичной силе. 3 Определяем угол поворота поперечного сечения в точке В. Для этого в точке В прикладываем момент М = 1 и строим эпюру Для определения угла поворота сечения - Өв, перемножаем эпюры М F (рис. 5.10) и
Рисунок 5.12 0 ≤ Х2 ≤ 5,3м __ МВ = +1
То есть поворот сечения в точке В происходит по часовой стрелке.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 10 Внецентренное сжатие Для колонны с прямоугольным поперечным сечением (рис. 6.2) с размерами и нагрузкой которые следует взять в соответствии собственному шифру из таблицы 10 необходимо:
Рисунок 6.2 Вычислить нормальные напряжения в угловых точках контура поперечного сечения. Построить эпюры нормальных напряжений на гранях сечения. Определить положение нейтральной оси графически и аналитически (то есть определить отрезки, которые нулевая линия отсекает на координатных осях). Расчет выполнить без учета собственного веса колонны.
Таблица 10
Пример. Дляколонны с прямоугольным поперечным сечением (рис 6.2) вычислить нормальные напряжения в угловых точках (1,2,3,4) контура поперечного сечения; построить эпюры нормальных напряжений на гранях сечения, а также определить положение нейтральной оси графически и аналитически и сравнить результаты обоих вариантов.
Исходные данные: F = 150 кН, yF = +12см, zF = -12 см, а = 54 см (рис. 6.3) Определяем нормальные напряжения в контурных точках сечения σ1, σ2, σ3, σ4.
N = F = 150кН, А = 54·75 = 4050см2
Mх = My = 150·12 = 1800 кН·см

Для определения знаков слагаемых Mz и My воспользуемся рис. 6.4.
Рисунок 6.4
σ1= -0,037-0,035-0,049 = -0,121 (кН/см2) σ2= -0,037-0,035+0,049 = -0,023 (кН/см2) σ3= -0,037+0,035+0,049 = +0,047 (кН/см2) σ4 = -0,037+0,035-0,049 = -0,051 (кН/см2) 2 Строим эпюры нормальных напряжений по граням сечения по полученным значениям (рис. 6.5).
Рисунок 6.5 3 Определения положения нейтральной оси: а) для графического построения нейтральной оси (н. оси) проектируем точки нулевых напряжений построенных эпюр σ (рис. 6.5) на контур сечения и соединив их прямой линией получаем графическое положение н. оси. Для точного определения положения н. оси сечение должно быть построено в масштабе; б) аналитическое определение отрезков аz и ау, которые н. ось отсекает от координатных осей ОZ и ОУ.
Откладываем полученные отрезки на осях координат, соединяем полученные точки прямой, получаем нейтральную ось. КОНТРОЛЬНОЕ ЗАДАНИЕ № 11 Пример Для заданного стального стержня двутаврового поперечного сечения центрально сжатого силой F (рис. 7.4) необходимо: 1 Подобрать поперечное сечение стержня (определить номер двутавра). 2 Определить критическую силу Fкр. 3 Вычислить коэффициент запаса на устойчивость – n. Исходные данные: F = 410 кН, Для правильного выполнения расчетов необходимо ознакомиться с разделом сопротивления материалов „Устойчивость сжатого стержня”, в частности той частью, которая относится к практическим расчетам на устойчивость. Подбор сечения сжатого стержня выполняют по условию устойчивости:
где N – продольная сила, что равняется силе F, прилагаемой к стержню; А – площадь поперечного сечения сжатого стержня; R = [σ] – допустимое нормальное напряжение на сжатие (расчетное сопротивление); φ – коэффициент снижения расчетного сопротивления, безразмерная величина, которая зависит от гибкости стержня (λ).
где λ – гибкость стержня;
іmin – минимальный радиус инерции поперечного сечения сжатого стержня; μ – коэффициент приведенной длины, зависит от условий закрепления стержня (рис. 7.2). 1 Сечение подбираем из условия устойчивости Формула содержит две неизвестные величины: А и φ, поэтому расчет выполняем методом последовательных приближений, задавая φ произвольно (табл. 11).
φ1 = 0,5; Обращаемся к таблице сортамента ГОСТ 8239-89 – двутавры (приложение А). Ближайшее значение площади сечения к А1 = 53,8 см2, что отвечает двутавру № 33 минимальный радиус инерции которого іу = 2,79 см. Тогда гибкость стержня двутавра № 33 равна, учитывая, что μ=0,7, а длина ℓ = 290 см
Определяем коэффициент φ1', что отвечает гибкости λ1 = 72,76 единиц:
б) второе приближение расчета:
За таблицей сортамента ближайшее значение площади А2 = 40,2 см2 І№27, іmin = 2,54см. Соответственно, гибкость стержня с поперечным сечением І№27 равняется:
в) третье приближение расчета:
За таблицей сортамента ближайшее значение площади отвечает двутавру І № 24а; А3 = 37,5 см2; іmin = іу = 2,63
г) четвертое приближение:
За таблицей сортамента (приложение А) отвечает двутавру І№24 А=34,8см2. Признаком завершения процесса подбора сечения является получение двух близких значений коэффициента φ (погрешность до 2%) и выполнения условия прочности. Проверим выполнение условия прочности:
11,78 ≤ 11,776 Окончательно подбираем сечение сжатого стержня І № 24 (рис 7.5).
Iz = 3460 см4; іz = 9,97см Iy = 198 см4; іy = 2,37 см
2 Определяем критическую силу для заданного стержня. Формула для определения Fкр, зависит от величины гибкости, что подтверждается известным графиком зависимости σ и λ (рис.7.1). Гибкость менее ста единиц. Тогда критическое напряжение равняется: Рисунок 7.5 σкр = а - b λ = 31-0,114·85,65 = 21,24 кН/ см2 Fкр = σкр · АІ = 21,24 3 Коэффициент запаса на устойчивость равняется:
Из теоретических исследований известно, что для стальных длинных сжатых стержней значение коэффициента запаса на устойчивость лежит в границах: n = 1,5 ÷ 3. Полученный ответ находится в необходимых границах.
ПРИЛОЖЕНИЕ А Сортамент прокатной стали в соответствии с ГОСТ 8239-72*, 8240-72*, 8510-72 Двутавры
Таблица А.1 - Сортамент прокатной стали - двутавры
ПРИЛОЖЕНИЕ Б Швеллеры
Таблица Б.1 - Сортамент прокатной стали – швеллеры
ПРИЛОЖЕНИЕ В Уголки равнобокие
Таблица В.1 - Сортамент прокатной стали -уголки равнобокие
Продолжение таблицы В.1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.94.152 (0.229 с.) |
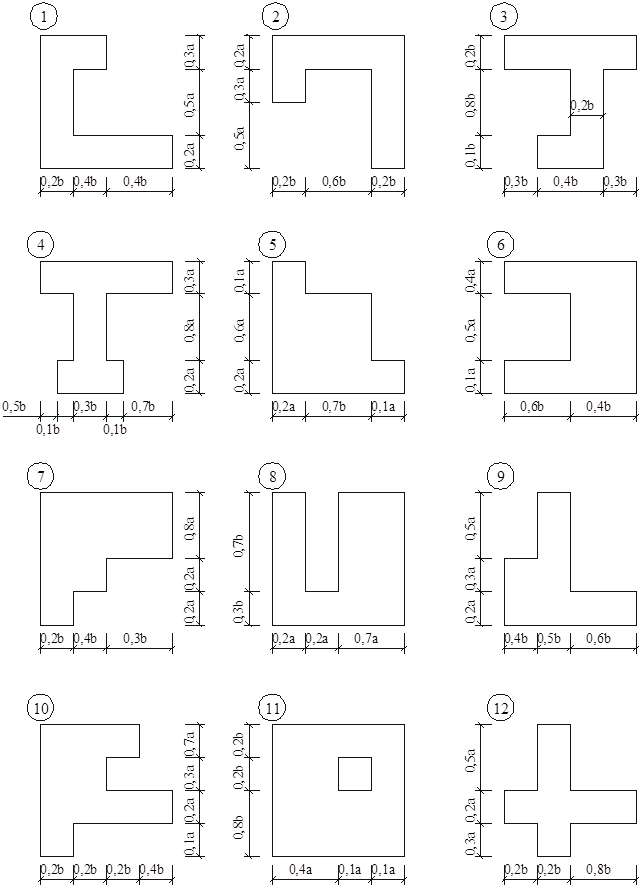
 Разбиваем данную фигуру на простые.
Разбиваем данную фигуру на простые.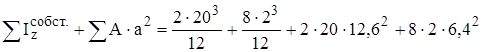 = 2264.42 см4.
= 2264.42 см4. = 384.42 см4.
= 384.42 см4.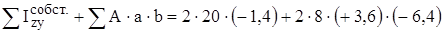 = - 514.24 см4.
= - 514.24 см4.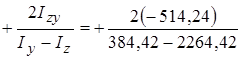 = +0,5471
= +0,5471

 1 Строим эпюры Qy и Мz с использованием правила знаков приведенного на рис. 1.8
1 Строим эпюры Qy и Мz с использованием правила знаков приведенного на рис. 1.8

 0 ≤ x2 ≤ 0,8м
0 ≤ x2 ≤ 0,8м Мz = - 8 · 1,2 (х2 + 0,6) + 60 х2 + 45
Мz = - 8 · 1,2 (х2 + 0,6) + 60 х2 + 45 см3
см3 ;
; 
 ; 0,3 b3 = 5682 см2
; 0,3 b3 = 5682 см2 см, b = 26,6см, h = 37,2см.
см, b = 26,6см, h = 37,2см.






 Qy= -20кН
Qy= -20кН Qy= -20+61,2-16· х3
Qy= -20+61,2-16· х3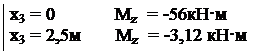 Mz = -20·(х3 +2,8)+61,2·х3 -
Mz = -20·(х3 +2,8)+61,2·х3 - 

 №22, у которого Iz = 2790см4, Szполусечение = 143 см3, d = 0,54 см.
№22, у которого Iz = 2790см4, Szполусечение = 143 см3, d = 0,54 см.

 .
.
 Пример. Для заданной рамы (рис. 5.9) вычислить вертикальное перемещение сечения А-Vа и угол поворота сечения В - Өв .
Пример. Для заданной рамы (рис. 5.9) вычислить вертикальное перемещение сечения А-Vа и угол поворота сечения В - Өв . МF=-52
МF=-52  = = -26 х12
= = -26 х12 М F = -62 y1
М F = -62 y1 

 (рис. 5.11). Полученную эпюру
(рис. 5.11). Полученную эпюру 


 (рис. 5.12).
(рис. 5.12).









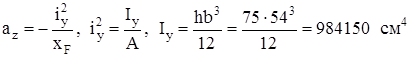

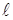 = 2,9 м, σт = 240 МПа, [σ] = 160 МПа = 16 кН/см2, Е=2·105МПа, а = 310МПа, b = 1,14МПа.
= 2,9 м, σт = 240 МПа, [σ] = 160 МПа = 16 кН/см2, Е=2·105МПа, а = 310МПа, b = 1,14МПа. ,
, ,
,
 а) первое приближение расчета:
а) первое приближение расчета: см2
см2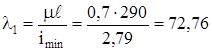











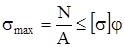


 А = 34,8 см2
А = 34,8 см2
 · 34,8
· 34,8