
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр силовых факторов для балок и рам.
Для заданных схем балок и рам (рис. 1.13, 1.14) построить эпюры внутренних усилий. Данные для размеров и нагрузок выбрать из таблицы 1 соответственно своему шифру.
Рисунок 1.13
Продолжение рисунка 1.13
Рисунок 1.14
Продолжение рисунка 1.14 Таблица 1
Тема 2. Определение геометрических характеристик плоского сечения
Рассмотрим основные геометрические характеристики. К ним относятся: а) статические моменты площади Sz, Sy и ее центр тяжести; б) осевые моменты инерции Iz, Iу; в) центробежный момент инерции Izy. Поскольку поперечное сечение это сложная фигура, то для определения геометрических характеристик она разбивается на простые геометрические фигуры. После этого произвольно выбираем оси z и у. Координаты центра тяжести Yц.т., Zц.т.. заданного сечения определяются на основании таких формул:
где А – площадь простой фигуры; Sy, Sz – статические моменты площади каждой фигуры относительно произвольно избранных осей z и у. После определения координат центра тяжести проводят центральные оси заданного сложного сечения и определяют относительно этих осей осевые и центробежный моменты инерции, используя для этого следующие формулы: 1 Для осевых моментов инерции: Iz = Iy = где Для прямоугольника: А – площадь простой фигуры. а, b – соответственно расстоянию от центра тяжести данной фигуры к оси, которая проходит через центр тяжести всей фигуры (Zц.т.., Уц.т..) 2 Для центробежного момента инерции: Izy =
При вычислении центробежного момента инерции необходимо учитывать знаки отрезков а и b.
Положение главных осей инерции сечения определяется на основании формулы:
Если a0 положительное, то угол откладывают против часовой стрелки. КОНТРОЛЬНОЕ ЗАДАНИЕ №2 Определение геометрических характеристик плоского сечения
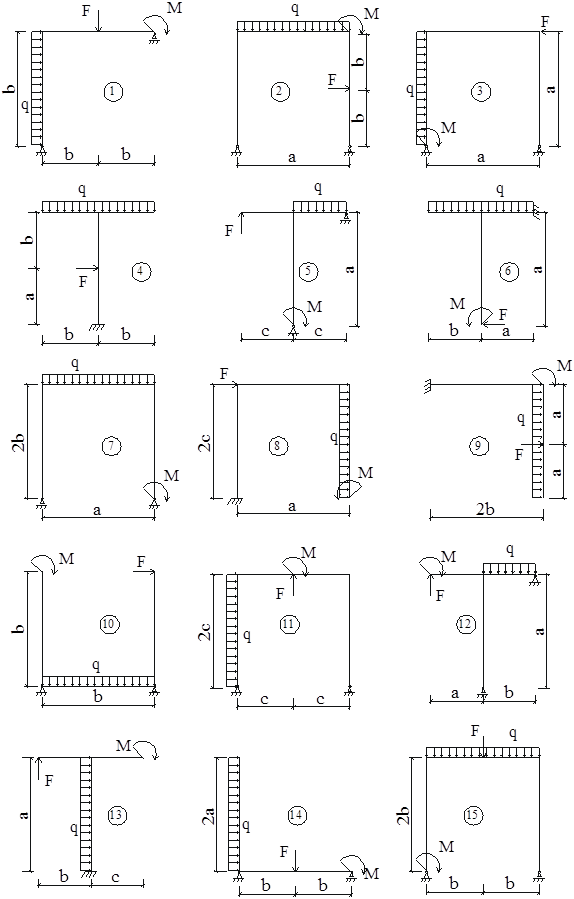
5 Для заданных схем сечения (рис.2.2) с размерами, которые следует взять из таблицы 2, соответственно собственному шифру, определить положение центральных осей фигуры, вычислить осевой и центробежный моменты инерции и определить положение главных осей.
Таблица 2
Рисунок 2.2 Пример: Определить геометрические характеристики плоского сечения (рис.2.3) и положение главных осей инерции: zгл, угл.
1 Выбираем произвольные оси Z, Y. 2 Определяем координаты центра тяжести сечения: Уц.т. = 7.4 см. Zц.т. = 2.4 см. 3 Вычисляем моменты инерции относительно осей центра тяжести сечения:
а) осевые Iz = Iy = б) центробежный Izy = 4 Определяем положение главных осей инерции: zгл, угл. tq2a0== 2a0 = + 280 41¢ a0 = + 14020¢
Знак плюс означает, что угол a0 нужно отложить против часовой стрелки.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.199.243 (0.007 с.) |

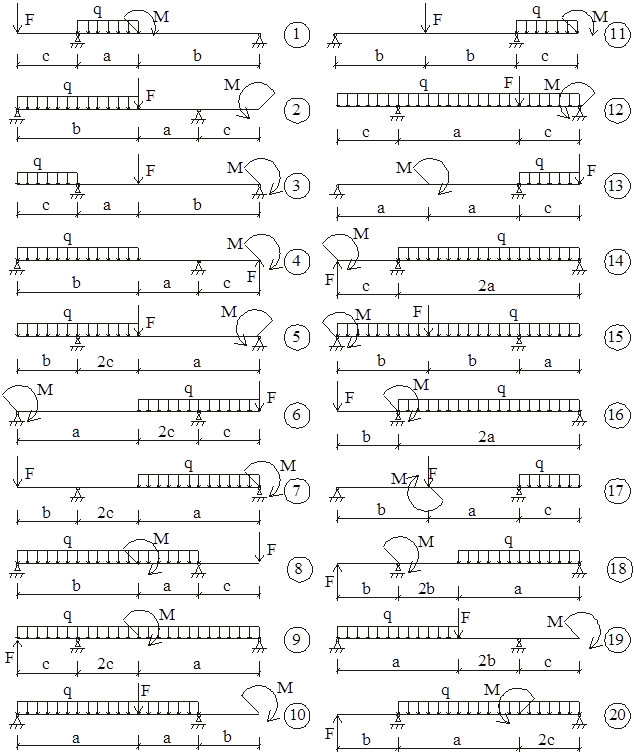

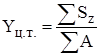 ;
; 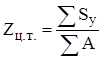 ,
,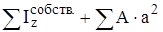 ,
,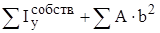 ,
,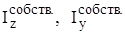 – моменты инерции относительно собственных центральных осей простой фигуры.
– моменты инерции относительно собственных центральных осей простой фигуры. (рис.2.1)
(рис.2.1)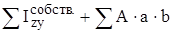 ,
, где А, а, b – то же, что в предыдущих формулах, а
где А, а, b – то же, что в предыдущих формулах, а 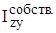 =0, поскольку собственные оси простой фигуры являются главными осями инерции, а относительно главных осей инерции центробежный момент всегда равняется нулю.
=0, поскольку собственные оси простой фигуры являются главными осями инерции, а относительно главных осей инерции центробежный момент всегда равняется нулю.

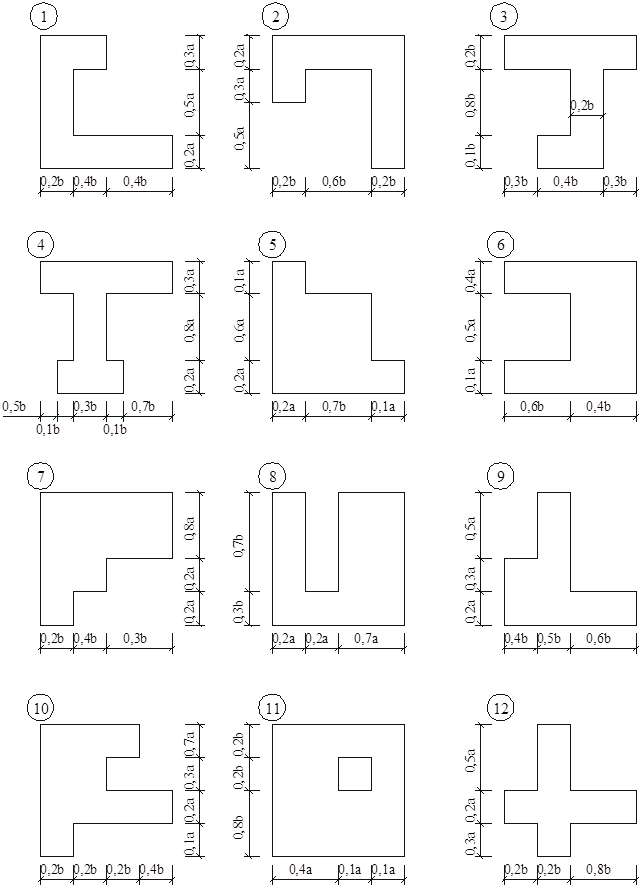
 Разбиваем данную фигуру на простые.
Разбиваем данную фигуру на простые.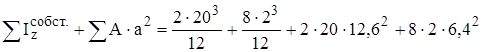 = 2264.42 см4.
= 2264.42 см4. = 384.42 см4.
= 384.42 см4.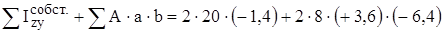 = - 514.24 см4.
= - 514.24 см4.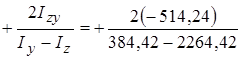 = +0,5471
= +0,5471


