Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы выполнения курсового проектаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ЦЕЛЬ КУРСОВОГО ПРОЕКТА Курсовой проект является завершающим этапом в изучении дисциплины «Основы расчета и проектирования измерительных механизмов» и представляет собой самостоятельную работу студента. Основной целью выполнения курсового проекта является приобретение студентами практических навыков в разработке структурных схем измерительных механизмов, расчета основных деталей и их проектирование. В результате изучения дисциплины «Основы расчета и проектирования измерительных механизмов» необходимо сформировать у студента следующие профильно-специализированные компетенции: ПСК1. Готов участвовать в разработке и реализации технологических процессов обработки и контроля деталей машин и механизмов в процессе обучения рабочего в области технического регулирования соответствующего квалификационного уровня. ПСК 2. Способен участвовать в практическом освоении систем управления качеством на предприятии и в образовательном учреждении. ПСКЗ. Способен участвовать в выполнении заданий по разработке, пересмотру, актуализации и применению нормативных документов в сфере технического регулирования и управления качеством в процессе обучения рабочего соответствующего квалификационного уровня. ПСК4. Готов выполнять работы по метрологическому обеспечению производства и образовательного учреждения. ПСК5. Готов выполнять работы, связанные с проектированием деталей и узлов механизмов. При выполнении курсового проекта по дисциплине «Основы расчета и проектирования измерительных механизмов» студент должен: Знать: – основную номенклатуру механизмов; – современные методы проектирования типовых деталей машиностроения; – основные понятия и положения структурного анализа типовых механизмов; – основы проектирования рычажных, винтовых, зубчатых механизмов. Уметь: – выбирать структурные схемы измерения; – конструировать основные структурные схемы для измерительных устройств; – рассчитывать основные размеры типовых деталей; – организовывать работу малых коллективов исполнителей. Владеть: – современными методами расчета и проектирования измерительных механизмов.
СОДЕРЖАНИЕ КУРСОВОГО ПРОЕКТА В соответствии с заданием студент проектирует конкретные механизмы. Курсовой проект состоит из пояснительной записки и графической части. Пояснительная записка должна содержать обоснование, ход работы, расчеты (проектировочные и прочностные). В графической части проекта, состоящей из двух листов формата А1, изображается: 1-ый лист – рычажный механизм; 2-ой лист – зубчатый механизм. Конструкторская документация должна быть выполнена в соответствии с ЕСКД.
ЭТАПЫ ВЫПОЛНЕНИЯ КУРСОВОГО ПРОЕКТА Выполнять курсовую работу рекомендуется последовательно по этапам: 1. Спроектировать рычажный механизм; 2. Спроектировать зубчатый механизм; 3. Рассчитать передачу винт-гайка скольжения. Рисунок 3 – Кривошипно–ползунный механизм Кулисные механизмы (рис. 4) служат для преобразования равномерно–вращательного движения кривошипа в качательное движение кулисы или неравномерное прямолинейное колебательное (возвратно–поступательное) движение ползуна. Кулисные механизмы используются в строгальных станках, когда рабочий ход (снятие стружки) происходит медленно, а нерабочий ход (возвращение резца) – быстро.
Рисунок 4 – Кулисный механизм
На рисунке 5 показана схема кулисного механизма с входным поршнем на шатуне. Такая схема используется в механизмах гидронасосов ротационного типа с вращающимися лопастями, а также в различных гидро– или пневмоприводах механизма с входным поршнем 3 на шатуне, скользящем в качающемся (или вращающемся) цилиндре [1].
Рисунок 5 – Кулисный механизм: 1 – кривошип; 2 – шатун; 3 – поршень Расчет погрешности В некоторых измерительных головках передаточный механизм содержит в себе рычажные передачи. Важной особенностью рычажных передач, используемых в измерительных средствах, является то, что контакт между сопрягаемыми элементами рычажной передачи делается скользящим. Наилучшая форма контакта — в виде сферы и плоскости, так как в этих случаях контакт теоретически осуществляется в точке, и эти поверхности относительно просто изготовить. При этом оказывается, что точность передачи зависит от того, на каком элементе передачи будет установлена плоскость, а на каком сфера и как эти плоскость и сфера расположены относительно опоры вращения. Сфера может быть установлена либо на звене, совершающем поступательное движение, либо на звене с вращательным движением (рис. 6). Для обоих этих рычагов теоретическая величина перемещений конца рычага sT при малых углах поворота равна длине рычага, умноженной на угол поворота, т. е. sT=lφ. На рис. 6(а), у рычажной передачи величина перемещения s = l*sinφ. Поэтому за механизмами, у которых сфера расположена на звене, совершающем вращательное движение, установилось название синусные передачи, а за рычагами, у которых на конце находится сфера — синусные рычаги. На рис. 6(б), у рычажной передачи сфера находится на звене, совершающем поступательное движение. Величина перемещения s = l tgφ. За такими механизмами, у которых сфера расположена на звене, совершающем поступательное движение, установилось название тангенсных механизмов, а за рычагами, у которых рабочей поверхностью является плоскость, тангенсных рычагов. Обычно в передаточных механизмах используются и синусные, и тангенсные рычаги (на рис. 6(в) рычаги 1 и 3 — синусные, а рычаг 2 – тангенсальный). Погрешность синусных рычагов. Для определения значения расчетной погрешности рычажной передачи заменим я sin ϕ формулой разложения этой тригонометрической функции в степенной ряд по углу ϕ и ограничимся членами со степенью аргумента ϕ не выше третьей:
Тогда вместо s=l Sinϕ можно написать:
Погрешность перемещения синусного рычага будет равна разности между теоретическим перемещением sT и расчетным s, т. е.
Таким образом, синусные рычаги имеют систематическую (функциональную) погрешность со знаком плюс, которая зависит от длины рычага и угла поворота. Погрешность тангенсных рычагов. Используя тот же прием, получим:
Погрешность тангенсных рычагов имеет минусовый знак и также зависит от угла поворота и длины исходного рычага. Выявленные погрешности часто называют погрешностями схемы (схемные погрешности), и они носят расчетный характер без учета погрешности изготовления. Сопоставление погрешностей синусного и тангенсного рычагов и общие рекомендации по их применению: 1. Погрешность синусных рычагов проявляется со знаком плюс (т. е. расчетные перемещения больше теоретических), а погрешности тангенсных рычагов — со знаком минус. 2. Погрешности синусного рычага в два раза меньше, чем тангенсного, при одинаковых начальных длинах рычагов и равных углах поворота. 3. При последовательной установке обоих видов рычагов можно произвести взаимную компенсацию погрешностей при соответствующей регулировке длин плеч рычагов, что и используют в рычажно-зубчатых головках. 4. Регулировкой плеч рычагов (практически это можно осуществить изменением положения сферы) можно компенсировать расчетную погрешность. 5. Зазоры в направляющих с поступательным перемещением практически не отражаются на погрешностях передачи при синусном рычаге, но проявляются значительной величиной при тангенсных рычагах (увеличивается случайная погрешность). При конструировании рычажной передачи необходимо, чтобы центр сферы располагался на прямой, проходящей через центр опоры и в исходном положении эта прямая была перпендикулярна линии перемещения поступательного звена. Если используется прямолинейный рычаг, на втором конце которого находится также сфера, то все центры сфер должны располагаться на одной линии. Если используется угловой рычаг, то центры сфер должны быть расположены в исходном положении на концах угла с вершиной на оси вращения, который должен быть дополнительным к углу между линиями измерения элементов, совершающих прямолинейное движение [4].
Рисунок 7 – Основные параметры зубчатого колеса
Значение модуля m определяется по ГОСТ 9563 – 60. Окружность, модуль по которой равен стандартному, называется делительной. Высота головки зуба ha = ra – r. Высота ножки зуба hf = r – rf. Зацепление зубчатых колес в передаче требует соблюдения основного условия – равенства окружных шагов ведущего и ведомого зубчатых колес:
так как Передаточное отношение зубчатой передачи равно отношению числа зубьев ведущего колеса к числу зубьев ведомого колеса [6]:
Единственной измерительной головкой, имеющей механизм увеличивающего устройства в виде только зубчатых передач, является индикатор часового типа.
Рисунок 8 – Индикатор часового типа: а – схема; б – конструкция индикатора ИЧ–10
Схема индикатора (рис. 8, а) состоит из рейки 1, которая нарезана на измерительном стержне, имеющем измерительный наконечник 2, зацепляющейся с трибом 3 (трибом называют обычно зубчатое колесо малого модуля с небольшим числом зубьев 6–16, чаще всего изготовленное за одно со своей осью, так называемое «валковое колесо»). На одной оси с трибом установлено зубчатое колесо 4 большего диаметра, находящееся в зацеплении с трибом 5, на оси которого установлена основная стрелка 6.С помощью стрелки по шкале 7 отсчитывают перемещения измерительного наконечника 2 [4]. Рисунок 9 – Зубчатое зацепление
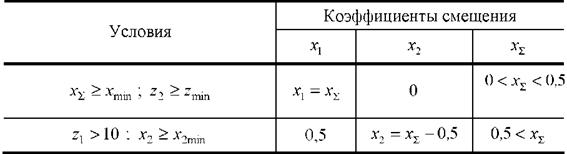
Отрицательная зубчатая передача составляется из двух отрицательных зубчатых колёс, из одного отрицательного и другого нулевого или из одного отрицательного и другого положительного. В последнем случае коэффициент смещения отрицательного зубчатого колеса должен быть по абсолютной величине больше, чем положительного. Делительные окружности зубчатой передачи пересекаются (рис. 9, в). Радиусы делительных окружностей больше радиусов начальных окружностей (r > rw); межосевое расстояние определяется по той же формуле, что и для положительной передачи. Для отрицательной передачи aw < a и aw < a. При проектировании следует учитывать особенности каждого вида передач. Наилучшими качествами обладают положительные зубчатые передачи вследствие того, что у них больше радиусы кривизны боковых поверхностей зубьев. Кроме того, при тех же значениях передаточного числа и модуля они имеют меньшие габариты и вес. Нулевые передачи имеют худшие эксплуатационные качества, чем положительные. Однако в настоящее время они наиболее часто применяются в машинах, так как очень просто рассчитываются и удовлетворяют принципу сменности колёс. Самые плохие эксплуатационные качества имеет отрицательная передача. Согласно ГОСТ 16532 – 70 зубчатая передача, у которой оба зубчатых колеса нулевые, называется зубчатой передачей без смещения, а зубчатая передача, у которой хотя бы одно колесо изготовлено со смещением, называется зубчатой передачей со смещением. Два любых зубчатых колеса, изготовленные одной и той же инструментальной рейкой, могут образовать правильное плотное зубчатое зацепление, т.е. зацепление без боковых зазоров между зубьями. В беззазорном зацеплении как рабочие, так и нерабочие стороны зубьев находятся в контакте одновременно. При этом толщина зуба (Sw) по дуге начальной окружности одного колеса должна быть равна ширине впадины (ew) по дуге начальной окружности второго и наоборот: Sw1 = ew2 (11) Sw2 = ew1 (12) Основными величинами, характеризующими зацепление зубчатых колес являются: aw - угол зацепления; xS = x1 + x2 - суммарный коэффициент смещения; у- коэффициент воспринимаемого смещения; a - делительное межосевое расстояние. В общем случае, в зависимости от значений указанных величин зубчатые зацепления классифицируются следующим образом: 1) номинальное зацепление (aw = a, x1 = x2 = 0, aw = a, y = 0); 2) равносмещённое зацепление (aw = a, x1 = -x2, aw = a, y = 0); 3) неравносмещённое зацепление (aw ≠ a, xS ≠ 0, aw ≠ a, y > 0). Формулы для указанных зацеплений даны в таблице 2. Нарезая зубчатые колёса с различным смещением, можно получить зубчатую передачу с необходимыми свойствами. Не всегда удается спроектировать зубчатый механизм, отвечающий требованиям конструкции при стандартном модуле (m). Для оценки спроектированной зубчатой передачи приняты следующие качественные показатели: коэффициент удельного давления q, характеризующий влияние геометрических параметров на контактную прочность и выкрашивание зубьев; коэффициент перекрытия e, показывающий характер нагружения зубьев; коэффициент относительного скольжения X, определяющий влияние геометрических параметров на износ зубьев и заедание; коэффициент формы зуба у, характеризующий изгибную прочность зубьев. Все эти качественные показатели являются функцией выбираемых коэффициентов смещения. Увеличивая коэффициенты смещения каждого колеса и их суммы, можно повысить контактную прочность передачи, так как при этом уменьшаются коэффициенты удельного давления; повысить износостойкость колёс и уменьшить их склонность к заеданию, так как уменьшаются коэффициенты скольжения; увеличить изгибную прочность зубьев, так как увеличивается коэффициент формы зуба. Но, с другой стороны, с увеличением коэффициентов смещения уменьшается коэффициент перекрытия. Выбирая расчётные коэффициенты смещения, следует учитывать конкретные условия работы проектируемой зубчатой передачи: её быстроходность, изменяемость или цикличность нагрузки, условия смазки и т.д. Таблица 2 - Формулы для расчета параметров зацеплений зубчатых колес
Продолжение таблицы 2
Однако расчётные коэффициенты смещения любой зубчатой передачи прежде всего должны обеспечить отсутствие заклинивания, подреза и заострения зубьев, а также гарантировать минимально допустимую величину коэффициента перекрытия. В общем случае при изготовлении колёс (z1) и (z2) со сдвигом режущего инструмента x1 ≠ 0; x2 ≠0; x1 + x2 ≠0 монтажный угол зацепления не равен профильному углу исходного контура (aw ≠ a).
Монтажный угол зацепления определяется из зависимости:
(13) где y – коэффициент воспринимаемого смещения: Величина суммарного коэффициента коррекции зацепления связана с величиной угла зацепления
где inva = tga - a - эвольвентная функция.
Полученная величина xS может быть распределена между колёсами в общем случае произвольно. Однако с целью повышения сопротивляемости рабочих поверхностей заеданию и контактному разрушение рекомендуется значения этих коэффициентов выбирать по зависимостям:
(15) Если габариты зубчатой передачи не ограничиваются величиной am, то коэффициенты коррекции назначаются из соображений повышения эксплуатационных показателей зубчатых колёс. Одним из таких показателей является отсутствие подрезания и заострения зубьев.
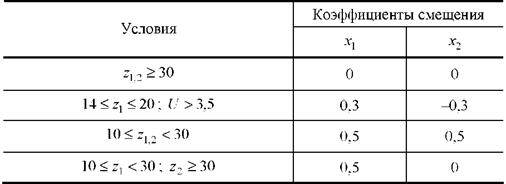
Для устранения подрезания зубьев при изготовлении колёс режущий инструмент сдвигают на величину + xm, где z – число зубьев исправляемого колеса. (16) При большом положительном сдвиге режущего инструмента возможно пересечение эвольвент, образующих рабочие профили. Это явление называется заострением зуба (рис. 10). Для стандартного исходного контура предельное значение коэффициента смещения, превышение которого при изготовлении приводит к заострению зубьев, определяется из зависимости: x.3 = 0,5z.
Рисунок 10 – Заострение зуба Для любого исходного контура может быть применена зависимость:
(17) где
Таким образом, назначаемые коэффициенты смещения должны выбираться из диапазона значений хп < х < хз. Существуют несколько систем коррекции, обеспечивающих определенные свойства зацепления, а именно: отсутствие подрезания зубьев, обеспечение заданного межцентрового расстояния, повышенной контактной прочности зубьев и повышенной износостойкости. При инженерных расчётах можно воспользоваться рекомендациями табл. 3 и 4 [7].
Таблица 3 - Свободный выбор межосевого расстояния
Таблица 4 – Вписывание в заданное межосевое расстояние
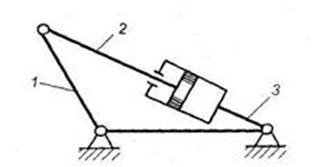
3.2.2. Порядок построения зубчатого зацепления По вычисленным параметрам проектируемая зубчатая передача строится следующим образом: 1. Провести осевую линию и на ней выбрать центры колес О1 и О2, полюс зацепления Р (точка касания начальных окружностей), т.е. О1Р +О2Р = aω = rω1 + rω2 , (19) где aω – межосевое расстояние ; rω1 и rω2 – соответственно радиус начальной окружности шестерни и колеса. 2. Провести делительные и основные окружности радиусами r1, 2 и r b1,2. 3. Построить теоретическую линию зацепления как касательную к основным окружностям, проходящую через полюс зацепления Р-АВ. 4. Построить эвольвенты зубьев 1-го и 2-го колес. Построение эвольвенты 1-го колеса: - на основной окружности от точки А провести дугу ᴗ АР ʹ, равную длине отрезка АР; - разделить прямую АР и дугу ᴗ АР ʹ на четыре равные части. На прямой получаются точки Р, 1, 2, 3, 4, а на дуге – точки Р ʹ, 1 ʹ, 2 ʹ, 3 ʹ, 4 ʹ. При этом 1Р = ᴗ1 ʹ Р ʹ; 12 = ᴗ1 ʹ 2 ʹ и т.д.; - такие же отрезки деления откладываются по другую сторону от точки А. На прямой отмечаются точки 5, 6, 7, 8…, на дуге – точки 5 ʹ, 6ʹ, 7ʹ, 8ʹ…; - к радиусам О1 – 1ʹ, О1 – 2ʹ и т.д. в сторону полюса восстановить перпендикуляры, на которых отложить отрезки 1ʹ1ʹʹ = 1Р, 2ʹ2ʹʹ = 2Р и т.д. - точки Рʹ, 1ʹʹ, 2, 3ʹʹ, 4ʹʹ, 5ʹʹ, 6ʹʹ, 7ʹʹ, 8ʹʹ соединяем лекальной кривой. Построенную эвольвенту ограничиваем по высоте зуба в точке пересечения эвольвенты с окружностью вершин зубьев (ra1); - выделить практическую часть линии зацепления ab (пересечение окружностей вершин с теоретической линией зацепления). Аналогично строится эвольвента зубьев 2-го колеса. 5. Построить ножку зуба. Профиль ножки зуба колеса состоит из эвольвентной части и переходной кривой (галтели), которая соединяет эвольвентную часть с окружностью впадин. На практике пользуются упрощенным методом построения, для чего: - проводим окружности впадин для 1-го и 2-го колес соответствующими радиусами rf1 и rf2; - от точек пересечения эвольвенты с основными окружностями в направлении О1 и О2 проводим радиальные прямые; - строим сопряжение этих радиальных прямых с окружностями впадин радиусом r = 0,2 m.
Рисунок 11 – Зубчатое зацепление
6. Построить полный зуб, для чего: - по дуге делительной окружности (от точки пересечения эвольвенты с делительной окружностью) отложить толщину зуба, определяемую по формуле - провести оси симметрии зубьев и построить полные зубья (с левым и правым профилями) первого и второго зубчатых колес, используя шаблон.
Рисунок 12 – Определение активной части линии зацепления
Так как ab= ε pb, то будем иметь:
Ak = lb = ε pb – pb = (ε – 1) pb; kl = (2 – ε) pb. (21)
На участках ak и lb происходит одновременное зацепление двух пар профилей. 2. Коэффициент относительного скольжения зубьев. Профили, находящиеся во взаимном зацеплении, называются сопряженными (рис. 11). Пусть эти профили касаются в точке с, лежащей на образующей прямой А. Выберем на этих профилях точки m1, m2, лежащие на начальных окружностях. Отрезок сm1 профиля 1 и отрезок сm2 профиля 2 не равны между собой. В процессе зацепления профилей наблюдается не только качение, но и скольжение профиля по профилю. В самом деле, при движении точек m1 и m2 к полюсу, они проходят равные пути m1Р и m2Р. Одновременно с этим дуга сm2 перемещается по дуге сm1. Так как эти дуги не равны, то качение профилей сопровождается скольжением. Скольжение профилей влияет на износ зубьев, уменьшая тем самым и износостойкость зубчатых передач. Для оценки взаимного скольжения профилей зубьев пользуются коэффициентом скольжения, величину которого можно рассчитать по аналитическим зависимостям:
где р1+р2 = АВ – теоретическая линия зацепления; р1, р2 – радиусы кривизны сопряженных профилей; λ – коэффициент относительного скольжения, изменяется в пределах от +1 (на головке зуба) до -∞ (на ножке зуба), (рис. 11); U – передаточные функции.
В полюсе
3. Коэффициент удельного давления. Взаимодействие двух прямых зубьев, передающих нагрузку, сопровождается смятием поверхностей этих зубьев в зоне касания. Если эвольвентные поверхности зубьев условно принять за поверхности круглых цилиндров, радиусы которых равны радиусам кривизны эвольвентных поверхностей в точке их касания, то для определения возникающего при этом наибольшего, удельного давления (напряжения смятия) можно будет условно использовать известную формулу Герца.
Чтобы охарактеризовать влияние геометрической формы зуба на удельное давление σсм, независимо от величины модуля, установим понятие о коэффициенте удельного давления как об отношении модуля к приведенному радиусу кривизны, обозначив его величину буквой q.
Коэффициент q характеризует взаимодействие двух зубьев у колес передачи одновременно. В общем виде будем иметь:
где р1 и р2 – радиусы кривизны профилей зубьев в точке зацепления. На рисунке 11 представлена диаграмма изменения коэффициента q в зависимости от радиуса кривизны р. Из рисунка видно, что р1 + р2 = АВ = е. В середине теоретической линии зацепления коэффициент q имеет минимальное значение:
При расчете зубьев на прочность большое значение имеет коэффициент qp в полюсе зацепления:
где zΣ = z1 + z2 [8].
Рисунок 14 – Расчет передачи винт-гайка на износостойкость
Расчет передачи на износостойкость ведут из условия невыдавливания смазочного материала, предполагая, что вследствие приработки нагрузка по виткам резьбы распределяется равномерно:
где Fa – внешняя осевая сила; А – площадь рабочей поверхности витка; d2 – средний диаметр резьбы; Н1 – рабочая высота профиля резьбы; zb – число витков в гайке высотой Н: Таблица 5 - Допускаемое давление в резьбе для пары винт-гайка
Примечание. При редкой работе, а также для гаек малой высоты значение
Для проектного расчета полученную формулу целесообразно преобразовать, заменив Тогда (рис.14):
Принимают После расчета резьбы сильно нагруженные винты, например винты домкратов, проверяют на прочность, принимая Пример расчета передачи винт-гайка скольжения Рассчитать винт домкрата, а так же определить его КПД. Резьба самотормозящая упорная грузоподъемность F а = 150 кН, l = 1,0 м, винт – сталь 35, гайка – чугун, подпятник – шариковый. Решение. 1.определим диаметр винта из условия износостойкости, приняв
(
2.по таблицам стандарта выбираем резьбу М 85х12: d = 85 мм, р = 12 мм шаг резьбы d 1 = 64,2 мм, d 2 = 76 мм, h = 9 мм (коэффициенты резьбы), коэффициент трения ¦ = 0,1 Угол подъема резьбы
3. Число витков:
4.Для домкрата (при наличии слабой смазки в винте ¦ = 0,1)
Рекомендуемая литература Основная 1. Теория механизмов и механика машин: Учеб. для вузов / К. В. Фролов, С. А. Попов, А. К. Мусатов и др.; Под ред. К. В. Фролова. – 5-е изд., стереотип. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2010. – 664 с.: ил. 2. Теория механизмов и машин. Курсовое проектирование: учеб. пособие для вузов / под ред. Г. А. Тимофеева и Н. В. Умнова. - –.: Изд-во МГТУ им. Н. Э. Баумана, 2010. – 154 с.: ил. 3. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин: учеб. для вузов / Под общ. ред. д. т. н., проф. Н. В. Гулиа. – 2-е изд., испр. – СПб.: Изд-во «Лань», 2010. – 416 с.: ил.
Дополнительная 4. Детали машин. Электронный учебный курс для студентов очной и заочной форм обучения. Составитель: к.т.н., доцент кафедры теоретической и прикладной механики Каримов Ильдар. Режим доступа: http://www.detalmach.ru/ 5. Дунаев П.Ф. конструирование узлов и деталей машин: учеб.пособие для студ.высш.учеб.заведений /Дунаев П.Ф, Леликов О.П. – 9-е изд., перераб. И доп. – М.: Издательский центр «Академия», 2006. – 496 с. 6. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин: учеб. для вузов / Под общ. ред. д. т. н., проф. Н. В. Гулиа. – 2-е изд., испр. – СПб.: Изд-во «Лань», 2010. – 416 с.: ил. 7. Прикладная механика. Электронный учебный курс для студентов очной и заочной форм обучения. Составитель: к.т.н., доцент кафедры теоретической и прикладной механики Каримов Ильдар. 8. Методические указания для выполнения курсового проекта по дисциплине «Теория механизмов и машин» Структурный и кинематический анализ (ГОС – 2000). Екатеринбург, ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2010. 36 с. 9. Марков Н.Н., Ганевский Г.М. Конструкция, расчет и эксплуатация измерительных инструментов и приборов: Учебник для техникумов по специальности «Производство контрольно-измерительных инструментов и приборов». – 2-е изд., перераб. и Доп. – М.: Машиностроение, 1993. – 416 с.: ил. 10. ТММ. Проектирование и анализ зубчатых механизмов: метод. указ. / сост.: П. А. Галкин, Л. Х. Никитина. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2008. - –2 с. Режим доступа: http://www.prikladmeh.ru
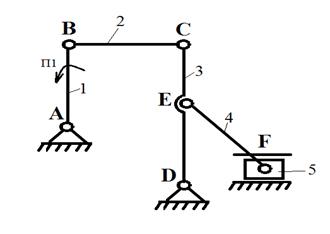
ПРИЛОЖЕНИЕ А Варианты заданий для проектирования рычажного механизма
Вариант 1
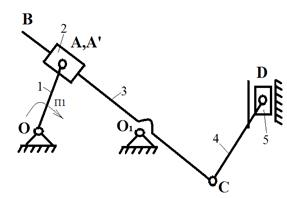
Вариант 2
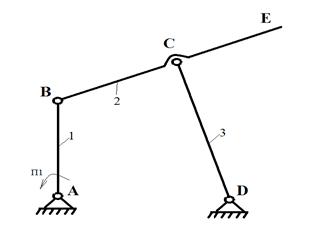
Вариант 3
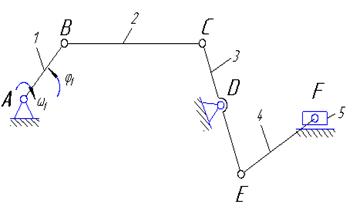
Вариант 4
Вариант 5
ПРИЛОЖЕНИЕ Б Варианты заданий для проектирования зубчатого механизма Таблица 7 – Исходные данные
ПРИЛОЖЕНИЕ В Варианты заданий для расчета передачи винт-гайка скольжения
Рассчитать винт домкрата, а так же определить его КПД. Резьба самотормозящая упорная грузоподъемность F а, кН, l, м, подпятник – шариковый. Исходные данные приведены в таблице 8.
Таблица 8 – Исходные данные
ПРИЛОЖЕНИЕ Г Пример выполнения Листа №1 «Проектирование рычажного механизма»
ПРИЛОЖЕНИЕ Д Пример выполнения Листа №2 «Проектирование зубчатого механизма»
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОГО ПРОЕКТА ПО ДИСЦИПЛИНЕ «ОСНОВЫ РАСЧЕТА И ПРОЕКТИРОВАНИЯ ИЗМЕРИТЕЛЬНЫХ МЕХАНИЗМОВ»
Подписано в печать. Формат 60×84/16. Бумага для множ. аппаратов. Печать плоская. Усл. Печ. л.. Уч.-изд. л.. Тираж экз. Заказ №. ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, ул. Машиностроителей, 11. а
Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11. ЦЕЛЬ КУРСОВОГО ПРОЕКТА Курсовой проект является завершающим этапом в изучении дисциплины «Основы расчета и проектирования измерительных механизмов» и представляет собой самостоятельную работу студента. Основной целью выполнения курсового проекта является приобретение студентами практических навыков в разработке структурных схем измерительных механизмов, расчета основных деталей и их проектирование. В результате изучения дисциплины «Основы расчета и проектирования измерительных механизмов» необходимо сформировать у студента следующие профильно-специализированные компетенции: ПСК1. Готов участвовать в разработке и реализации технологических процессов обработки и контроля деталей машин и механизмов в процессе обучения рабочего в области технического регулирования соответствующего квалификационного уровня. ПСК 2. Способен участвовать в практическом освоении систем управления качеством на предприятии и в образовательном учреждении. ПСКЗ. Способен участвовать в выполнении заданий по разработке, пересмотру, актуализации и применению нормативных документов в сфере технического регулирования
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |


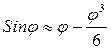 (3)
(3)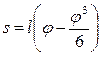 (4)
(4) (5)
(5)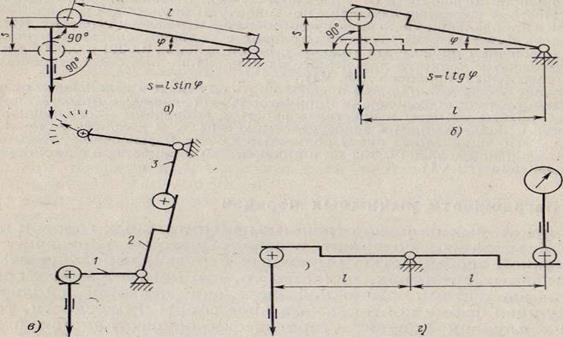 Рисунок 6 – Схемы рычажных механизмов:
а — синусного; б — тангенсного; в — двухрычажная передача с угловым рычагом; г — двухрычажная передача со сферическими опорами на одной прямой
Рисунок 6 – Схемы рычажных механизмов:
а — синусного; б — тангенсного; в — двухрычажная передача с угловым рычагом; г — двухрычажная передача со сферическими опорами на одной прямой
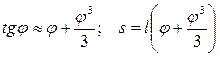 (6)
(6)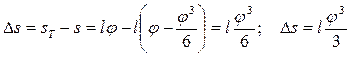 (7)
(7) (8)
(8) , то и
, то и 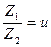 .
.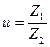 (9)
(9)




 (14)
(14)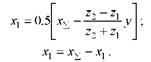
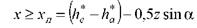


 (18)
(18)

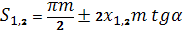 ; и толщину впадины, определяемую по формуле:
; и толщину впадины, определяемую по формуле:  ;
;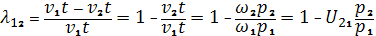 ; (22)
; (22)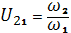 или
или  ; (23)
; (23)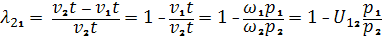 , (24)
, (24)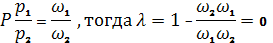
 , (25)
, (25)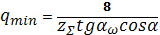 . (26)
. (26)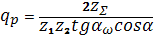 , (27)
, (27)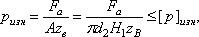 , (29)
, (29)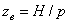 (здесь р — шаг резьбы);
(здесь р — шаг резьбы); 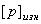 - допускаемое давление (выбирается по табл. 5).
- допускаемое давление (выбирается по табл. 5).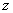 на
на 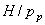 , обозначив
, обозначив 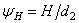 — коэффициент высоты гайки,
— коэффициент высоты гайки, 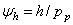 — коэффициент высоты резьбы.
— коэффициент высоты резьбы.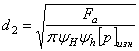 (30)
(30) для трапецеидальной и
для трапецеидальной и 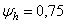 для упорной резьбы;
для упорной резьбы; 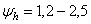 в зависимости от конструктивных соображений (большие значения для резьб меньших диаметров). Полученное значение d 2согласуется со стандартом.
в зависимости от конструктивных соображений (большие значения для резьб меньших диаметров). Полученное значение d 2согласуется со стандартом.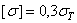 , и на устойчивость.
, и на устойчивость.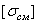 =6 МПа,
=6 МПа, 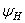 = 1,8,
= 1,8, 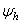 = 0,75
= 0,75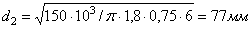

 , что обеспечивает запас самоторможения.
, что обеспечивает запас самоторможения.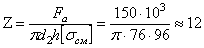
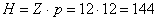 мм
мм