
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение качественных показателей зубчатого зацепления
1. Коэффициент перекрытия определяется по формуле:
где ab – активная часть линии зацепления (определяется графически); pb= πm cosα – шаг по основной окружности; α = 20о. Коэффициент перекрытия определяет количество пар зубьев, находящихся одновременно в зацеплении. Для плавной и безударной работы зубчатой пары должно быть выполнено условие непрерывности смены зубчатых профилей, т. Е. вторая пара зубчатых профилей должна войти в зацепление раньше, чем первая пара выйдет из зацепления. При проектировании зацепления коэффициент перекрытия берут равным не менее 1,1. Если, например, ε = 1,3, т.е. 1 < ε < 2, в зацеплении находятся попеременно одна или две пары профилей. При помощи коэффициента перекрытия можно определить тот участок активной части линии зацепления, на котором производится зацепление одной пары зубьев, а также зацепление двух пар профилей. Для этого откладываем от крайних точек a и b активной части линии зацепления отрезки al, bk, равные длине основного шага (pb), получаем участки ab, lb, ak и kl (рис. 12).
Рисунок 12 – Определение активной части линии зацепления
Так как ab= ε pb, то будем иметь:
Ak = lb = ε pb – pb = (ε – 1) pb; kl = (2 – ε) pb. (21)
На участках ak и lb происходит одновременное зацепление двух пар профилей. 2. Коэффициент относительного скольжения зубьев. Профили, находящиеся во взаимном зацеплении, называются сопряженными (рис. 11). Пусть эти профили касаются в точке с, лежащей на образующей прямой А. Выберем на этих профилях точки m1, m2, лежащие на начальных окружностях. Отрезок сm1 профиля 1 и отрезок сm2 профиля 2 не равны между собой. В процессе зацепления профилей наблюдается не только качение, но и скольжение профиля по профилю. В самом деле, при движении точек m1 и m2 к полюсу, они проходят равные пути m1Р и m2Р. Одновременно с этим дуга сm2 перемещается по дуге сm1. Так как эти дуги не равны, то качение профилей сопровождается скольжением. Скольжение профилей влияет на износ зубьев, уменьшая тем самым и износостойкость зубчатых передач. Для оценки взаимного скольжения профилей зубьев пользуются коэффициентом скольжения, величину которого можно рассчитать по аналитическим зависимостям:
где р1+р2 = АВ – теоретическая линия зацепления; р1, р2 – радиусы кривизны сопряженных профилей; λ – коэффициент относительного скольжения, изменяется в пределах от +1 (на головке зуба) до -∞ (на ножке зуба), (рис. 11); U – передаточные функции.
В полюсе
3. Коэффициент удельного давления. Взаимодействие двух прямых зубьев, передающих нагрузку, сопровождается смятием поверхностей этих зубьев в зоне касания. Если эвольвентные поверхности зубьев условно принять за поверхности круглых цилиндров, радиусы которых равны радиусам кривизны эвольвентных поверхностей в точке их касания, то для определения возникающего при этом наибольшего, удельного давления (напряжения смятия) можно будет условно использовать известную формулу Герца.
Чтобы охарактеризовать влияние геометрической формы зуба на удельное давление σсм, независимо от величины модуля, установим понятие о коэффициенте удельного давления как об отношении модуля к приведенному радиусу кривизны, обозначив его величину буквой q.
Коэффициент q характеризует взаимодействие двух зубьев у колес передачи одновременно. В общем виде будем иметь:
где р1 и р2 – радиусы кривизны профилей зубьев в точке зацепления. На рисунке 11 представлена диаграмма изменения коэффициента q в зависимости от радиуса кривизны р. Из рисунка видно, что р1 + р2 = АВ = е. В середине теоретической линии зацепления коэффициент q имеет минимальное значение:
При расчете зубьев на прочность большое значение имеет коэффициент qp в полюсе зацепления:
где zΣ = z1 + z2 [8].
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.007 с.) |
 , (20)
, (20)
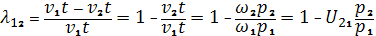 ; (22)
; (22)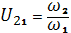 или
или  ; (23)
; (23)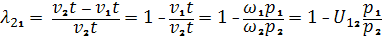 , (24)
, (24)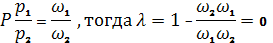
 , (25)
, (25)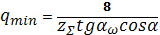 . (26)
. (26)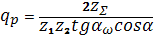 , (27)
, (27)


