
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет геометрии прямозубого эвольвентного цилиндрического зубчатого зацепления с выбором коэффициентов смещения
Рассмотрим зубчатые механизмы (передачи), составленные из колёс с прямыми зубьями. Нулевая зубчатая передача составляется из нулевых колёс (x1 = x2 = 0) или при условии x1 = -x2 (равносмещённая передача). Делительные окружности колёс нулевой зубчатой передачи касаются в полюсе Р и в процессе зацепления перекатываются друг по другу без скольжения, т.е одновременно являются и начальными окружностями колёс (рис. 9, а) rw = r = 0,5mz. Межосевое расстояние равно сумме радиусов делительных окружностей aw = r1 + r2 и называется делительным межосевым расстоянием. Угол зацепления нулевой передачи aw = a = 20°. Положительная зубчатая передача может быть составлена из двух положительных зубчатых колес x > 0 или из одного положительного и другого нулевого и, наконец, из одного положительного и другого отрицательного. В последнем случае коэффициент смещения положительного колеса по абсолютной величине должен быть больше, чем отрицательного. Делительные окружности колёс положительной зубчатой передачи не касаются друг друга, начальные окружности больше делительных, т.е rw > r, межосевое расстояние равно сумме радиусов начальных окружностей (рис. 9, б).
При этом межосевое расстояние aw > a, а угол зацепления положительной зубчатой передачи aw > a.
Рисунок 9 – Зубчатое зацепление
Отрицательная зубчатая передача составляется из двух отрицательных зубчатых колёс, из одного отрицательного и другого нулевого или из одного отрицательного и другого положительного. В последнем случае коэффициент смещения отрицательного зубчатого колеса должен быть по абсолютной величине больше, чем положительного. Делительные окружности зубчатой передачи пересекаются (рис. 9, в). Радиусы делительных окружностей больше радиусов начальных окружностей (r > rw); межосевое расстояние определяется по той же формуле, что и для положительной передачи. Для отрицательной передачи aw < a и aw < a. При проектировании следует учитывать особенности каждого вида передач. Наилучшими качествами обладают положительные зубчатые передачи вследствие того, что у них больше радиусы кривизны боковых поверхностей зубьев. Кроме того, при тех же значениях передаточного числа и модуля они имеют меньшие габариты и вес.
Нулевые передачи имеют худшие эксплуатационные качества, чем положительные. Однако в настоящее время они наиболее часто применяются в машинах, так как очень просто рассчитываются и удовлетворяют принципу сменности колёс. Самые плохие эксплуатационные качества имеет отрицательная передача. Согласно ГОСТ 16532 – 70 зубчатая передача, у которой оба зубчатых колеса нулевые, называется зубчатой передачей без смещения, а зубчатая передача, у которой хотя бы одно колесо изготовлено со смещением, называется зубчатой передачей со смещением. Два любых зубчатых колеса, изготовленные одной и той же инструментальной рейкой, могут образовать правильное плотное зубчатое зацепление, т.е. зацепление без боковых зазоров между зубьями. В беззазорном зацеплении как рабочие, так и нерабочие стороны зубьев находятся в контакте одновременно. При этом толщина зуба (Sw) по дуге начальной окружности одного колеса должна быть равна ширине впадины (ew) по дуге начальной окружности второго и наоборот: Sw1 = ew2 (11) Sw2 = ew1 (12) Основными величинами, характеризующими зацепление зубчатых колес являются: aw - угол зацепления; xS = x1 + x2 - суммарный коэффициент смещения; у- коэффициент воспринимаемого смещения; a - делительное межосевое расстояние. В общем случае, в зависимости от значений указанных величин зубчатые зацепления классифицируются следующим образом: 1) номинальное зацепление (aw = a, x1 = x2 = 0, aw = a, y = 0); 2) равносмещённое зацепление (aw = a, x1 = -x2, aw = a, y = 0); 3) неравносмещённое зацепление (aw ≠ a, xS ≠ 0, aw ≠ a, y > 0). Формулы для указанных зацеплений даны в таблице 2. Нарезая зубчатые колёса с различным смещением, можно получить зубчатую передачу с необходимыми свойствами. Не всегда удается спроектировать зубчатый механизм, отвечающий требованиям конструкции при стандартном модуле (m). Для оценки спроектированной зубчатой передачи приняты следующие качественные показатели: коэффициент удельного давления q, характеризующий влияние геометрических параметров на контактную прочность и выкрашивание зубьев; коэффициент перекрытия e, показывающий характер нагружения зубьев; коэффициент относительного скольжения X, определяющий влияние геометрических параметров на износ зубьев и заедание; коэффициент формы зуба у, характеризующий изгибную прочность зубьев.
Все эти качественные показатели являются функцией выбираемых коэффициентов смещения. Увеличивая коэффициенты смещения каждого колеса и их суммы, можно повысить контактную прочность передачи, так как при этом уменьшаются коэффициенты удельного давления; повысить износостойкость колёс и уменьшить их склонность к заеданию, так как уменьшаются коэффициенты скольжения; увеличить изгибную прочность зубьев, так как увеличивается коэффициент формы зуба. Но, с другой стороны, с увеличением коэффициентов смещения уменьшается коэффициент перекрытия. Выбирая расчётные коэффициенты смещения, следует учитывать конкретные условия работы проектируемой зубчатой передачи: её быстроходность, изменяемость или цикличность нагрузки, условия смазки и т.д. Таблица 2 - Формулы для расчета параметров зацеплений зубчатых колес
Продолжение таблицы 2
Однако расчётные коэффициенты смещения любой зубчатой передачи прежде всего должны обеспечить отсутствие заклинивания, подреза и заострения зубьев, а также гарантировать минимально допустимую величину коэффициента перекрытия. В общем случае при изготовлении колёс (z1) и (z2) со сдвигом режущего инструмента x1 ≠ 0; x2 ≠0; x1 + x2 ≠0 монтажный угол зацепления не равен профильному углу исходного контура (aw ≠ a).
Монтажный угол зацепления определяется из зависимости:
(13) где y – коэффициент воспринимаемого смещения: Величина суммарного коэффициента коррекции зацепления связана с величиной угла зацепления
где inva = tga - a - эвольвентная функция.
Полученная величина xS может быть распределена между колёсами в общем случае произвольно. Однако с целью повышения сопротивляемости рабочих поверхностей заеданию и контактному разрушение рекомендуется значения этих коэффициентов выбирать по зависимостям:
(15) Если габариты зубчатой передачи не ограничиваются величиной am, то коэффициенты коррекции назначаются из соображений повышения эксплуатационных показателей зубчатых колёс. Одним из таких показателей является отсутствие подрезания и заострения зубьев.
Для устранения подрезания зубьев при изготовлении колёс режущий инструмент сдвигают на величину + xm, где z – число зубьев исправляемого колеса. (16) При большом положительном сдвиге режущего инструмента возможно пересечение эвольвент, образующих рабочие профили. Это явление называется заострением зуба (рис. 10). Для стандартного исходного контура предельное значение коэффициента смещения, превышение которого при изготовлении приводит к заострению зубьев, определяется из зависимости: x.3 = 0,5z.
Рисунок 10 – Заострение зуба Для любого исходного контура может быть применена зависимость:
(17) где
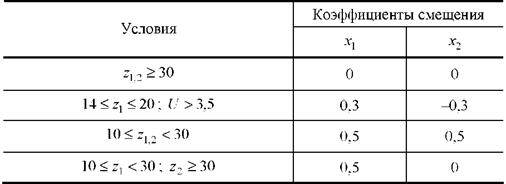
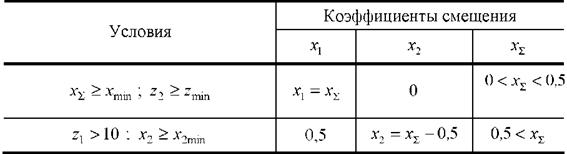
Таким образом, назначаемые коэффициенты смещения должны выбираться из диапазона значений хп < х < хз. Существуют несколько систем коррекции, обеспечивающих определенные свойства зацепления, а именно: отсутствие подрезания зубьев, обеспечение заданного межцентрового расстояния, повышенной контактной прочности зубьев и повышенной износостойкости. При инженерных расчётах можно воспользоваться рекомендациями табл. 3 и 4 [7].
Таблица 3 - Свободный выбор межосевого расстояния
Таблица 4 – Вписывание в заданное межосевое расстояние
3.2.2. Порядок построения зубчатого зацепления По вычисленным параметрам проектируемая зубчатая передача строится следующим образом: 1. Провести осевую линию и на ней выбрать центры колес О1 и О2, полюс зацепления Р (точка касания начальных окружностей), т.е. О1Р +О2Р = aω = rω1 + rω2 , (19) где aω – межосевое расстояние ; rω1 и rω2 – соответственно радиус начальной окружности шестерни и колеса. 2. Провести делительные и основные окружности радиусами r1, 2 и r b1,2. 3. Построить теоретическую линию зацепления как касательную к основным окружностям, проходящую через полюс зацепления Р-АВ. 4. Построить эвольвенты зубьев 1-го и 2-го колес. Построение эвольвенты 1-го колеса: - на основной окружности от точки А провести дугу ᴗ АР ʹ, равную длине отрезка АР; - разделить прямую АР и дугу ᴗ АР ʹ на четыре равные части. На прямой получаются точки Р, 1, 2, 3, 4, а на дуге – точки Р ʹ, 1 ʹ, 2 ʹ, 3 ʹ, 4 ʹ. При этом 1Р = ᴗ1 ʹ Р ʹ; 12 = ᴗ1 ʹ 2 ʹ и т.д.; - такие же отрезки деления откладываются по другую сторону от точки А. На прямой отмечаются точки 5, 6, 7, 8…, на дуге – точки 5 ʹ, 6ʹ, 7ʹ, 8ʹ…; - к радиусам О1 – 1ʹ, О1 – 2ʹ и т.д. в сторону полюса восстановить перпендикуляры, на которых отложить отрезки 1ʹ1ʹʹ = 1Р, 2ʹ2ʹʹ = 2Р и т.д. - точки Рʹ, 1ʹʹ, 2, 3ʹʹ, 4ʹʹ, 5ʹʹ, 6ʹʹ, 7ʹʹ, 8ʹʹ соединяем лекальной кривой. Построенную эвольвенту ограничиваем по высоте зуба в точке пересечения эвольвенты с окружностью вершин зубьев (ra1); - выделить практическую часть линии зацепления ab (пересечение окружностей вершин с теоретической линией зацепления). Аналогично строится эвольвента зубьев 2-го колеса. 5. Построить ножку зуба. Профиль ножки зуба колеса состоит из эвольвентной части и переходной кривой (галтели), которая соединяет эвольвентную часть с окружностью впадин. На практике пользуются упрощенным методом построения, для чего: - проводим окружности впадин для 1-го и 2-го колес соответствующими радиусами rf1 и rf2; - от точек пересечения эвольвенты с основными окружностями в направлении О1 и О2 проводим радиальные прямые; - строим сопряжение этих радиальных прямых с окружностями впадин радиусом r = 0,2 m.
Рисунок 11 – Зубчатое зацепление
6. Построить полный зуб, для чего: - по дуге делительной окружности (от точки пересечения эвольвенты с делительной окружностью) отложить толщину зуба, определяемую по формуле - провести оси симметрии зубьев и построить полные зубья (с левым и правым профилями) первого и второго зубчатых колес, используя шаблон.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.101 (0.024 с.) |
 (10)
(10)




 (14)
(14)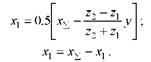
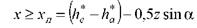


 (18)
(18)

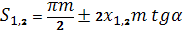 ; и толщину впадины, определяемую по формуле:
; и толщину впадины, определяемую по формуле:  ;
;


