
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение степени подвижности механизма
- Вычерчивается структурная схема механизма (без соблюдения размеров), звенья механизма нумеруются в порядкеих присоединения к стойке, начиная с кривошипа, принимаемого за входное звено. При этом стойке присваивают номер 0 (неподвижное звено), кривошипу - 1 и т. д. Таким образом, определяетсячисло подвижных звеньев – n. - Определяетсячисло кинематических пар и их класс. Кинематические пары (подвижные соединения двух звеньев) обозначаются на схеме заглавными латинскими буквами, аанализ кинематических пар сводится в таблицу 1, где указывается обозначение каждой пары; звенья, образующие пару; название пары и ее класс. В плоских механизмах встречаются только пары 5-го и 4-го классов. - Определяетсястепень подвижности механизма по формуле П.Л.Чебышева:
где n - число подвижныхзвеньев; p5 - число кинематических пар 5-гокласса; р4 - число кинематических пар 4-го класса. Таблица 1 – Анализ кинематических пар
3.1.2. Разложение механизма на структурные составляющие (группы Ассура и механизм 1 класса) Структурные группы следует отсоединять, начиная с наиболее удаленной от входного звена; при этом необходимо, чтобы после отделения очередной структурной группы механизм продолжал сохранять работоспособность, и степень подвижности оставалась бы неизменной. Отделение групп производят до тех пор, пока не останется механизм I класса, т.е. стойка, соединенная кинематической парой с входным звеном. Структурные группы изображают на чертеже отдельно, при этом нумеруют звенья и обозначают кинематические пары теми же символами, какие были использованы в структурной схеме механизма. Далее определяют класс и вид группы Ассура, обозначая класс соответствующей римской цифрой, а вид – соответствующим индексом при ней (например: II3 – группа второго класса третьего вида). Это обозначение должно быть размещено на чертеже рядом с изображением структурной группы. Отдельно на чертеже изображают механизм I класса. Проверкой правильности разложения механизма на структурные составляющие служит также их степень подвижности: у групп Ассура W = 0, у механизма I класса W = 1. После этого определяетсякласс исходного механизма (по наивысшему классу составляющих его структурных групп) и составляется егоструктурная формула [2].
3.1.3. Построение плана положений План положений механизма строится с использованием масштабного коэффициента, начиная с разметки положения неподвижных шарниров и направляющих. Подмасштабным коэффициентом понимают отношение какой-либо физической величины (в соответствующих единицах измерения) к отрезку (в миллиметрах), изображающему эту физическую величину на плане. Условимся все масштабные коэффициенты обозначать буквой μ с индексом соответствующей физической величины. Например, масштабный коэффициент плана положений определяется Фактическая длина звена (м) μ L = ---------------------------------------- (2) Длина отрезка на плане (мм) Построение плана положений необходимо начинать с положения, в котором начинается рабочий ход механизма (одно из двух крайних положений, которое в дальнейшем будем называтьнулевым. Крайнее положение определяют по траектории движения исполнительного (выходного) звена, совершающего возвратное движение: скорость его в крайних положениях равна нулю, так как меняется направление движения. В том случае, когда цикл движения механизма включает рабочий и холостой ход, положения рабочего хода определяются по заданному направлению силы полезного сопротивления, которая действует против движения выходного звена. Если направление силы полезного сопротивления не задано, то рабочий ход можно определить исходя из того условия, что по длительности, как правило, рабочий ход больше, чем холостой (иногда они равны, но не наоборот). Если механизм не имеет холостого хода, т.е. и при прямом и при обратном движениях выходного звена совершается полезная работа, то за нулевое можно принять любоеиз крайних положений. Для определенных механизмов крайнее положение определяется легко: когда кривошип составляет с кулисой прямой угол или когда кривошип и шатун располагаются на одной прямой, для других - крайние положения следует определять подбором, контролируя определением скорости выходного звена.
Построив нулевое положение механизма, строят еще как минимум пять промежуточных положений. Для этого круговую траекторию конца кривошипа делят на шесть частей (лучше равных) и нумеруют соответствующие положения в направлении вращения кривошипа. Остальные звенья в каждом из положений механизма строят последовательно засечками их длин, учитывая принятый масштабный коэффициент. Следует учесть, что план положенийдолжен включать оба крайних положения механизма, поэтому, если второе крайнее положение не вошло в число построенных шести, его строят дополнительно. Одно из положений механизма, как правило, на рабочем ходу (лучше то, для которого будет проводиться силовой анализ) выделяется основными линиями, остальные изображаются контурными. На плане положений при необходимости может быть определена траектория движения любой точки механизма, для чего последовательные положения выбранной точки соединяются плавной кривой [3]. Расчет погрешности В некоторых измерительных головках передаточный механизм содержит в себе рычажные передачи. Важной особенностью рычажных передач, используемых в измерительных средствах, является то, что контакт между сопрягаемыми элементами рычажной передачи делается скользящим. Наилучшая форма контакта — в виде сферы и плоскости, так как в этих случаях контакт теоретически осуществляется в точке, и эти поверхности относительно просто изготовить. При этом оказывается, что точность передачи зависит от того, на каком элементе передачи будет установлена плоскость, а на каком сфера и как эти плоскость и сфера расположены относительно опоры вращения. Сфера может быть установлена либо на звене, совершающем поступательное движение, либо на звене с вращательным движением (рис. 6). Для обоих этих рычагов теоретическая величина перемещений конца рычага sT при малых углах поворота равна длине рычага, умноженной на угол поворота, т. е. sT=lφ. На рис. 6(а), у рычажной передачи величина перемещения s = l*sinφ. Поэтому за механизмами, у которых сфера расположена на звене, совершающем вращательное движение, установилось название синусные передачи, а за рычагами, у которых на конце находится сфера — синусные рычаги. На рис. 6(б), у рычажной передачи сфера находится на звене, совершающем поступательное движение. Величина перемещения s = l tgφ. За такими механизмами, у которых сфера расположена на звене, совершающем поступательное движение, установилось название тангенсных механизмов, а за рычагами, у которых рабочей поверхностью является плоскость, тангенсных рычагов. Обычно в передаточных механизмах используются и синусные, и тангенсные рычаги (на рис. 6(в) рычаги 1 и 3 — синусные, а рычаг 2 – тангенсальный). Погрешность синусных рычагов. Для определения значения расчетной погрешности рычажной передачи заменим я sin ϕ формулой разложения этой тригонометрической функции в степенной ряд по углу ϕ и ограничимся членами со степенью аргумента ϕ не выше третьей:
Тогда вместо s=l Sinϕ можно написать:
Погрешность перемещения синусного рычага будет равна разности между теоретическим перемещением sT и расчетным s, т. е.
Таким образом, синусные рычаги имеют систематическую (функциональную) погрешность со знаком плюс, которая зависит от длины рычага и угла поворота. Погрешность тангенсных рычагов. Используя тот же прием, получим:
Погрешность тангенсных рычагов имеет минусовый знак и также зависит от угла поворота и длины исходного рычага. Выявленные погрешности часто называют погрешностями схемы (схемные погрешности), и они носят расчетный характер без учета погрешности изготовления. Сопоставление погрешностей синусного и тангенсного рычагов и общие рекомендации по их применению: 1. Погрешность синусных рычагов проявляется со знаком плюс (т. е. расчетные перемещения больше теоретических), а погрешности тангенсных рычагов — со знаком минус. 2. Погрешности синусного рычага в два раза меньше, чем тангенсного, при одинаковых начальных длинах рычагов и равных углах поворота. 3. При последовательной установке обоих видов рычагов можно произвести взаимную компенсацию погрешностей при соответствующей регулировке длин плеч рычагов, что и используют в рычажно-зубчатых головках. 4. Регулировкой плеч рычагов (практически это можно осуществить изменением положения сферы) можно компенсировать расчетную погрешность. 5. Зазоры в направляющих с поступательным перемещением практически не отражаются на погрешностях передачи при синусном рычаге, но проявляются значительной величиной при тангенсных рычагах (увеличивается случайная погрешность). При конструировании рычажной передачи необходимо, чтобы центр сферы располагался на прямой, проходящей через центр опоры и в исходном положении эта прямая была перпендикулярна линии перемещения поступательного звена. Если используется прямолинейный рычаг, на втором конце которого находится также сфера, то все центры сфер должны располагаться на одной линии. Если используется угловой рычаг, то центры сфер должны быть расположены в исходном положении на концах угла с вершиной на оси вращения, который должен быть дополнительным к углу между линиями измерения элементов, совершающих прямолинейное движение [4].
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 815; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.72 (0.01 с.) |
 (1)
(1)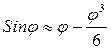 (3)
(3)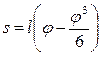 (4)
(4) (5)
(5)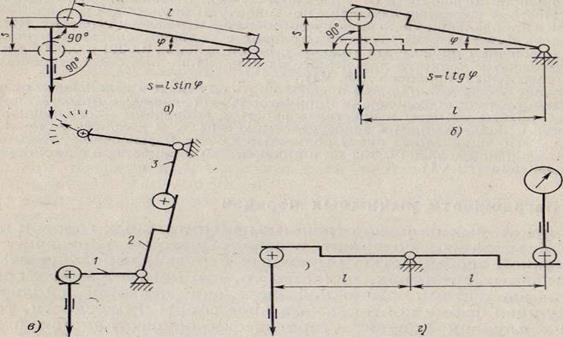 Рисунок 6 – Схемы рычажных механизмов:
а — синусного; б — тангенсного; в — двухрычажная передача с угловым рычагом; г — двухрычажная передача со сферическими опорами на одной прямой
Рисунок 6 – Схемы рычажных механизмов:
а — синусного; б — тангенсного; в — двухрычажная передача с угловым рычагом; г — двухрычажная передача со сферическими опорами на одной прямой
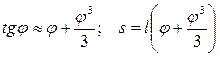 (6)
(6)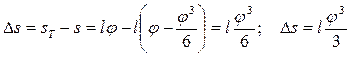 (7)
(7)


