Тема: строение вещества и спектроскопия

 

Молярная поляризация диэлектрика (определение):

Связь молярной поляризации с поляризуемостью a неполярных молекул диэлектрика (уравнение Клаузиуса-Мосотти):

Связь молярной поляризации с деформационной поляризуемостью a₀ и ориентационной поляризуемостью a_m полярных молекул (уравнение Дебая):

, a_m =

Молярная рефракция (определение)

Энергия вращения молекулы на j -том вращательном уровне:

 

E _kin = Bj (j + 1)

 

где В – вращательная постоянная.

Момент инерции двухатомной молекулы

 

I = m× ℓ ²

 

где ℓ - межъядерное расстояние, m - приведённая масса молекулы m = m ₁ m ₂/(m ₁ + m ₂), m ₁ и m ₂ – массы атомов.

Энергия гармонических колебаний двухатомной молекулы на v –ом колебательном уровне:

E_v = h n₀(v + ½)

где n₀ - частота собственных колебаний, x _e - коэффициент ангармоничности.

То же, с учетом ангармоничности колебаний:

 

E_v = h n₀(v + ½)[1 – x _e(v + ½)]

 

Молярная энергия диссоциации двухатомной молекулы:

.

 

Приложение 3. Построение графиков

 

Практика работы с графиками требует точного знания некоторых общих положений и определений математики, которые перечислены ниже в качестве напоминания.

1. Положение любой точки на плоскости может быть определено, если введена система двух координат, относительно которых положение определяется.

Наиболее распространённой является прямоугольная система координат. Такая система состоит из двух ортогональных осей, то есть двух взаимно-перпенди-кулярных прямых линий, с нанесёнными на них шкалами (см. рис. 3.1 как пример). Положение точки определяется двумя числами:

- расстоянием точки от нуля горизонтальной оси – это расстояние отсчитывается по шкале данной оси и называется абсциссой точки,

- расстоянием точки от нуля вертикальной оси – это расстояние отсчитывается по шкале соответствующей оси и называется ординатой точки.

Эти два числа образуют упорядоченную пару, обозначаемую в общем случае (х, у) и называемую координатами точки. Слово "упорядоченная пара" означает, что координаты всегда даются в последовательности (х, у) и никогда (у, х).

2. Геометрическим местом точек на плоскости называется совокупность точек, удовлетворяющих данному условию.

Данным условием обычно является некоторое алгебраическое условие. Например, геометрическим местом точек, удалённых на расстояние r от данной точки, называется окружность с центром в данной точке и с радиусом r.

3. Графиком функции у = ¦(х) называется геометрическое место точек данной функции, нанесённых на плоскость с координатными осями х и у.

Рис. 3.1. Прямоугольная система координат на плоскости

Практически график изображается непрерывной линией, называемой кривой (прямая линия рассматривается как частный случай кривой). В точном соответствии с определением графика, кривая должна быть представлена множеством точек, координаты которых удовлетворяют данному условию у = ¦(х), и которые сливаются в непрерывную линию. Например, если даны координаты центра окружности, то геометрическое место точек окружности можно изобразить с помощью циркуля.

4. Любая функция одной переменной может быть представлена графиком и, наоборот, любой график может быть представлен аналитическим выражением некоторой функции.

То есть, аналитическое выражение функции у = ¦(х) и график этой функции являются эквивалентными способами определения функции.

В связи с последним свойством, на практике встречаются два вида задач. В одном из них требуется построить график функции, которая по условию задачи дана в виде аналитического выражения у = ¦(х). В другом случае, дан график или, на самом деле, координаты ряда точек для графика, на основании которых требуется найти аналитическое выражение функции. Иными словами, в одном случае требуется найти геометрическое место точек данной функции, а в другом – найти функцию данного геометрического места точек.

В физической химии широко применяются оба вида задач.

В учебных пособиях и на аудиторной доске во время лекций обычно встречаются графики первого вида, то есть графики известной функции. Студенты могут использовать такие графики в самостоятельной работе и в ответах на теоретические вопросы. Цель этих графиков – исследовать или показать наглядно основные свойства функции. В чистой математике функции исследуются в самом общем, абстрактном виде, во всей области определения независимой переменной х. В прикладных науках аналогичные задачи отличаются некоторыми особенностями. Во-первых, обычно рассматривается поведение функции только в ограниченном интервале х, представляющем интерес в данной задаче. Во-вторых, роль переменных х и у выполняют физические величины, имеющие определённую размерность. Поэтому при построении графиков приходится решать, какие интервалы изменения х и у и какие масштабы шкал координат следует выбрать для построения графика. (Масштаб шкалы – количество единиц измерения данной физической величины, содержащееся в единице длины оси). Кроме того, единицы измерения откладываемых физических величин должны быть учтены, они должны быть указаны у каждой оси. Рассмотрим эти особенности на следующем примере.

Предположим, требуется построить график зависимости э.д.с. (E, В) электрохимической реакции в водной среде:

 

Hg₂Cl₂ (т) + H₂ (г) = 2Hg (ж) + 2H⁺ (aq) + 2Cl^– (aq)

 

от температуры J (°C):

E = 0.2676 – 3.19×10^–4(J – 25) (1)

Рис. 3.3. Правильный график функции (1)

Рис. 3.2. График функции (1), построенный без учёта физических свойств этой функции

Исходя из общих знаний о графиках, можно было бы вычислить несколько произвольных точек (х, у) и провести через них линию, как показано на рис. 3.2. (В данном случае достаточно двух точек, так как уравнение является линейным). Однако такой график является неудовлетворительным в нескольких отношениях. Во-первых, уравнение (1) фактически справедливо только в ограниченном интервале температур. Ниже приблизительно 0 °С водные растворы замерзают и эта реакция идти не может. Выше приблизительно 100 °С, при нормальном давлении, водные растворы выкипают, что так же ограничивает применимость уравнения (1). Поэтому имеет смысл строить график только для первого квадранта, при температурах от 0 до 100 °С. С другой стороны, рассматривая график как иллюстрацию изменения E с изменением J, следует позаботиться о том, чтобы наклон прямой линии был по возможности очевиден. Для этого интервал изменения E следует ограничить так, чтобы вдоль оси ординат не было слишком много "пустого пространства". Как следует из (1), при минимальной температуре 0 °С E = 0.275 В, а при максимальной 100 °С E = 0.244 В. Поэтому удобно выбрать по оси ординат интервал E от 0.24 до 0.28 В. Масштаб по оси E следует выбрать так, чтобы длины обоих осей были приблизительно одинаковыми, и весь рисунок был приблизительно "квадратным". График, построенный по этим принципам, показан на рис. 3.3.

Графики второго вида строятся аналогично. Если даны координаты точек (х, у), то сначала следует переписать их в виде таблицы, в порядке увеличения независимой переменной х. На основании этой таблицы выбрать интервалы изменения х и у и масштабы по тем же правилам, как объяснялось выше. Затем следует построить оси координат на миллиметровой бумаге и отметить точками (или другим геометрическим символом) на координатной плоскости каждую пару чисел (х, у). Точки должны быть такими, чтобы они были ясно видны на окончательном графике. Затем к этим точкам подбирают график. Если есть основания предполагать, что график должен быть линейным, то для построения графика используется линейка. Важно помнить, что заданные координаты всегда содержат некоторые погрешности. Когда мы строим график первого вида (для известной функции), у нас есть возможность вычислять координаты точек с произвольной точностью. Когда мы строим график по заданным координатам, погрешности фактически "заданы" и мы не можем их изменить. Если они сравнительно малы, то точки "ложатся на график хорошо", и построение графика не вызывает затруднений. Если погрешности велики, то график следует подбирать так, чтобы отклонение точек от него было минимальным. Например, пусть даны значения ЭДС при нескольких температурах для рассмотренной выше электрохимической реакции, которые записаны в виде таблицы:

 

J, °С
E, В	0.274	0.264	0.262	0.252	0.242

 

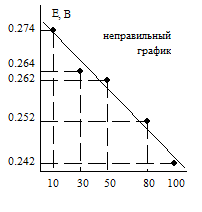
На рис. 3.4 (а) показан график, построенный по этим данным. Главный принцип этого построения состоит в следующем. Прямая линия должно быть проведена так, чтобы точки лежали либо непосредственно на ней, либо отклонялись от неё вверх и вниз (вдоль оси у) приблизительно в одинаковой степени, так чтобы все точки были удовлетворены по возможности одинаково. На рис. 3.4 (б, в г) показаны некоторые примеры неправильного построения графиков по тем же точкам.

График по заданным точкам обычно строится не просто с целью иллюстрации, а для определения неизвестных коэффициентов функциональной зависимости по найденному геометрическому месту точек. Эта задача обсуждается в следующем приложении.

 

Приложение 4. Определение коэффициентов

Функциональной зависимости

 

Многие задачи физической химии формулируются приблизительно так: Даны пары чисел (x_i, y_i), обычно в виде таблицы

 

x	x 1	x 2	……….	xN
y	y 1	y 2	……….	yN

 

Требуется определить коэффициенты уравнения y = a + bx, которое, как предполагается, лежит в основе по парного соответствия чисел x_i и y_i.

Если бы число пар чисел (x_i, y_i) было равно двум, то коэффициенты находились бы решением системы уравнений

y ₁ = a + bx ₁

y ₂ = a + bx ₂

 

Как известно, решением такой системы относительно a и b является:

; или a = y ₁ – bx ₁ или a = y ₂ – bx ₂ (1)

Однако в большинстве задач число данных пар (x_i, y_i) превышает 2. Если бы данные числа были точными, то можно было бы выбрать любые две пары (x_i, y_i), составить из них систему уравнений и решить её относительно a и b. Такое решение было бы общим и единственным для всей таблицы. В реальных задачах, однако, числа (x_i, y_i) содержат погрешности измерений или округлений. С точки зрения чистой математики, в этом случае система уравнений не совместима и не имеет единственного решения. В прикладных науках проблема ставится несколько иначе: требуется найти такие коэффициенты a и b, которые удовлетворяют данным парам чисел (x_i, y_i), в некотором смысле, наилучшим образом. Для нахождения такого решения есть несколько методов. Ниже рассматриваются два из них, наиболее распространённые в исследовательской и инженерной практике.

 

(б)

(а)

Рис. 3.4 (а) График зависимости ЭДС от температуры, построенный по экспериментальным данным (черные точки) (б, в, г) Примеры неправильного построения графиков по одним и тем же экспериментальным точкам. (Другой пример неправильного графика см. на рис. 3.2)

 

Графический метод заключается в том, что на координатную плоскость наносят точки (x_i, y_i) и подбирают к ним график (прямую линию) так, чтобы отклонение точек от него было по возможности минимальным. Выбирают затем любые две точки, принадлежащие графику, определяют их координаты (x ₁, y ₁) и (x ₂, y ₂) и вычисляют a и b по уравнениям (1). Полученный коэффициент b называют угловым коэффициентом или коэффициентом наклона, а а – начальной ординатой графика или свободным членом линейного уравнения. Иногда процедуру определения b называют нахождением тангенса угла наклона, однако это нельзя понимать буквально, как определение угла наклона транспортиром в градусах и вычисление тангенса, потому что реальный угол наклона графика на рисунке зависит от выбранных масштабов шкал осей координат.

Чтобы лучше понять этот метод, выполните следующее упражнение.

Упражнение. Посмотрите на рис. 4.1 и внимательно прочтите подпись к нему.

1) Убедитесь, что уравнения 1 правильные. Для этого вычислите для графика А по координатам точек 1 (9, 14) и 2 (0, 10) коэффициенты:

= ; a = y ₁ – bx ₁ = 14 – b× 9 =

Так как прямая А представляет график уравнения у = 10 + 0.444 х, должно получиться b = 0.444 и а = 10.0.

Рис. 4.1 (для упражнения) Графики линейных функций. А: График функции у = 10 + 0.444 х, построенный по двум точкам 1 и 2 с координатами (9, 14) и (0, 10) соответственно, В: График функции у = 8 – 0.322 х, построенный по двум точкам 3 и 4, С: График неизвестной функции, построенный по экспериментальным точкам (черные точки).

2) С помощью сетки на рис. 4.1 определите координаты точек 3 и 4 графика В. Постарайтесь сделать это с точностью до десятой доли цены деления шкалы каждой оси. Вычислите:

и a = y ₄ – bx ₄ или и a = y ₃ – bx ₃

Если координаты определены правильно, то должно получиться b = –0.32 и а = 8.0, соответственно уравнению у = 8 – 0.322 х графика В.

3) Выберите любые две точки (их можно обозначить 5 и 6), принадлежащие графику С, и определите их координаты. (Обратите внимание, что черные точки, по которым построен график С, не принадлежат ему). Вычислите:

и a = y ₆ – bx ₆

Тем самым определены коэффициенты линейной функции, заданной графиком. (Правильный результат определения b = 0.32 и а = 9.0)

 

Более точные значения a и b можно получить вычислительным методом наименьших квадратов (общепринятое сокращение МНК). Согласно этому методу, a и b должны быть такими, чтобы сумма квадратов отклонений

была минимальной. Из этого условия следует:

, (2)

где N – число пар (x_i, y_i). Имея таблицу данных (x_i, y_i), a и b можно найти по уравнениям (2) без помощи графика. Тем не менее, график в этом случае обычно строят, чтобы убедиться, что все точки достаточно хорошо "ложатся" на прямую линию.

Эти два метода применимы непосредственно только к линейным зависимостям. К сожалению, большинство теоретических уравнений физической химии являются нелинейными и могут содержать, в зависимости от конкретной задачи, один или более неизвестных коэффициентов, которые требуется определить.

Если теоретическое уравнение, лежащее в основе данных пар чисел (X_i, Y_i), является нелинейным вида Y = ¦(Х, A, B), то описанные выше методы можно применить после преобразования этого уравнения в линейное уравнение с новыми переменными y = a + bx, в котором х и у – функции Х и Y и любых известных параметров, но не искомых А и В, а a и b – функции искомых А и В и любых известных параметров, но не переменных Х и Y. Эта процедура называется линеаризацией функции. Вычислив новые переменные (x_i, y_i), их обрабатывают графическим или вычислительным методом, как описано выше, и из полученных коэффициентов a и b находят искомые А и В.

В качестве примера рассмотрим следующую задачу. Найти число обращения фермента k и константу Михаэлиса К _М в уравнении Михаэлиса-Ментена:

(3)

по следующим данным о зависимости начальной скорости v некоторой ферментативной реакции от начальной концентрации субстрата [S] при концентрации энзима [E]_o 1.00×10^–5 ммоль/л.

 

[S], ммоль/л	2.00	1.25	1.00	0.50	0.25
v ×10^3, ммоль/(л·с)	0.49	0.47	0.46	0.35	0.27

 

Так как уравнение (3) является нелинейным (гиперболическая функция), его следует преобразовать в линейное с новыми переменными, и применить методы определения коэффициентов, описанные выше. Возможны, например, следующие способы линеаризации.

1) Возьмем обратную величину от обоих частей уравнения (3):

(4-1)

Это уравнение имеет вид у = а + bx с у = v ^–1, x = [S]^–1, a = (k [E]_o)^–1, b = K _M(k [E]_o)^–1 = K _M a.

2) Умножим обе части уравнения (4-1) на [S].

(4-2)

Это уравнение имеет вид у = а + bx с у = [S]/ v, x = [S], b = (k [E]_o)^–1, а = K _M(k [E]_o)^–1 = K _M b.

3) Умножим обе части уравнения (3) на знаменатель правой части:

 

vK _M + v [S] = k [E]_o[S]

 

Поделив обе части на [S], получим:

v = k [E]_o – K _M v [S]^–1 (4-3)

 

В этом линейном уравнении у = v, х = v [S]^–1, a = k [E]_o, b = – K _M.

Можно использовать любое из этих преобразований, чтобы найти коэффициенты а и b графическим методом или методом МНК и затем вычислить из них искомые k и К _М.

Рассмотрим подробно способ (4-1) с у = v ^–1, x = [S]^–1, a = (k [E]_o)^–1, b = K _M a. Перепишем данные величины [S] и v ×10³ в отдельной таблице (столбцы 1 и 2 в табл. 4.1) и вычислим в ней обратные величины [S]^–1 и (v ×10³)^–1 (столбцы 3 и 4). Построим график зависимости (×10³)^–1 от [S]^–1. Как видно (рис. 4.2), график получается действительно линейным. Выберем на нём две точки произвольно, но с тем ограничением, чтобы они лежали не слишком близко друг к другу. (Если выбрать близко лежащие точки, то точность определения коэффициентов а и b может быть низкой). Например, это могут быть точки 1 и 2 (рис. 4.3) с абсциссами = 0.25 л/ммоль и = 3.8 л/ммоль. Определим их ординаты из графика: = 1.88 л·с/ммоль и = 3.64 л·с/ммоль. Однако для вычисления а и b нужны координаты ([S]₁^–1, v ₁^–1) и ([S]₂^–1, v ₂^–1), а не их десятичные производные. Поэтому преобразуем полученные ординаты:

= = 1.88 л·с/ммоль; = 1.88×10³ л·с/ммоль;

= = 3.64 л·с/ммоль; = 3.64×10³ л·с/ммоль;

Подставим теперь ([S]₁^–1, v ₁^–1) и ([S]₂^–1, v ₂^–1) в уравнения (1). Для углового коэффициента получим:

= 500 с.

Для свободного члена а:

a = = 1.88×10³ – 500×0.25 = 1.76×10³ л·с/ммоль.

 

 

Таблица 4.1

 

[S], ммоль/л	v ×10^3, моль/(л·с)	[S]^–1, л/ммоль	(v ×10^3)^–1, л·с/ммоль	xy ×10^–3 с·(л/ммоль)^2	x ^2 (л/ммоль)^2
2.00	0.49	0.500	2.04	1.02	0.25
1.25	0.47	0.800	2.13	1.70	0.64
1.00	0.46	1.00	2.17	2.17	1.00
0.50	0.35	2.00	2.86	5.72	4.00
0.25	0.27	4.00	3.70	14.80	16.00
		S х =8.30	S у ×10^–3 =12.90	S xy ×10^–3 = 25.41	S х ^2 = 21.89
			S у =12.90×10^3	S xy = 25.41×10^3

 

Рис. 4.2 График зависимости обратной величины скорости ферментативной реакции от обратной величины концентрации субстрата.

Так как a = (k [E]_o)^–1, то k = (a [E]_o)^–1 = (1.76×10³×1.00×10^–5)^–1 = 57 с^–1. Так как b = K _M a, то K _M = b / a = 500/1.76×10³ = 0.28 ммоль/л. Таким образом, k = 57 с^–1, K _M = 2.8×10^–4 моль/л.

Рис. 4.3 Определение коэффициентов а и b.

Рассмотрим решение этой же задачи методом наименьших квадратов. Заметим, что точки на графике (рис. 4.2) ложатся удовлетворительно на прямую линию, поэтому мы вправе применить метод МНК. Для удобства вычислений по уравнениям (2) введём обозначения х = [S]^–1, у = v ^–1. Заметим, что в столбце 4 находятся величины (v ×10³)^–1 = v ^–1×10^–3 = у ×10^–3. Вычислим суммы S х и S у ×10^–3 по столбцам 3 и 4 в таблице и запишем их внизу таблицы. Вычислим в столбцах 5 и 6 произведения xy ×10^–3 и квадраты х ² и так же найдем суммы. В уравнения (2) входят суммы S у и S xy, а не S у ×10^–3 и S ху ×10^–3. Поэтому в последней строке таблицы преобразуем эти суммы. Так как число пар (x_i, y_i) равно 5 (N = 5), то по уравнениям (2) получается для углового коэффициента:

= = 493 с

для свободного члена:

= = 1.76×10³ с·л/ммоль

Очевидно, эти результаты практически совпадают с теми, что были получены графическим методом, однако они, в принципе, более точные, так как построение графика "по точкам" даёт надёжные результаты только тогда, когда точки "хорошо ложатся" на прямую линию.

 

Приложение 5. Примеры решения задач

 

Пример 1 (тема: второй закон термодинамики) Вычислить энтропию обратимого процесса, в начальном состоянии которого 2 моля идеального газа находятся при 20 °С и давлении 1.00 атм, а в конечном состоянии то же количество газа находится при 50 °С и давлении 7.75 атм. Молярная изобарная теплоёмкость газа 5 R /2.

Решение. По условию задачи, идеальный газ претерпевает изменение температуры и давления в обратимом процессе. Поэтому первой целью является нахождение зависимости энтропии от температуры и давления.

По второму закону термодинамики, изменение энтропии в обратимом процессе составляет d S = d Q / T. По первому закону d Q = d U + p d V, если механическая работа против внешнего давления является единственным видом работы, совершаемой системой. Отсюда следует общее уравнение:

T d S = d U + p d V (1)

С другой стороны, в условии задачи дана изобарная теплоёмкость, которая связана с внутренней энергией U через энтальпию H:

 

C_P = d H /d T; C_P d T = d H = d(U + pV) = d U + p d V + V d p

 

Выразим отсюда d U: d U = C_P d T – p d V – V d p

и подставим в (1): T d S = C_P d T – p d V – V d p + p d V = C_P d T – V d p

 

Таким образом, получено уравнение, выражающее энтропию обратимого процесса как функцию T и p:

В первом слагаемом, коэффициент С_Р = 5 R /2 не зависит от температуры, поэтому его можно интегрировать в том виде, как он есть. Коэффициент второго слагаемого, – V / T, является функцией давления. Для одного моля идеального газа можно записать pV = RT, откуда следует V / T = R / p. Таким образом, получается зависимость энтропии от температуры и давления в явном виде, пригодном для решения задачи:

Изменение энтропии можно найти интегрированием этого выражения в пределах температуры и давления, указанных в задаче (от Т ₁ = 273 + 20 = 293 K и р ₁ = 1.00 атм, до T ₂ = 273 + 50 = 323 К и р ₂ = 7.75 атм). Из приложения 4 узнаем, что первообразная от функции 1/ х равна ln(x). Поэтому:

= =

Подставив соответствующие значения температуры и давления, получим

D S = = –15.0

с единицами измерения, отвечающими газовой постоянной R, Дж/(моль К), так как логарифмические члены являются безразмерными. Таким образом, изменение энтропии составляет –15.0 Дж/К на 1 моль газа. (Фактически, получилось изменение молярной энтропии). В условии задачи требуется найти изменение для 2 молей газа, поэтому в окончательном ответе получим D S = 2×(–15.0) = –30.0 Дж/К.

Заметим, что для вычисления дроби р ₂/ р ₁ можно использовать любые единицы измерения давления, так как дробь безразмерна и все единицы измерения давления пропорциональны друг другу. Поэтому в этом случае нет необходимости переводить атмосферы в единицы СИ, паскали. Однако, для вычисления дроби Т ₂/ Т ₁ градусы Цельсия необходимо перевести в единицы СИ, потому что практическая шкала Цельсия и шкала термодинамической температуры сдвинуты относительно друг друга на 273.15 К. То есть, температуры в этих шкалах не пропорциональны. Фактически, температуру Цельсия и термодинамическую температуру следует рассматривать как разные физические величины, что подчеркивается их обозначениями, J и Т.

 

Ответ: D S = –30.0 Дж/К

 

Пример 2 (тема: химические равновесия) Газообразные вещества А, В и Z реагируют по уравнению 1/2А + В = 3Z при повышенной температуре. Когда в реактор вводят 1/2 моля А и 1 моль В и смесь нагревают до равновесия при 500 К, равновесное количество А оказывается равным 0.450 моль, а суммарное равновесное давление партнеров реакции 50.3 кПа. Вычислите константы равновесия К_Р и К_С, а так же стандартную энергию Гиббса реакции при этой температуре.

Решение. По определению, константами равновесия К_Р и К_С реакции 1/2А + В = 3Z называются величины:

и (1)

где р _А, р _В и р _Z – равновесные парциальные давления А, В и Z, С _А, С _В и С _Z – равновесные молярные концентрации А, В и Z.

Сосредоточимся сначала на константе К_Р. По закону Дальтона общее давление газовой смеси равно сумме парциальных давлений компонент:

р = р _А + р _В + р _Z

причем парциальное давление любого компонента может быть найдено из общего давления, если известна мольная доля компонента в смеси:

р _А = х _А р, р _В = х _В р, р _Z = х _Z р

(мольная доля х – отношение числа молей данного компонента к числу молей всех компонент). Если парциальные давления в формуле для К_Р выразить через общее давление, то получится

(2)

Таким образом, начинать решение следует с вычисления равновесных чисел молей компонент.

Чтобы сделать пример решения более общим, запишем уравнение реакции в виде:

а А + b B = z Z (3)

 

(где а, b, z – стехиометрические коэффициенты) и введём обозначения: n – общее число молей при равновесии, n _A0, n _B0, n _Z0 – начальные числа молей компонент, которые были введены в реактор, n _A, n _B, n _Z – равновесные числа молей компонент. Условие задачи в этих обозначениях выглядит, как показано в рамке справа.

Для вычисления мольных долей компонент, необходимо найти равновесные числа молей n _B и n _Z (n _A известно из условия). Чтобы найти их, воспользуемся свойством стехиометрического уравнения, по которому изменения чисел молей D n_i реагирующих веществ не независимы, а связаны между собой через химическую переменную x:

, (4)

, (5)

где n_i – конечные (равновесные) ячисла молей участников реакции, n_{i ,0} – их числа молей, n _i – стехиометрические коэффициенты со знаком плюс у продуктов и со знаком минус у исходных веществ. Так как известны все начальные числа молей и известно равновесное число молей А, то можно вычислить x по данным для А:

С помощью (5) вычисляем затем:

n _В = n _В,0 – b x = 1 – 1×0.100 = 0.900 моль,

n _Z = n _Z,0 + z x = 0 + 3×0.100 = 0.300 моль.

Общее число молей в смеси при равновесии составляет n = n _A + n _B + n _Z = 0.450 + 0.900 + 0.300 =1.650 моль. Поэтому

 

x _A = 0.450/1.650 = 0.273, x _B = 0.900/1.650 = 0.545, x _Z = 0.300/1.650 = 0.182.

 

Подставив эти значения в уравнение (2), получим

2.38×10⁵ Па^3/2

Для вычисления К _С необходимо знать, как давление газа связано с его концентрацией. Так как в условии задачи об этом не сказано ничего, предположим, что компоненты смеси имеют свойства идеального газа. Для идеального газа pV = nRT, откуда следует n / V = p / RT и C = p / RT, так как n / V (число молей /объём) = С (молярная концентрация), то есть С _А = p _А/ RT, С _В = p _В/ RT, С _Z = p _Z/ RT. Подставляя эти выражения в определяющее уравнение для К _C (уравнение 1), получим:

= = =

2.38×10⁵×(8.315×500)^–3/2 = 0.888

с единицами измерения:

= = =

(смотри приложение 1 для перевода единиц измерения).

Таким образом, К_Р = 2.38×10⁵ Па^3/2, К_С = 0.888 (моль/м³)^3/2.

Стандартную энергию Гиббса реакции необходимо вычислять по уравнению D G ° = – RT ln K°, где К° – термодинамическая константа равновесия (безразмерная величина), связанная с активностями компонент. Так как наша газовая смесь предполагается идеальной, коэффициенты активностей равны 1 и константа К° равна численному значению (то есть, значению без единиц измерения) константы К_Р или К_С. Однако численные значения термодинамических функций зависят от стандартного состояния, от которого отсчитываются их изменение. Если возьмем численное значение К_Р = 2.38×10⁵ в качестве К°, то получим величину D G ° = –51.5 кДж/моль, которая относится к стандартному состоянию газа с давлением 1 Па. Эта величина D G ° имеет смысл изменения энергии Гиббса в обратимом процессе, ведущем от начального состояния, в котором p _A = 1 Па, p _B = 1 Па, p _Z = 0 Па, к конечному состоянию с p _A = 0 Па, p _B = 0 Па, p _Z = 1 Па. Если возьмем численное значение К_С = 0.888, то получим величину D G ° = 0.494 кДж/моль. Эта величина относится к обратимому процессу, ведущему от начального состояния с концентрациями C _A = 1 моль/м³, C _B = 1 моль/м³, C _Z = 0 моль/м³, к конечному состоянию с концентрациями C _A = 0 моль/м³, C _B = 0 моль/м³, C _Z = 1 моль/м³.

Стандартные состояния являются предметом профессиональных конвенций (договорённостей между химиками). Общепринятым (то есть, конвенционным) стандартным состоянием газообразных веществ является такое, в котором газ имеет идеальные свойства и давление р ° = 1 атм* (р ° – парциальное давление в смеси или общее давление в однокомпонентной системе). Поэтому, для правильного решения, К_Р или К_С следует перевести в атмосферы, и численное значение использовать в качестве К°. Из приложения 1 можно узнать, что 1 атм = 1.01325×10⁵ Па, откуда следует 1 Па = (1.01325×10⁵)^–1 атм = 9.869×10^–6 атм. Таким образом:

 

К_Р = 2.38×10⁵ Па^3/2 = 2.38×10⁵×(9.869×10^–6 атм)^3/2 = 2.38×10⁵×(9.869×10^–6) ^3/2 (атм)^3/2

 

= 2.38×10⁵×3.100 ×10^–8 атм^3/2 = 7.379×10^–3 атм^3/2

 

К° = 7.379×10^–3

 

D G ° = – RT ln K° = – 8.315×500×ln(7.379×10^–3) = 2.04×10⁴