Устойчивость систем управления. Теорема Ляпунова для линейных систем.

Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения.

Возмущения

отрицательные или «ветровые»

положительные или «полезные»

Устойчивая САУ — система в которой переходные процессы являются затухающими.

(a ₀ pⁿ + a ₁ p^{n − 1} +... + a_n) y = (b ₀ p^m + b ₁ p^{m − 1} +... + b_m) g — операторная форма записи линеаризированного уравнения.

y(t) = y _уст (t)+y _п = y _вын (t)+y _св

y _уст (y _вын) частное решение линеаризированного уравнения

y _п (y _св)общее решение линеаризированного уравнения, как однородного дифференциального уравнения, то есть D (p) = (a ₀ pⁿ + a ₁ p^{n − 1} +... + a_n) y = 0

САУ устойчива, если переходные процессы у_n(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть при

Решая дифференциальное уравнение в общем случае, получим комплексные корни p_i, p_i+1 = ±α_i ± jβ_i

Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:

, где ,

Из полученных результатов видно, что:

при ∀α_i<0 выполняется условие устойчивости, т.е. переходный процесс с течением времени стремиться к у_уст (Теорема Ляпунова 1);

при ∃α_i>0, выполняется условие неустойчивости (Теорема Ляпунова 2), то есть , что приводит расходящимся колебаниям;

при ∃α_i=0 и ∃α_i>0 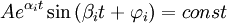, что приводит к незатухающим синусоидальным колебаниям системы(система на границе устойчивости) (Теорема Ляпунова 3)

Теорема Ляпунова

Часто приходится иметь дело с такими случайными величинами, которые являются суммами большого числа независимых случайных величин. При некоторых весьма общих условиях оказывается, что эта сумма имеет распределение, близкое к нормальному, хотя каждое из слагаемых может не подчиняться нормальному закону распределения вероятностей. Эти условия были найдены Ляпуновым и составляют содержание теоремы, названной его именем. Приведём без доказательства только следствие из теоремы Ляпунова.

Пусть с ξ₁,ξ₂,...,ξ _n,… последовательность попарно независимых случайных величин с математическими ожиданиями M(ξ _i) = α _i и дисперсиями D 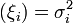, причём эти величины обладают следующими двумя свойствами:

1) Cуществует такое число L, что для любого i имеет место неравенство , т, е. все значения случайных величин, как говорят, равномерно ограничены, относительно математических ожиданий;

2) Сумма неограниченно растёт при

Тогда при достаточно большом n сумма ξ = ξ₁ + ξ₂ +... + ξ _n имеет распределение, близкое к нормальному.

Пусть α и σ математическое ожидание и дисперсия случайной величины ξ = ξ₁ + ξ₂ +... + ξ _n. Тогда
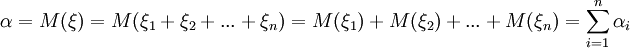