Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы циклической структурыСодержание книги
Поиск на нашем сайте
Часто при решении задач приходится многократно вычислять значение по одним и тем же алгоритмам. Такие многократно повторяемые алгоритмы называются циклами. Различают циклы с заданным и неизвестным числом повторений. К последним относятся итерационные циклы, характеризующиеся последовательным приближением к искомому значению с заданной точностью. Для организации цикла необходимо выполнить следующие действия: 1) задать перед циклом начальное значение переменной, изменяющейся в цикле; 2) изменять переменную перед каждым новым повторением цикла; 3) проверять условие окончания или повторения цикла; 4) управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из него по окончании. Последние три функции выполняются многократно. Переменная, изменяющаяся в цикле, называется параметром цикла. 1. Вычислить значения функции 2. Вычислить и вывести на печать положительные значения функции у=sin (nx) ‑ cos (n/x) при n = 1, 2, …, 50. 3. Вычислить значения функции z = xk/k, большие а, если k=1, 2, …. 4. Вычислить значения функции у = а3/(а2 + х2) при х, изменяющемся от 0 до 3 с шагом 0,1. 5. Напечатать таблицу значений аргумента х и функции у(х) = а3/(а2 + х2) при значении х, изменяющихся от 0 до 3 с шагом 0,1. 6. Составить программу для вычисления значения функции у = 7. Составить программу вычисления n! (1 . 2 . 3 . 4.... . n): 8. Составить программу, вычисляющую экстремальное значение функции 9. Вычислить: а) у = (2n ‑1)! = б) у = (2n)! = в) у = n!, n > 0. 10. Вычислить: у = 11. Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3). 12. Дано целое n >2. Напечатать простые числа из диапазона [2, n]. 13. Найти сумму цифр заданного натурального числа. 14. Вычислить k ‑ количество точек с целочисленными координатами, попадающих в круг радиуса R (R>0) с центром в начале координат. 15. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр. 16. Даны целое n и вещественные числа 17. Напечатать все простые делители натурального числа. 18. Уравнение (предложена М.В. Дякиным). Дана последовательность Написать программу, которая для заданного натурального где Программа должна найти и сообщить: 1) точное значение x в виде несократимой дроби; 2) сумму цифр числителя и сумму цифр знаменателя этой дроби. Образец вывода результата: Число 6, числитель дроби X=10, знаменатель дроби X=63. Сумма цифр числителя =1, сумма цифр знаменателя =9. 19. Задача « Кучи и яма»(предложена А.Б. Дернятиным). Имеются яма и несколько куч (не более пяти) кирпичей. Разрешается перекладывать кирпичи из куч в яму по следующему правилу: если количество кирпичей в куче больше, чем в яме, то можно переложить столько кирпичей, сколько находится в яме в данный момент. Требуется разработать алгоритм, который позволяет уложить в яму как можно больше кирпичей. Образец вывода результатов: К1=150001 К2=81234 Я=70000 было К1=150001 К2=11234 Я=140000 в яму из кучи 2‑й К1=10001 К2=11234 Я=280000 в яму из кучи 1‑й 20. Представления натурального числа (предложена Д.Я.Шараевым). Известно, что любое натуральное число N (0<N Пример. N=4. S=2. (12+12+12+12=4, 22=4) 21. Задача «Многоугольник»(предложена Н.Ю. Лукояновым). На плоскости декартовыми координатами своих вершин дан выпуклый Входные данные: Выходные величины: координаты (ха, ya) и (xb, yb) точек пересечения лучей a и b с границей
Алгоритмы работы с рядами При работе с рядами обычно составляют рекуррентную формулу, которая задает значение i+1-го члена ряда (Y(i+1)) через значения предыдущих членов, чаще ‑ i-го члена ряда (Y(i)). Обычно используют отношение i+1-го члена к i-му члену, подставляют их значения, и после преобразований получается рекуррентная формула. Пример. Вычислить значение членов бесконечного ряда 1. Вычислить сумму членов для следующих рядов с точностью до 10-4: а) б) Для вычисления текущего значения члена ряда использовать рекуррентную формулу в) г) д) е) ж) Текущий член ряда вычислять, используя рекуррентную формулу. 2. Составить программу вычисления значений членов убывающей последовательности 3. Составить программу вычисления членов бесконечного ряда z = с точностью до10-4. 4. Не используя стандартные функции (за исключением abs), вычислить с точностью до 10-4: а) б) в) г) 5. Вычисление f = 10! 6. Вычислить: а) у = cos(x)+ cos(x2) + cos(x3) +…+cos(x30); б) у = 1! + 2! + 3! + …+ n! (n>1);
в) у ‑ первое из чисел sin(x), sin(sin(x)), sin(sin(sin(x,…))), меньшее по модулю 10-4. 7. Числа Фибоначчи («fn») определяются по формулами f0 = f1 = 1; fn = fn-1 + fn-2 при n = 2, 3, …: а) определить четвертое число Фибоначчи; б) вычислить первое число Фибоначчи, большее m (m > 1); в) вычислить s ‑ сумму всех чисел Фибоначчи, которые не превосходят 1000.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.104.132 (0.006 с.) |

 , если Х задано массивом, состоящим из 40 элементов.
, если Х задано массивом, состоящим из 40 элементов.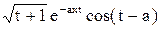 при одновременном изменении аргументов t от 2 до 3 с шагом 0,2 и х от 1 до 2 для а = ‑2,1.
при одновременном изменении аргументов t от 2 до 3 с шагом 0,2 и х от 1 до 2 для а = ‑2,1. при изменении аргумента х от 0 до 4 с шагом h.
при изменении аргумента х от 0 до 4 с шагом h. …
…  , n >0;
, n >0; …
…  , n >0;
, n >0;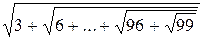 .
. Рассматривая пары
Рассматривая пары 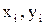 как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.
как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки. ,
,  ‑ натуральное число. Квадратные скобки
‑ натуральное число. Квадратные скобки  обозначают в формуле взятие целой части (округление до ближайшего меньшего целого числа). Обозначим
обозначают в формуле взятие целой части (округление до ближайшего меньшего целого числа). Обозначим  .
.
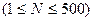 решает уравнение
решает уравнение  ,
, - обозначение числа
- обозначение числа 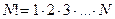 .
.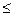 1000) может быть представлено в виде суммы квадратов не более четырех положительных целых чисел. Составьте программу, которая в ответ на ввод числа N выводит количество S всех различных представлений этого числа. Представления, отличающиеся лишь порядком слагаемых, считаются одинаковыми.
1000) может быть представлено в виде суммы квадратов не более четырех положительных целых чисел. Составьте программу, которая в ответ на ввод числа N выводит количество S всех различных представлений этого числа. Представления, отличающиеся лишь порядком слагаемых, считаются одинаковыми. -угольник. Его вершины пронумерованы от 1 до n в порядке следования против часовой стрелки. Задан номер
-угольник. Его вершины пронумерованы от 1 до n в порядке следования против часовой стрелки. Задан номер 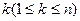 . Требуется провести через
. Требуется провести через  -вершину
-вершину  точностью до члена
точностью до члена 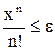 . Считать, что требуемая точность (ε) достигнута, если очередное слагаемое по модулю меньше указанной точности и все последующие слагаемые можно уже не учитывать. Определим рекуррентную формулу Y(i+1)/Y(i)=(x(i+1)/(i+1)!)/(xi/i!)=x/i. Получим рекуррентную формулу Y(i+1)=Y(i)*x/(i+1).
. Считать, что требуемая точность (ε) достигнута, если очередное слагаемое по модулю меньше указанной точности и все последующие слагаемые можно уже не учитывать. Определим рекуррентную формулу Y(i+1)/Y(i)=(x(i+1)/(i+1)!)/(xi/i!)=x/i. Получим рекуррентную формулу Y(i+1)=Y(i)*x/(i+1).

 , где n ‑ номер члена ряда. Начальное значение у принять равным
, где n ‑ номер члена ряда. Начальное значение у принять равным  ;
; ;
;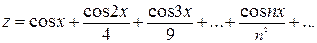 ;
;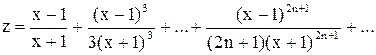 ;.
;. ;
; .
. … с точностью до10-4.
… с точностью до10-4.