
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика организации и оцениванияСодержание книги
Поиск на нашем сайте
Проведение тестирования возможно как на бумажных носителях, так и на компьютере. На тестирование отводится 45 минут. Тестируемый должен выбрать правильный ответ и записать его в листе ответа, если тестирование организуется на бумажных носителях, или выделить значком на мониторе компьютора. Если правильных ответов более одного это специально оговаривается в условии задачи. В случае если хотябы один из правильных ответов, предполагаемых в задачи не указан, задача считается не выполненной. За каждое правильно выполненное задание тестируемому дается один балл. Критерии оценки: 20 – 24 баллов – «удовлетворительно»; 25 – 29 балла – «хорошо»; 30 – 35 баллов – «отлично». Менее 20 баллов – «неудовлетворительно».
СОДЕРЖАНИЕ ТЕСТА
1. Декартова прямоугольная система координат на плоскости задается: А: двумя прямыми и единичными отрезками на каждой прямой; В: двумя прямыми, единичным отрезком и положительным направлением на одной из прямых; С: двумя перпендикулярными прямыми, единичным отрезком и положительным направлением на каждой из прямых; D: двумя пересекающимися прямыми и положительным направлением на каждой из прямых. 2. А: точка А имеет координаты (3; 4); В: точка А имеет координаты (5; 3); С: точка А имеет координаты (2; 4); D: точка А имеет координаты (-3; 5). . Рис1 3. По формуле А: расстояние между двумя точками плоскости; В: расстояние отточки до прямой; С: угол между двумя прямыми; D: длина отрезка. 4. Формулы А: расстояние от точки до прямой; В: координаты точки, которая делит данный отрезок в данном отношении; С: расстояние между двумя точками; D:угол между двумя прямыми. 5. Координаты середины отрезка находятся как А: полусумма соответствующих координат его концов; В: полуразность соответствующих координат его концов; С: полусумма квадратов соответствующих координат его концов; D: сумма квадратов соответствующих координат его концов. 6. Формула А: абсциссу точки пересечения биссектрис произвольного треугольника; В: ординату точки пересечения серединных перпендикуляров к сторонам произвольного треугольника; С: абсциссу точки пересечения медиан треугольника; D: ординату точки пересечения высот произвольного треугольника. 7. Формула А: площадь треугольника с вершинами в точках А (х 1; у 1), В (х 2; у 2), С (х 3; у 3); В: координаты точки пересечения медиан треугольника; С: точку пересечения трех прямых; D: периметр треугольника с вершинами в точках А (х 1; у 1), В (х 2; у 2), С (х 3; у 3). 8. Полярная система координат на плоскости задается: А: двумя пересекающимися прямыми, углом, между этими прямыми и единичным отрезком; В: точкой, произвольным лучом, выходящим из этой точки и единичным отрезком; С: двумя пересекающимися прямыми, единичным отрезком и положительным направлением на каждой из прямых; D: произвольной прямой и углом, принятым за единицу измерения углов. 9. Полярными координатами произвольной точки плоскости являются А: абсцисса и ордината; В: полюс и полярная ось; С: угол и проекция точки на полярную ось D: полярный радиус и полярный угол 10. Общее уравнение прямой имеет вид А: Ах + Ву + С = 0 В: Ах + Вху + Сх = 0 С: у = ах + в D: Ах + Ву + С 11. При В = 0 общее уравнение прямой задает прямую А: проходящую через начало координат; В: параллельную оси ординат; С: параллельную оси абсцисс; D: не является уравнением прямой. 12. Данное уравнение А: уравнением эллипса; В: общим уравнением прямой; С: нормальным уравнением прямой; D: уравнение прямой в отрезках. 13. Уравнение прямой вида у = ах + в называется (должно быть выбрано не менее двух вариантов ответа) А: уравнением прямой с угловым коэффициентом; В: уравнением прямой, разрешенным относительно ординаты; С: нормальным уравнением прямой; D: общим уравнением прямой. 14. По формуле А: полярный угол нормали; В: угловой коэффициент произвольной прямой; С: угол между прямыми; D: угол между прямой и плоскостью. 15. Уравнение прямой вида А: уравнением прямой в орезках; В: общим уравнением прямой; С: нормальным уравнением прямой; D: уравнением прямой, проходящей через две данные точки. 16. Условием параллельности двух прямых является (должно быть выбрано не менее двух ответов) А: равенство начальных ординат; В: равенство угловых коэффициентов; С: пропорциональность коэффициентов при соответствующих переменных; D: выполнение условия а > в 17. Две прямые перпендикулярны, если (должно быть выбрано не менее двух ответов) А: их угловые коэффициенты противоположны по знаку и обратны по абсолютной величине; В: если для коэффициентов при переменных х и у в общих уравнениях прямых выполняется равенство А1В2=-А2В1; С: если равны их начальные ординаты; D: если для коэффициентов при переменных х и у в общих уравнениях прямых выполняется равенство А1А2=-В1В2. 18. Порядок кривой равен А: высшей степени переменной у, входящей в данное уравнение; В: коэффициенту при переменной у; С: коэффициенту при произведении ху; D: высшей степени переменных х и у, входящих в данное уравнение. 19. Уравнение кривой второго порядка обязательно содержит А: один из коэффициентов при переменных х или у равный 2; В: квадрат хотя бы одной из переменных х или у, или произведение ху; С: слагаемое содержащее произведение ху; D: произвольное постоянное число. 20. Окружностью называется А: множество точек пространства удаленных от данной точки на данное расстояние; В: множество точек плоскости удаленных от данной точки, называемой центром окружности, на данное расстояние, называемое радиусом окружности; С: геометрическое место точек равноудаленных от двух фиксированных прямых; D: множество точек плоскости удаленных от данной прямой на данное расстояние. 21. Уравнение вида А: каноническим уравнением окружности с центром в точке С (а; в) и радиусом R; В: уравнением, позволяющем определить расстояние между двумя точками; С: нормальным уравнением прямой; D: уравнением параболы. 22. Для того чтобы уравнение второго порядка определяло окружность необходимо, чтобы А: в уравнении второго порядка отсутствовал свободный член; В: в уравнении второго порядка не было слагаемых содержащих квадраты х и у; С: в уравнении второго порядка отсутствовало слагаемое, содержащее произведение ху, а коэффициенты при квадратах х и у были равны; D: уравнение второго порядка не содержало переменную х. 23. Какую линию на плоскости определяет уравнение А: окружность; В: гиперболу; С: параболу; D: эллипс. 24. Эллипсом называется А: частный случай окружности; В: геометрическое место точек сумма расстояний до которых от двух фиксированных точек плоскости называемых фокусами,есть величина постоянная большая, чем расстояние между фокусами; С: геометрическое место точек разность расстояний до которых от двух фиксированных точек плоскости называемых фокусами,есть величина постоянная меньшая, чем расстояние между фокусами; D: геометрическое место точек равноудаленных от двух данных прямых. 25. Коэффициентом сжатия эллипса называется А: отношение малой полуоси эллипса к его большой полуоси; В: отношение малой оси эллипса к расстоянию между его фокусами; С: отношение расстояния между фокусами к длине большой оси эллипса; D: отношение большой полуоси эллипса к малой полуоси эллипса.
26. Эксцентриситетом эллипса называется А: отношение малой полуоси эллипса к его большой полуоси; В: отношение малой оси эллипса к расстоянию между его фокусами; С: отношение расстояния между фокусами к длине большой оси эллипса; D: отношение коэффициента сжатия эллипса к расстоянию между фокусами. 27. Эксцентриситет эллипса характеризует А: форму эллипса; В: расположение его фокусов; С: расстояние до директрисы; D: отношение полуосей. 28. Гиперболой называется (должно быть выбрано не менее двух ответов) А: график прямойпропорциональности; В: геометрическое место точек сумма расстояний до которых от двух фиксированных точек плоскости называемых фокусами,есть величина постоянная большая, чем расстояние между фокусами; С: геометрическое место точек абсолютная величина разности расстояний до которых от двух фиксированных точек плоскости называемых фокусами,есть величина постоянная меньшая, чем расстояние между фокусами; D: график обратной пропорциональности 29. Какую линию на плоскости задает уравнение А: окружность; В: гиперболу; С: параболу; D: эллипс. 30. Прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат называется А: асимптотой; В: директрисой; С: осью симметрии; D: биссектрисой. 31. Эксцентриситетом гиперболы называется А: отношение малой полуоси гиперболы к ее большой полуоси; В: отношение малой оси гиперболы к расстоянию между ее фокусами; С: отношение расстояния между фокусами к длине большой оси гиперболы; D: отношение коэффициента сжатия гиперболы к расстоянию между фокусами. 32. Параболой называется А: геометрическое место точек, расстояние каждой из которых от данной точки, называемой фокусом, равно расстоянию от данной прямой, называемой директрисой; В: график прямой пропорциональности; С: геометрическое место точек разность расстояний до которых от двух фиксированных точек плоскости называемых фокусами, есть величина постоянная меньшая, чем расстояние между фокусами; D: геометрическое место точек равноудаленных от двух данных прямых. 33. Уравнение А: симметричную оси абсцисс, ветви которой направлены влево, а вершина совпадает с началом координат; В: симметричную оси абсцисс, ветви которой направлены вправо, а вершина совпадает с началом координат; С: симметричную оси ординат, ветви которой направлены влево, а вершина совпадает с началом координат; D: симметричную оси ординат, ветви которой направлены вправо, а вершина совпадает с началом координат. 34. Уравнение А: окружность с центром в точке (а; в); В: параболу с вершиной и точке (а; в) директриса которой параллельна оси абсцисс; С: эллипс; D: гиперболу. 35. Параметр параболы определяет А: расстояние между фокусом параболы и ее директрисой; В: фокальный радиус произвольной точки параболы; С: расстояние между ветвями параболы; D: ось симметрии параболы. ИТОГОВОЕ ТЕСТИРОВАНИЕ Направление подготовки 44.03.02 Психолого-педагогическое образование
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.43.109 (0.007 с.) |

 Определите координаты точки А
Определите координаты точки А определяется (должно быть выбрано не мненее двух ответов)
определяется (должно быть выбрано не мненее двух ответов) позволяют определить
позволяют определить позволяет определить
позволяет определить позволяет определить
позволяет определить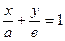 является
является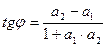 определяется
определяется называется
называется является
является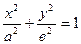

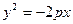 определяет параболу
определяет параболу определяет
определяет


