
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение производной функции
Определение. Производной функции у = f (x) в точке х 0 называется предел отношения приращения функции ∆ у в точке х 0 к приращению аргумента ∆ х, когда последний стремится к нулю. Таким образом, если у = f (x) - функция от х, то производная f' (x) этой функции при данном значении х определяется равенством f' (x) = Пример. Исходя из определения, найти производную функции у = Решение. Найдем приращение функции: ∆ у = Составим отношение приращения функции к приращению аргумента:
Считая х фиксированным числом, найдем предел данного отношения когда ∆ х стремится к нулю: у' = Тогда у' (4) = Ответ: у' (4) =
Производные основных элементарных функций Формулы дифференцирования основных элементарных функций сведены в таблицу:
Производная суммы, произведения и частного Пусть U и V – две функции, определенные на одном и том же промежутке. Тогда производная суммы этих функций равна сумме их производных, если они существуют, т.е. (U + V)' = U ' + V '. Эта формула справедлива для любого конечного числа слагаемых: (U 1 + U 2 + U 3 +…+ Uk)' = U' 1 + U' 2 + U' 3 +…+ U'k. Если производные функций U и V существуют, то производная их произведения вычисляется по формуле: (U·V)' = U '· V + U · V '. Постоянный множитель можно выносить за знак производной: (k f(x))' = k f ' (x). Если функции U и V имеют в точке х производные и V ≠ 0, то в этой точке существует производная их частного
Частные случаи:
Пример. Пользуясь формулами дифференцирования, найти производную функции у = Решение.
у ' = Ответ: у ' =
Производная сложной функции Пусть у = f (u) и u = φ (x). Тогда у есть сложная функция x: у = f [ φ (x)], а переменная u – промежуточный аргумент. В этом случае нахождение производной у'х осуществляется в соответствии со следующей теоремой. Теорема. Если функция u = φ (x) имеет производную u ' х в точке х, а функция у = f (u) имеет производную у'и в соответствующей точке и, то сложная функция у = f [ φ (x)] в данной точке х имеет производную у'х, которая находится по следующей формуле:
у'х = у'и · u ' х. Иными словами: производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента. Пример. Найти производную функции у = Решение. Дана сложная функция у = Применяя теорему, получаем: у ' = ( Ответ: у ' =
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.239.195 (0.005 с.) |
 .
. в точке х = 4.
в точке х = 4. .
. =
=  .
. =
=  =
=  = =
= =  =
=  = =
= =  =
=  .
. =
= 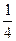 .
. ;
IV¢. у = ln x; у ' =
;
IV¢. у = ln x; у ' =  ;
;
 ;
VIII. у = ctg x; у' = –
;
VIII. у = ctg x; у' = –  ;
;
 ;
X. у = arccos х; у' = –
;
X. у = arccos х; у' = –  ;
XII. у = arcсtg x; у' = –
;
XII. у = arcсtg x; у' = –  , которая вычисляется по формуле:
, которая вычисляется по формуле: .
. ;
;  ;
;  (х ≠ 0).
(х ≠ 0). .
. = =
= =  =
=  = =
= =  .
. .
. , и = 2 х + х 2.
, и = 2 х + х 2. ·(2 х + х 2)' =
·(2 х + х 2)' =  = =
= =  .
.


