
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие определенного интеграла. Простейшие свойства определенного интеграла
Интегралом от а до b функции f (x) называется приращение первообразной F (х) этой функции, т.е. F (b) – F (а). Интеграл от а до b функции f (x) обозначается
Простейшие свойства определенного интеграла 1. При перестановке пределов меняется знак интеграла
2. Интеграл с одинаковыми пределами равен 0
3. Отрезок интегрирования можно разбивать на части
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых. 5. Постоянный множитель можно выносить за знак интеграла. Формула Ньютона-Лейбница Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона – Лейбница.
Определенный интеграл равен разности значений неопределенного интеграла при верхнем и нижнем пределах интегрирования. Пример. Вычислить интеграл Решение.
Ответ: 2 Площадь плоской фигуры Площадь всякой плоской фигуры, отнесенной к прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох или оси Оу. Площадь криволинейной трапеции вычисляется по формуле: S = В том случае, когда непрерывная функция f (x) ≤ 0 на отрезке [ а; b ], площадь соответствующей криволинейной трапеции вычисляется по формуле S = - Если функция f (x) непрерывна на отрезке [ а; b ] и принимает на данном отрезке как положительные, так и отрицательные значения, то отрезок интегрирования разбивается на такие части, в каждой из которых функция
 
Рис. 13

Рис. 14.
Пример. Вычислить площадь фигуры, ограниченной линиями х = 4, у = х 2 – 4 х + 6, у = 2. Решение. Найдем пределы интегрирования - точки пересечения данных линий. Имеем а = 2, b = 4, причем х 2 – 4 х + 6 ≥ 2. следовательно площадь фигуры, ограниченной данными линиями равна
S = Ответ: S = 2
Объем тела вращения Если тело образуется при вращении вокруг оси Ох криволинейной трапеции прилежащей коси Ох, его объем определяется по формуле V = Если тело образуется при вращении вокруг оси Оу криволинейной трапеции прилежащей к оси Оу, его объем определяется по формуле V = Пример. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: у 2 = 2 рх, х = а вокруг оси Ох. Решение. V = Ответ: V =
٭ ٭ ٭
216. Вычислить определенные интегралы: а) b)
217. Вычислить определенные интегралы: а) b)
218. Вычислить определенные интегралы: а) b)
219. Найти площадь фигуры, ограниченной параболой у = 6 х - 220. Вычислить площадь фигуры, ограниченной линиями: а) у = 2 х + 3, у = 0, х = -1, х = 2; b) у = 5 х – 3 х 2, у = 0; с) у = d) у =
221. Вычислить площадь фигуры, ограниченной линиями: а) у = 2 sin х, у = 0, х = - π, х = 0; b) у = с) у = d) у = 2 х 2 – 2, у = 0, х = 2.
222. Вычислить площадь фигуры, ограниченной линиями: а) у = х 2, у = b) у = cos x, у = с) у = х 2 – 4, у = х – 2; d) у = sin х, у = cos x.
223. Вычислить площадь фигуры, ограниченной линиями: а) х + 4 у – 9 = 0, 2 х – 3 у + 4 = 0,3 х + у – 16 = 0; b) у = с) у = -х 2 – 2 х + 7, у = -х 2 – 4 х + 7, у = -4 х + 6; d) у = sin х, у = 2 sin x, х = 0, х = π.
224. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями: а) х 2 + у 2 = 9, х = -1; b) у = с) у = х 2 – 3, х = -2, х = 3; d) у = sin х, х = 0, х = π.
225. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями: а) у = b) у = ln x, х = 1, х = е; с) у = -х 2 – 2 х – 3, х = -1, х = 3; d) у = sin 2х, х = 0, х = 226. Вычислить объем тела, образованного вращением вокруг оси абсцисс эллипса 227. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной параболами у = х 2 и х = у 2. 228. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной окружностью х 2 + у 2 = 4 и прямой у = х.
229. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной кубической параболой у = х 3 и параболой х = у 2. 230. Вычислить объем тела, образованного вращением вокруг оси абсцисс плоской фигуры, ограниченной кривой у = sin 2х и прямой у = Глава 6. Дифференциальные уравнения
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.101 (0.02 с.) |
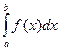 . Числа а и b называются пределами интегрирования, а – нижним, b – верхним; отрезок [ а; b ]– отрезком интегрирования.
. Числа а и b называются пределами интегрирования, а – нижним, b – верхним; отрезок [ а; b ]– отрезком интегрирования. .
. = 0.
= 0. +
+  .
.
 = F (х)
= F (х)  .
.
 =
= 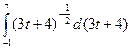 =
= 

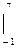 =
=  - -
- -  =
=  = 2
= 2  .
S =
.
S =  .
.

 –
– 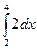 =
=  =
=  =
=  –
–  +4 х
+4 х  = =
= =  – 32 + 16 – (
– 32 + 16 – ( – 16 = 18
– 16 = 18 
 , (х 1 < х 2).
, (х 1 < х 2). , (у 1 < у2).
, (у 1 < у2). =
=  =
=  =
=  dx; с)
dx; с)  ;
; dx; d)
dx; d) 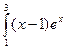 dx.
dx. dx; с)
dx; с)  dx;
dx; ; d)
; d)  dx.
dx. ; с)
; с)  ;
; dx; d)
dx; d)  dx.
dx.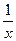 , у = 0, х = 1, х = 3;
, у = 0, х = 1, х = 3; , у = 3, х = 0.
, у = 3, х = 0. , у = 0, х = 1, х = 6;
, у = 0, х = 1, х = 6; х – 1, у = 0, х = 0, х = 6;
х – 1, у = 0, х = 0, х = 6; , у = 0, х = 3;
, у = 0, х = 3; ;
; , х = 1, х = е;
, х = 1, х = е; .
. х.
х.


