
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных уравнений и их решениеСодержание книги
Поиск на нашем сайте
3.1. Решение систем линейных уравнений методом последователь-ного исключения неизвестных (методом Гаусса). В основе метода Гаусса лежат элементарные преобразования над системой линейных уравнений, приводящих данную систему к такому виду, из которого все ее решения находятся непосредственно. Рассмотрим систему m линейных уравнений с n неизвестными: а 11 х 1 + а 12 х 2 +... + а 1 п хп = b 1, а 21 х 1 + а 22 х 2 +... + а 2 п хп = b 2, ............ ат 1 х 1 + ат 2 х 2 +... атпхп = bm. Возможны два случая. 1) Среди уравнений системы имеется такое, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, т.е. уравнение 0 ∙ х 1 + 0 ∙ х 2 +... + 0 ∙ хп = b, где b – число отличное от нуля. В этом случае никакой набор значений х 1, х 2, х 3,..., хп не может удовлетворять такому уравнению, поэтому система уравнений несовместна. 2) В каждом уравнении системы хотя бы один из коэффициентов при неизвестных отличен от нуля. Для определенности положим а 11 ≠ 0. исключим х 1 из всех уравнений системы начиная со второго. Для этого из второго уравнения вычтем первое, умноженное на а 11 х 1 + а 12 х 2 +... + а 1 п хп = b 1, а ......... а Положив а а 11 х 1 + а 12 х 2 + а 13 х 3 +... + а 1 п хп = b 1, а а ......... а Продолжая этот процесс, мы обязательно придем к одному из двух случаев. I. Либо после какого-то шага получится система, содержащая уравнение вида 0 ∙ х 1 + 0 ∙ х 2 +... + 0 ∙ хп = b, где b – число отличное от нуля. Тогда исходная система уравнений несовместна. II. Либо мы придем к системе вида а 11 х 1 + а 12 х 2 +... + а 1k хk +... + а 1 п хп = b 1, а .............. а где k ≤ n. а) Если k = n, то система принимает вид а 11 х 1 + а 12 х 2 +... + а 1k хk = b 1, а .......... а и имеет единственное решение. б) Если k < n, то система имеет бесконечное множество решений. При этом, придавая различные значения переменным хk+1, хk+2, ..., хп, получаем различные значения переменных х1, х2, х3,..., хk. Практически процесс решения системы линейных уравнений можно облегчить, если вместо преобразований над системой производить преобразования над её расширенной матрицей:
Пример: Решить систему уравнений методом последовательного исключения неизвестных: 3 х 1 - х 2 + 2 х 3 – 3 х 4 = -2, х 1 + 3 х 2 – х 3 + 2 х 4 = 2, 2 х 1 + х 2 – 5 х 3 – х 4 = -1, -5 х 1 + х 3 + х 4 = -3. Решение. Данной системе соответствует расширенная матрица:
~ Последней матрице соответствует система: х 1 + 3 х 2 – х 3 + 2 х 4 = 2, 5 х 2 + 3 х 3 + 5 х 4 = 5, 11 х 3 + х 4 = 2, -2 Из полученной системы находим: х 4 = 2; х 3 = 0; х 2 = -1; х 1 = 1. Ответ: х 1 = 1; х 2 = -1; х 3 = 0; х 4 = 2.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.55.63 (0.006 с.) |

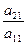 , затем аналогично поступим с третьим, четвертым и всеми оставшимися уравнениями системы. В результате этих преобразований система примет вид:
, затем аналогично поступим с третьим, четвертым и всеми оставшимися уравнениями системы. В результате этих преобразований система примет вид: х 2 +... + а
х 2 +... + а  хп = b
хп = b 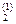 ,
,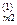 х 2 +... а
х 2 +... а  хп = b
хп = b  .
.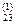 х 3 +... + а
х 3 +... + а  х 3 +... + а
х 3 +... + а  хп = b
хп = b 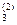 ,
, х 3 +...+ а
х 3 +...+ а  хп = b
хп = b 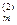 .
.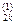 х k +...+ а
х k +...+ а 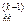 хk +...+ а
хk +...+ а 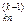 хп = b
хп = b 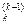 ,
,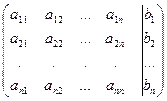
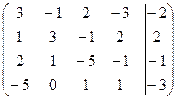 ~
~ 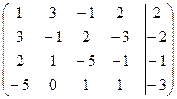 ~
~ 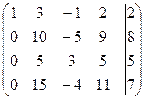 ~
~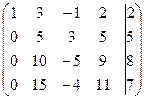 ~
~  ~
~ 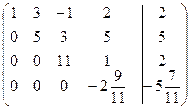 .
.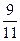 х 4 = -5
х 4 = -5 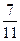 .
.


