
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее уравнение динамики Даламбера-ЛагранжаСодержание книги
Поиск на нашем сайте
Принцип возможных перемещений также к системе находящихся в движение. Расмотрим систему точек с идеальными связями. Тогда Где Иначе:
К – той точки возможное измещение
т.к
В случае равновесия сил, обобщенная сила всех заданных сил равна нулю, т.е.
При равновесии консервативной системы обобщенная сила равна частной производной от потенциальной энергии; по обобщенным координатам равна нулю. Однако системы могут иметь несколько равновесных положений. Положение А является устойчивым равновесием, так как при малых отклонениях система вернётся в исходном положении. Если не вернётся (В), то равновесие неустойчивое.
 С точки зрения потенциальной энергии, устойчивое равновесие будет тогда, когда П имеет min. С точки зрения потенциальной энергии, устойчивое равновесие будет тогда, когда П имеет min.
Критерий минимума функции П:
Критерий устойчивости равновесия:
(2) формула выражает теорему Лагранжа-Дирихле об устойчивости равновесия консервативной системы с одной степенью свободы. Если система имеет s -степеней свободы, то там устойчивое равновесие определяется критерием Сильвестра.
ТЕОРИЯ МАЛЫХ КОЛЕБАНИЙ
Теорема малых колебаний, начав свое развитие с изучения движения маятника, превратилась в самостоятельную дисциплину, с весьма сложным математическим аппаратом. Развитие вычислительной техники дало возможность решать очень большой класс задач для систем с n -степенями свободы. Для описания колебательных процессов и их количественной оценки, динамических характеристик, необходимо определиться с равновесным, устойчивым состоянием системы. Пример определения равновесия системы и исследование на устойчивость. Определение критериев устойчивости
Дано: ОА=ОВ= ℓ; с – коэффициент жесткости пружины, ℓ -длина нерастянутой пружины.
П=П1+П2= Удлинение пружины составляет
Потенциальная энергия системы равна П= Т.к. равновесие в системе будет при условии
очевидно, что равенство справедливо в двух случаях: 1) 2)
Эти равновесные положения исследуем на устойчивость: 1) 2) при
Потенциальная и кинетическая энергия системы в обобщенных координатах Гармонические колебания Для системы с s -степенью свободы потенциальная энергия, есть функция обобщенных координат
Разложим ее в ряд Маклорена по степеням q: П(q1….q5)=П(0)+ Учитывая, что
то
или сокращенно
где с - обобщенный коэффициент жесткости системы или квазирующий коэфициент. Аналогично, рассматривая кинетическую энергию системы, получаем:
где а - обобщенный коэффициент инерции системы. Рассмотрим движение системы, которое возможно относительно равновесного положения, т.е. составим дифференциальное уравнение движения:
если
то по уравнению
Правая часть уравнения Лагранжа:
Уравнение (1) - уравнение свободных или гармоничных колебаний.
или
где А – амплитуда. При t =0:
Получаем уравнение амплитуды:
Период колебаний равен
Независимость периода от амплитуды – изохронность колебаний. Пример: А=
П =
Подставим П и Т, или
где с - жесткость рессора.
Затухающее колебание Диссипативная функция Релея
В реальных условиях на любую систему действует сопротивления различного характера (трение, сопротивление среды), поэтому гармонические колебания не встречаются и колебания любой системы будут являться затухающими. Поскольку сила сопротивления среды i –той точки системы противоположна и пропорциональна скорости, то сопротивление R будет равно:
где Происходит потеря кинетической энергии (рассеивание или диссипация), колебания для этой точки, тогда вводится диссипативная функция Релея
где b – обобщенный коэффициент диссипации. Тогда обобщенная сила сопротивления равна:
Таким образом, получим соответствующие уравнения:
Тогда:
Делим на а и получаем:
Введем обозначением:
где n - коэффициент затухания. Тогда для уравнения затухающих колебаний:
Общий интеграл уравнения (2)
где А - амплитудное значение затухающих колебаний;
Частота колебаний равна
На графике колебаний:
Период равен
Если
На этом основано действие автомобильных амортизаторов.
Выбираем обобщение координат
1) определим кинетическую энергию системы:
2) потенциальная энергия системы равна
Т.к
то
3) в положении равновесии
Подставляя полученное выражение (2) в (1), получим значение потенциальной энергии П в положении равновесия П=
Сравнивая полученные выражения (1) и (3) с выражениями
определяем значения коэффициентов а и с. Частота таких колебаний находится по формуле
Но этого для решения задачи недостаточно, так как надо получить дифференциальное уравнение движения и определить, колебания являются гармоническими или затухающими. Используя уравнения (1) и (3), получим уравнение типа
Колебания затухающие, тогда частота равна
Следовательно, определяем n и k
Вынужденные колебания
Предположим, что на систему в определенной точке действует периодически изменяющаяся сила с частотой ω:
где F – возмущающая сила; ω – частота этой силы; H – амплитудное значение; θ – начальная фаза. Тогда система будет совершать вынужденные колебания и поведение системы будет определяться в основном наличием сопротивления и частоты возмущающей силы Тогда уравнение Лагранжа запишется:
где QR – обобщенная сила сил сопротивления; QF – обобщенная сила сил возмущения. Дифференциальное уравнение будет выглядеть:
Уравнение (1) – дифференциальное уравнение вынужденных колебаний при наличии сил сопротивления. Если сопротивление отсутствует, то n =0. Тогда система будет совершать гармонические колебания с частотой ω, но не с k. Текущая амплитуда при наличии сил находится по формуле
Если сопротивление отсутствует (т.е. n =0), то амплитуда равна
Если отсутствует сопротивление частоты собственных колебаний совпадают с частотой вынуждающих сил (
Свойства вынужденных колебаний
1. Вынужденные колебания при линейном сопротивлении являются незатухающими с постоянной амплитудой. 2. Сопротивление не влияет на частоту вынужденных колебаний, которые совпадают с частотой возмущающей силы. 3. Вынужденные колебания при линейном сопротивлении не зависят от начальных условий. 4. Резонанс ( Теория удара
В результате действия на систему обычных не ударных сил за ничтожно малый промежуток времени скорость отдельной точки тела будет изменяться на бесконечно малую величину
Явление, при котором за ничтожно малый промежуток времени скорости точек тела изменяются на конечную (заметную) величину, называется ударом. Если скорость точки тела до удара
где τ – время удара;
Так как при ударе развиваются очень большие силы, то берется среднее значение ударной силы.
где В теории удара принимается ряд допущений: 1. действием неударных сил пренебрегают; 2. не учитывается перемещение тела в процессе удара; 3. результат действия ударной силы на тело выражается в конечном изменении вектора скорости. Суммируя по n -точкам системы, получим теорему об изменении количества движения при ударе
где Если внешний удар равен нулю, то К=Ко=const, т.е. имеет место закон сохранения количества движения системы при ударе.
Коэффициент восстановления Величина ударного импульса зависит не только от масс и скоростей соударяемых тел, но и от упругих свойств этих тел, которые характеризуются коэффициентом восстановления
в процессе удара произошла потеря энергии, которая затрачивается на остаточную деформацию тела, на выделение тепла, на образование звука… поскольку
Самый высокий коэффициент восстановления у стекла - 15/16; у стали - 5/9; у дерева - ½. Если в течение удара нет фазы восстановления после удара (K =0), то это - абсолютно неупругий удар (к примеру – пластилин). Если h=H, т.е. K=1 – это абсолютно упругий удар, что не реально на практике. Если
Скорость удара будет Различаться и обусловленое Формулой тел.
Теорема об изменении кинетического момента системы при ударе
При ударе изменение кинетического момента равно сумме моментов внешних ударных импульсов:.
Центр удара
Если поменять местами оси привеса и качания, то период не изменится (теорема Гюйгенса). Точка К – центр удара. Если внешний удар приходится в точку К, то отсутствуют динамические составляющие реакции шарнира. Примечание: для стержня длиной l центр удара приходится на h=2/3l Приведённая длина физического маятника соответствует расстоянию от оси привеса до центра удара и определяется по формуле
Рекомендованные темы для самостоятельного изучения динамики системы; не вошедшую в учебную практику: 1. Движение тел, перемещение массы. Формула Циолковского. Уравнение Мещерского. 2. Приближенная теория гироскопа. Навигационные системы. 3. Задачи оптимизации процессов и конструкций методом множителя Лагранжа. 4. Движение системы с n -степенями свободы. Элементы робототехники. 5. Электронные аналоговые машины.
В разработке электронной версии курса лекций по теоретической механике (динамика) принимали участие студенты групп: 03-А-АД 1- Брагин Д. И., 04-А-АД 2 - Филин А., 04-А-АД 3 -Ляшко В. Г.
Рецензент: доктор технических наук, заведующий кафедрой теоретической механики, профессор Смелягин А. И .
Краснодар, 2006 год
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.54.61 (0.01 с.) |

 к- этой точки момент записать:
к- этой точки момент записать: 
 и
и  - равнодействующих активных сил и динамических реакций связи.
- равнодействующих активных сил и динамических реакций связи.
 , заменяем уравнение возможных работ всей системы.
, заменяем уравнение возможных работ всей системы. и
и 
 , для идеальных связей.
, для идеальных связей.
 ;
; 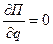

 (1)
(1) (2)
(2) Потенциальная энергия системы равна
Потенциальная энергия системы равна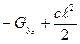
 =…..=
=…..= 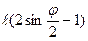
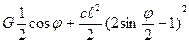
 = 0
= 0


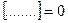 откуда:
откуда:

 при
при 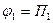
 откуда:
откуда: 


 откуда
откуда 






 ,
, ,
,
 ; П=
; П=  ,
,



 ; тогда
; тогда или
или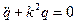 (1)
(1) характеризует циклическую частоту собственных колебаний системы, которые зависят от жесткости системы с и инерционности.
характеризует циклическую частоту собственных колебаний системы, которые зависят от жесткости системы с и инерционности. (2)
(2)
 , (3)
, (3)




 Найти частоту собственных колебаний балки.
Найти частоту собственных колебаний балки.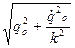 ;
; 









 - коэффициент пропорциональности, характеризует свойства среды.
- коэффициент пропорциональности, характеризует свойства среды. ,
,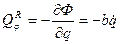
 П=
П= 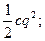





 (1)
(1)
 ;
;  ,
, (2)
(2) ,
, - начальная фаза колебания.
- начальная фаза колебания.
 - декремент затухания, -nt - логарифм декремента затухания.
- декремент затухания, -nt - логарифм декремента затухания.
 График затухающих колебаний имеет вид
График затухающих колебаний имеет вид , то нет полного цикла колебаний (лимитационное колебание)
, то нет полного цикла колебаний (лимитационное колебание)

 Пример: определить частоту, период колебаний передней подвески автомашины.
Пример: определить частоту, период колебаний передней подвески автомашины.


 ;
; 
 (1)
(1)
 (2)
(2) =
=  (3)
(3)


 ;
; 






 ;
; 
 ,
, .
. ,- Фр обобщеных сил (заданых сил)
,- Фр обобщеных сил (заданых сил)
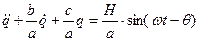
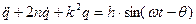 (1)
(1)

 ), то наступает явление резонанса и амплитуда неограниченно возрастает (А → ∞). Конструкция разрушается.
), то наступает явление резонанса и амплитуда неограниченно возрастает (А → ∞). Конструкция разрушается. ) наступает при отсутствии (малом) сопротивлении и совпадении частот k и ω.
) наступает при отсутствии (малом) сопротивлении и совпадении частот k и ω.
 , а после удара
, а после удара  , то используется теорема об изменении количества движения:
, то используется теорема об изменении количества движения: ;
;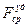 - среднее значение ударной силы.
- среднее значение ударной силы.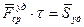 ,
,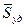 - ударный импульс
- ударный импульс ,
, - сумма внешних ударных импульсов (внешних ударов).
- сумма внешних ударных импульсов (внешних ударов).
 ;
; 

 т.к
т.к ;
;  , то:
, то:
 - то это не вполне упругий удар.
- то это не вполне упругий удар. При ударе угол падения не равен углу отражения.
При ударе угол падения не равен углу отражения.

 На коэффициент восстановления тела K влияет и форма тела, а не только масса m и скорость V, т.к. происходит изменение условий распределения ударной волны в самом теле, что приводит к изменению упругих свойств самого тела.
На коэффициент восстановления тела K влияет и форма тела, а не только масса m и скорость V, т.к. происходит изменение условий распределения ударной волны в самом теле, что приводит к изменению упругих свойств самого тела. т.к
т.к  то
то Т.е. изменение угловой скорости тела при вращение вокруг оси Z вследствие удара прямо пропорциональна моменту ударного импульса относительно оси и обратно пропорциональна моменту инерции тела относительно точки оси.
Т.е. изменение угловой скорости тела при вращение вокруг оси Z вследствие удара прямо пропорциональна моменту ударного импульса относительно оси и обратно пропорциональна моменту инерции тела относительно точки оси.



