
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрия масс. Теорема о движении ценра масс Механической системы.Содержание книги
Поиск на нашем сайте
Рассмотрим систему материальных точек массы которых Радиус-вектор
Проектируя (1) на оси координат: Из (1) получим:
Суммируя его к точкам системы и учитывая, что
Тогда уравнение (2) запишется:
Эта формула выражает теорему о движении центра масс механической системы: Центр масс механической системы движется как материальная точка, к которой приложены все внешние силы.
Следствие: Если Следствие выражает закон сохранения покоя или равномерное прямолинейное движение центра масс В проекции на ось координат:

Xe= Система состоит из двух объектов и находится в покое Дано: m Найти:
Т. к.
Кинетический момент точки и систем Теоремы об изменении момента количества движения материальной точки и системы Теорема моментов До сих пор мы вычисляли момент силы относительно некоторого неподвижного центра О.
где Аналогично вычислим момент количества движения точки относительно неподвижного центра О:
Установим зависимость кинетического момента точки и момента силы F, действующей на нее. Для чего продифференцируем
Векторная производная от кинетического момента точки по времени равна моменту силы, действующей на нее относительно той же неподвижной точки О. Если момент силы равен нулю, то кинетический момент остается постоянным, что выражает закон сохранения кинетического момента:
Груз веса Р двигается по окружности радиуса Найти
При изменении КИНЕТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ
Рассмотрим систему материальной точки и выберем точку Мk массой mк,скорость которой Vk, на нее действуют внешние и внутренние силы ; ↓ ↓
Тогда:
Следствие: закон сохранения кинетического момента системы: если
Кинетический момент твердого тела при вращении вокруг неподвижной оси Вычислим Для всего тела: Здесь Следовательно
Для демонстрации закона сохранения кинетического момента системы представлена платформа Жуковского: ℓ→R

Дано: Найти: при переходе точки на край диска
I.
↓ ↓
Т. к..
II. Если Если
Здесь: 2) ↓ ↓
3)

|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.217.86 (0.006 с.) |

 и
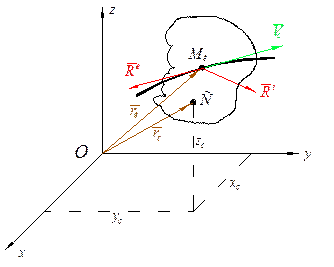
и  .Положение
.Положение  точки определима радиуса – вектором
точки определима радиуса – вектором  , а точки С – вектором
, а точки С – вектором  .
. можно определить по формуле:
можно определить по формуле:  (1), где
(1), где  - масса тела.
- масса тела. ,
,  ,
, 

 Уравнение движения К-той точки запишется:
Уравнение движения К-той точки запишется:  (2)
(2) , то получим левую часть уравнения (2):
, то получим левую часть уравнения (2):

 т.е все внешние силы уравновешиваются, тогда
т.е все внешние силы уравновешиваются, тогда  ,→
,→  .
.

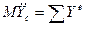 (5)
(5)

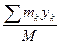
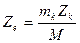
 m2
m2  Vo =0 m2 =
Vo =0 m2 = 
 при смещении груза
при смещении груза  на
на  .
.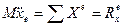

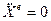



 , то определяем S1=
, то определяем S1=  ……… (м)
……… (м) (1)
(1) - радиус, вектор точки, проведенный из неподвижного центра О.
- радиус, вектор точки, проведенный из неподвижного центра О. - выражает кинетический момент точки и аналогично моменту
- выражает кинетический момент точки и аналогично моменту  запишем:
запишем: 



 по t:
по t: по:
по: 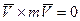 т.к. (
т.к. ( )
) , следовательно:
, следовательно: (3)
(3)
 т.е.
т.е.  . В координатной форме:
. В координатной форме: 


 , а затем на расстоянии
, а затем на расстоянии  от Z
от Z и
и 
 , т. к.
, т. к.  , то
, то  . Т. е.
. Т. е. 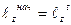 или
или через
через 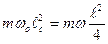

 и
и  . Тогда для системы и точек:
. Тогда для системы и точек: =
=  К=1…….n
К=1…….n кин.мом.сист.
кин.мом.сист.  -главный момент внешних сил
-главный момент внешних сил -главный момент внутренних сил равен 0
-главный момент внутренних сил равен 0 (7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра.
(7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра. (4) в координатной форме:
(4) в координатной форме: 

 (главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная.
(главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная. т.е.
т.е.  (5)
(5) для точки массой m:
для точки массой m: 

 -момент инерции тела.
-момент инерции тела.
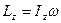 кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость.
кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость. 

 т.е.
т.е. 
 =
= 



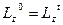 , то:
, то:  ,
, 
 не равен 0:
не равен 0: пусть
пусть 
 интегрируя:
интегрируя:
 (2) В момент t сек точка массой
(2) В момент t сек точка массой  переходит в положение В, имея при этом относительную скорость
переходит в положение В, имея при этом относительную скорость  , тогда
, тогда

 (3), где
(3), где  т. к.
т. к.  получаем
получаем 


