
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическая теорема КориолисаСодержание книги
Поиск на нашем сайте
До сих пор мы рассматривали движение несвободной точки по отношению к неподвижной инерциальной системе отсчета, в которой законы динамики выполняются с достаточной точностью, а также система связана с Землей, которую условно считают неподвижной. Рассмотрим теперь движение несвободной точки по отношению к подвижной системы отсчета и установим основное уравнение динамики относительного движения несвободной материальной точки. Пусть P – заданная сила, N - динамическая реакция связи. Координаты точки в подвижной системе -
Если рассмотрим движение точки в подвижной системе, то, как известно из кинематики, точка будет находиться в сложном движении, и если движение подвижной системы не будет поступательным, то ускорение
Подставим уравнение (2) в (1) и, так как нас интересует динамика относительного движения, то в левой части уравнения (1) оставим
Обозначим: - -
Тогда дифференциальное уравнение относительного движения запишется:
Таким образом, отмечаем в случае непоступательного переносного движения подвижной системы отсчета относительное движение точки происходит также, как и абсолютное (в соответствии с Причем: инерционные силы не являются результатом воздействия других тел на точку, а являются следствием наличия движения системы отсчета
Формула (3) выражает динамическую теорему Кориолиса.
ЧАСТНЫЕ СЛУЧАИ 1) Переносное движение
2) Переносное движение – равномерное вращение:
3) Переносное движение неравномерное (поступательное):
4) Переносное движение равномерное; прямолинейное поступательное: т.к.
и тогда:
т.е. при переносном поступательном равномерном и прямолинейном движении системы относительное движение несвободной точки в этой системе происходит также как и в неподвижной системе, т.к. описываются одинаковыми уравнениями (4) и (1). Все механические явления в системе отчет, которые движутся по отношению к неподвижной системы равномерно, прямолинейно, поступательно происходит также как и в неподвижной системе и никакими методами и измерениями,(наблюдениями) нельзя обнаружить движение подвижной системы. (Принцип относительной классической механики Галилея).
Если
В случае относительного покоя несвободной материальной точки она находится в динамическом равновесии под воздействием заданных сил (равнодействующая
При
НЕВЕСОМОСТЬ материальной точки – отсутствие давления этой точки на каждое из тел с которым оно может соприкасаться. Система отсчета в которой наблюдается невесомость называется собственной системой отсчета, в ней выполняются условия: главный вектор и главный момент относительно любого центра приведения равны 0. Это соотношение можно создать искусственно в самолете.
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ И СИСТЕМЫ
Две основных меры механического движения и действия силы. Импульс силы. Теорема импульсов.
Динамика рассматривает 2 случая преобразования механического движения; 1)механическое движение формально переносится с одной системы на другую в результате непосредственного взаимодействия (соударение бильярдных шаров). 2)Механическое движение превращается в другую форму материи (тепло). Многолетний спор по поводу мер механического движения закончил Ф. Энгельс: *мера движения в первом случае * Мера механического действия силы- импульс (S) *Во втором случае – кинетическая энергия
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 3243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.178.122 (0.008 с.) |

 . По теореме Кориолиса:
. По теореме Кориолиса:


 (1)
(1) по теореме Кориолиса (абсолютное ускорение) будет представляться
по теореме Кориолиса (абсолютное ускорение) будет представляться (2),
(2),



 переносная сила инерции
переносная сила инерции кориолисова сила инерции
кориолисова сила инерции (3)
(3) ) и плюс переносная и кориолисова силы инерций.
) и плюс переносная и кориолисова силы инерций. , которая сообщает точке переносное и кориолисово ускорение, которое в свою очередь провоцируют появление сил инерции.
, которая сообщает точке переносное и кориолисово ускорение, которое в свою очередь провоцируют появление сил инерции.
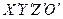 - не равномерное вращение
- не равномерное вращение
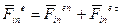


 т.е. справедливо равенство (3)
т.е. справедливо равенство (3)









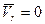 ,
,  ,
,  ,
,  , то
, то  , тогда уравнение (3) примет вид:
, тогда уравнение (3) примет вид:
 ), динамической реакции связи (равнодействующая
), динамической реакции связи (равнодействующая  ) и переносной силы инерции (
) и переносной силы инерции ( ), геометрическая сумма которых равна нулю, и выражает принцип Даламбера для несвободной материальной точки.
), геометрическая сумма которых равна нулю, и выражает принцип Даламбера для несвободной материальной точки. , получим N=0, т. е. состояние невесомости
, получим N=0, т. е. состояние невесомости - количество движения.
- количество движения. (Нсек)
(Нсек)
 - мера действия силы - работа A= Р∙Х (Нм)
- мера действия силы - работа A= Р∙Х (Нм)


