
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Германа-Эйлера-Даламбера для несвободной материальной точки
(«Петербургский принцип»)
Для свободной материальной точки массой m использовали уравнение вида
Рассмотрим движение несвободной материальной точки в трехмерной системе отсчета инерциальной системе координат.
и в соответствии со вторым законом Ньютона ускорение В результате возникновения ускорения точка массой m в соответствии с законом равенства действия и противодействия будет сопротивляться навязыванию ей ускорения с силой, равной и противоположно направленной
И тогда геометрическая сумма заданных сил
Это уравнение выражает принцип Даламбера для несвободной точки. Уравнение (1) получали ранее, рассматривая динамику относительного движения точки. Следует отметить, что Частные случаи
Тогда:
 . .
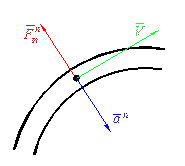
Проектируя равенство (1) на нормаль, получим:
откуда
если N=0, то наступает состояние невесомости,
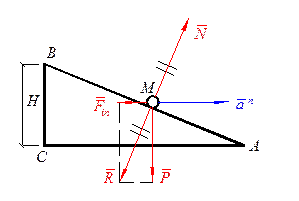
где: Пример 2. Определим угол наклона профиля автострады на вираже радиуса Р при скорости V и массе m.
Из подобия треугольников ABC и PRFin
откуда находим Н. здесь:
Принцип Даламбера для Механической системы Рассмотрим Mi -ю точку с массой mc и применим к ней принцип Даламбера:
Суммируя по n -точкам системы, получим
или
Т.е. для несвободной механической системы в любой момент времени геометрическая сумма главных векторов заданных сил, реакций связи и сил инерции равна нулю. Рассматривая разные случаи движения твердого тела, отметим, что силы инерции точек этого тела приводятся по-разному.
Частные случаи 1.Поступательное движение твердого тела Система сил инерции точек приводится к главному вектору сил инерции: где ас Если радиус-вектор i -ой точки умножить на равенство (1), то получим:
Т.е. геометрическая сумма главных вектор-моментов заданных сил, реакций связи и вектор –момента от силы инерции в любой момент времени равна нулю.
 т.е т.е
т.е. направление главного момента от сил инерции противоположно направлению углового ускорения Таким образом, при вращении тела вокруг оси силы инерции точек тела приводится только к главному моменту сил инерции относительно оси:
3. Плоско-параллельное движение Тело двигается в плоскости симметрии xoy. Ускорене центра масс В данном случае система сил инерции точек тела приводится к главному вектору сил инерции и к главному моменту от сил инерции относительно
  ; ; 
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.51.3 (0.008 с.) |
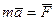
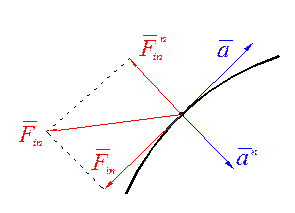
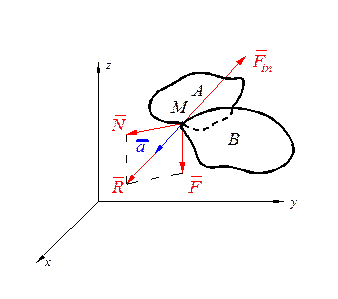 Пусть на точку действует некоторое тело А с силой
Пусть на точку действует некоторое тело А с силой  . На точку наложена связь – некоторое тело В (см. рисунок), реакция которой
. На точку наложена связь – некоторое тело В (см. рисунок), реакция которой  .Тогда равнодействующая этих сил будет находиться по формуле
.Тогда равнодействующая этих сил будет находиться по формуле
 будет направлено вдоль равнодействующей
будет направлено вдоль равнодействующей 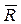 .
.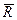 , т.е
, т.е 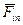 :
: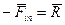
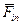 в любой момент времени равна нулю и образует уравновешенную систему сил, а точка находиться в динамическом равновесии:
в любой момент времени равна нулю и образует уравновешенную систему сил, а точка находиться в динамическом равновесии: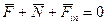 (1)
(1)

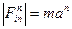 ;
; 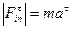
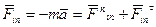
 Рассмотрим пример 1.
Рассмотрим пример 1.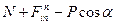 =0
=0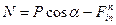
 т.е:
т.е: 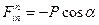 ,
,
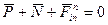
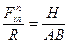 ;
;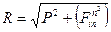 ;
;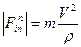

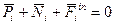
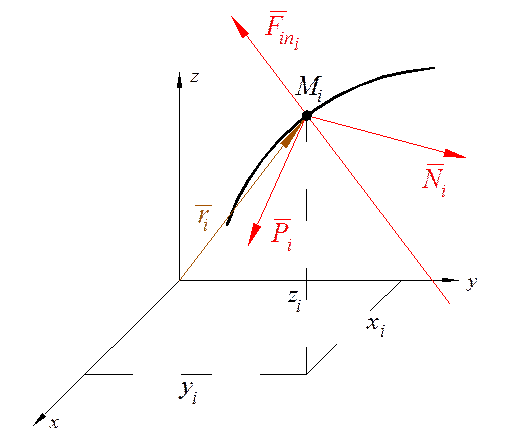
 (1)
(1)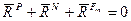
 ,
, - сумма масс всех точек;
- сумма масс всех точек;
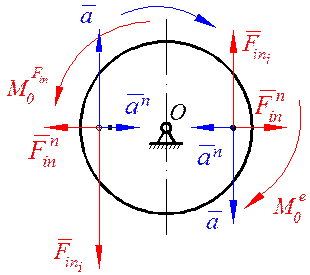 Касательное ускорение
Касательное ускорение  обеспечивается
обеспечивается  (моментом внешних сил), который равен:
(моментом внешних сил), который равен:

 .
.
 и угловое ускорение
и угловое ускорение 



