
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы динамики точки и системы
Импульс силы. Теорема о количестве движения материальной точки. Примеры.
Для характерного действия силы на точку за определенный промежуток времени вводится понятие импульса силы. Элементарный импульс В проекции на ось:
материальной точки в дифференциальной форме. Дифференциал от количества движения равен элементарному импульсу силы действия на точку за определенный промежуток времени: Интегрируя выражение (1):
Если F есть равнодействующая, то
Изменение количества движения материальной точки за определенный промежуток времени равно импульсу действующей силы за этот же промежуток времени. В координатной форме:
т.е. изменение проекции количества движения точки на ось равно проекции импульса на соответствующую ось. Пример. Дано: АВ= Найти: время t, при перемещении тела на
Если F есть равнодействующая, то

Т.к.
Vx=At Vx=
Если силы, действующие на точку, непостоянны, то
СИСТЕМА МАТЕРИАЛЬНОЙ ТОЧКИ Классификация сил действующих на систему. Дифференциальные уравнения движения системы в общем виде.
Системой материальной точки или механической системы называется такая совокупность материальных точек известным образом связанных между собой так, что движение одной из них является зависимым от остальных. Если движение такой системы не ограничено в пространстве- это свободная механическая система, если движение ограничено в одном из направлений- соответственно не свободная система. В динамике системы силы будем классифицировать как: заданные и реакции связи(динамические), а также силы внешние и внутренние(с которыми отдельные точки системы действуют друг на друга).
По свойству внутренних сил их равнодействующих, т.е. главный вектор и главный момент будут равны 0:
Потому при движении системы, определяющим фактором являются внешние силы. Дифференциальное уравнение движения системы:
n таких уравнений и является дифференциальными уравнениями системы в общем виде.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ ТЕОРИЯ ИМПУЛЬСОВ
Складывая ломанные, получаем - Количество движения - это вектор, равный геометрической сумме количества движения отдельных точек системы. Если тело или система вращаются, то для любой пары точек при вращении тела количество движения
Рассматривая К-ую точку системы с учетом действия внешних и внутренних сил:
суммируя по точкам системы, соответственно получим
Формула (1) выражает теорему о количество движения системы «К» в дифференциальной форме. Векторная производная от количества движения системы по времени равно главному вектору внешних сил
СЛЕДСТВИЕ: Закон сохранения количества движения системы: 1) Если главный вектор внешних сил равен нулю, т.е. внешние силы взаимноуравновешиваются ((
2) Если гл.вектор не равен 0, (
Изменение количества движения системы за определенный промежуток времени равен импульсу равнодействующей внешних сил. В координатной форме(например на ось Х):
ПРИМЕРЫ: Дано Vo=0 m1…mn


В момент t, за счет электродвигателя создается угловая скорость ω2, которая создает скорости V4 и V3 V4= V2- ω2 V3=R2∙ ω2 где V1скорость реагирования корпуса веса
На основании (1) Кхнач=0, то 0=
 Если Если 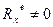 здесь здесь  , , 
если расход воды, где F - теорема в проекции на ось Х:
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.009 с.) |
 , а полный
, а полный  (Н сек)
(Н сек) ;
; 
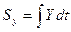 ;
;  ; так как
; так как  или:
или: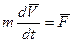
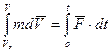
 (1)- теорема о количестве движения
(1)- теорема о количестве движения (2)
(2) - импульс равнодействующей.
- импульс равнодействующей. (5)
(5) =
=  (8)
(8)
 ; m; fтр; α; Vo=Va=0
; m; fтр; α; Vo=Va=0
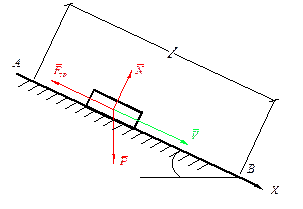
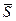 - импульс равнодействующей.
- импульс равнодействующей.
 , то
, то ;
; 

 …. секунд
…. секунд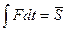 - выражается как площадь
- выражается как площадь фигуры
фигуры  ABC.
ABC. - Равнодействующая внешних сил.
- Равнодействующая внешних сил.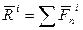 - Равнодействующая внутренних сил.
- Равнодействующая внутренних сил.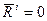

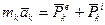 К=1……n
К=1……n
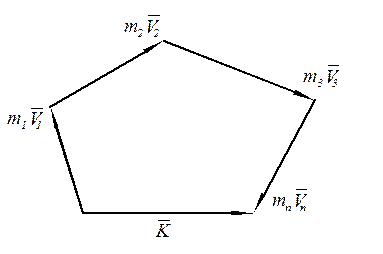
 .
. =0 и
=0 и будет определять только поступательное движение.
будет определять только поступательное движение.
 (1)
(1)
 , то количество движения системы постоянная величина,
, то количество движения системы постоянная величина, 
 . Тогда
. Тогда 


 (2) т.е.
(2) т.е. (3) если Xе=0, то проекция кол-ва движения
(3) если Xе=0, то проекция кол-ва движения 


 (1)
(1)

 отсюда находим
отсюда находим 


 т. к..
т. к.. 
 , тогда:
, тогда:  , откуда
, откуда 




