
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной Закон динамики: «произведение массы точки на ускорение, которое она получает под воздействием силы, равно по модулю этой силе, а направление силы совпадает с ускорением».Стр 1 из 7Следующая ⇒
КУРС ЛЕКЦИЙ по теоретической механике для студентов очной и заочной форм обучения
Динамика
Краснодар, 2006 г.
Введение Курс лекций составлен в соответствии с программой курса для студентов дневной формы обучения и может быть использован для самостоятельной работы над курсом студентами всех специальностей, может служить дополнением к учебнику и средством для углубленного закрепления изучаемого материала при самостоятельной работе, в том числе и для студентов заочной формы обучения. Курс лекций содержит обзор теоретических сведений, необходимых для решения задач, связанных с применением теорем динамики точки и системы. Приведены примеры решения типовых задач. ДИНАМИКА ПРЕДМЕТ ДИНАМИКИ ИСТОРИЧЕСКИЙ ОБЗОР ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ
Динамикой называется раздел механики, в котором устанавливаются и изучаются движения тел в зависимости действующих на них сил. Основоположником динамики считается Галилей (16в.). Именно он ввел понятие скорости и ускорения. Он сформулировал 1-ый закон инерции. Голландский ученый Гюйгенс ввел понятие момента инерции, центробежной силы, изобрел часы, теорию маятника. Кибальчич за неделю до своей казни, находясь в тюрьме, разработал теорию ракетного движения. Исаак Ньютон (1727г. смерти) «Математические начала натуральной философии»1687г., обобщил, объяснил и сформулировал основные законы классической механики. Установил, что количество движения системы определяется только внешними силами. Однако область применения законов Галилея-Ньютона имеет определенные ограничения: если скорости приближенны к С=3*105 м/с, то вступают в действие релятивистские законы динамики, разработанные Эйнштейном (релятивистская механика). В этой теории законы Галилея-Ньютона являются частными случаями. Огромный вклад в развитие теоретической механики также внесли: Эйлер, Циолковский, Ломоносов, Ландау, Сахаров, Басов, Прохоров, Келдыш, Королев, Крылов, Жуковский, Ляпунов, Мещерский, Ишлинский, Даламбер, Лагранж (основал аналитическую механику). В основе классической механики лежит два допущения, утверждающие существование абсолютного пространства и абсолютного времени. Предполагается, что пространство обладает чисто геометрическими свойствами, а время по Ньютону – независимо. Также допускается, что масса не зависит от скорости движения, то есть m=const.
Для удобства расчетов используется понятие «материальная точка». Это возможно тогда, когда: 1. Тело находится в поступательном движении 2. Тело мало по сравнению с траекторией (планета) В основе динамики лежат законы Галилея-Ньютона (аксиомы). Эти аксиомы выполняются в определенной системе отсчета.
Условно неподвижная система отсчета, в которой выполняются законы Ньютона, называется инерциальной. Если система подвижна, то она является неинерциальной системой. Система, связанная с центром Землиназывается геоцентрической системой координат. Система координат, связанная с центром Солнца называется гелиоцентрической. ЗАКОНЫ ДИНАМИКИ 1. Закон инерции Галилея: «материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие других тел не изменит это состояние». Иначе говоря (по Никитину): «материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчета.» Такое движение называется движением по инерции, а такая точка – изолированной. Закон Всемирного тяготения F= γ γ – гравитационная постоянная m – гравитационная масса M – инертная масса r – расстояние Классическая динамика Ньютона считает массу неизменной. Масса – количество вещества в единице объема. Сила в технической системе: 1кГс=9,8Н 1Па = 0,1кгс/м2 1Н ≈0,102кГс 1МПА = 10атмосфер 1атм. = Если Р - вес тела, а =q (ускорение свободно падающего тела) то:
Третий закон: (равенство действия и противодействия): «Силы, с которыми два материальных тела, действуют друг на друга, равны по модулю и противоположны по направлению» 4. Закон независимости действия сил: « если на материальное тело одновременно действуют несколько сил, то ускорение, которое оно получит, будет равно сумме тех ускорений, которое оно получило бы, если бы каждая сила действовала на тело отдельно».
Динамика решает две основные задачи. 1. Известен закон движения материальной точки, найти приложенные силы. 2. Основная задача динамики: известны силы - найти закон движения. Дифференциальные уравнения движения материальной точки и их интегрирование. Пример. Первая задача динамики. В неподвижной системе координат движется материальная точка массой m. Ее движение обусловлено действием некоторой силы. К-коэффициент.
М(Х; Y) Х=rcos Y= rsin
Отметим, что ∑X и ∑Y отрицательные, следовательно, F направлена к центру и называется центральной т.е.
так как r2 = ОМ2 =Х2 +У2 или Х2 +У2 - r2 = 0 – т.е. траекторией движения является окружность.
ЧАСТНЫЕ СЛУЧАИ 1) Переносное движение
2) Переносное движение – равномерное вращение:
3) Переносное движение неравномерное (поступательное):
4) Переносное движение равномерное; прямолинейное поступательное: т.к.
и тогда:
т.е. при переносном поступательном равномерном и прямолинейном движении системы относительное движение несвободной точки в этой системе происходит также как и в неподвижной системе, т.к. описываются одинаковыми уравнениями (4) и (1). Все механические явления в системе отчет, которые движутся по отношению к неподвижной системы равномерно, прямолинейно, поступательно происходит также как и в неподвижной системе и никакими методами и измерениями,(наблюдениями) нельзя обнаружить движение подвижной системы. (Принцип относительной классической механики Галилея).
Если
В случае относительного покоя несвободной материальной точки она находится в динамическом равновесии под воздействием заданных сил (равнодействующая
При
НЕВЕСОМОСТЬ материальной точки – отсутствие давления этой точки на каждое из тел с которым оно может соприкасаться. Система отсчета в которой наблюдается невесомость называется собственной системой отсчета, в ней выполняются условия: главный вектор и главный момент относительно любого центра приведения равны 0. Это соотношение можно создать искусственно в самолете.
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ И СИСТЕМЫ
Две основных меры механического движения и действия силы. Импульс силы. Теорема импульсов.
Динамика рассматривает 2 случая преобразования механического движения; 1)механическое движение формально переносится с одной системы на другую в результате непосредственного взаимодействия (соударение бильярдных шаров). 2)Механическое движение превращается в другую форму материи (тепло). Многолетний спор по поводу мер механического движения закончил Ф. Энгельс:
*мера движения в первом случае * Мера механического действия силы- импульс (S) *Во втором случае – кинетическая энергия
СИСТЕМА МАТЕРИАЛЬНОЙ ТОЧКИ Классификация сил действующих на систему. Дифференциальные уравнения движения системы в общем виде.
Системой материальной точки или механической системы называется такая совокупность материальных точек известным образом связанных между собой так, что движение одной из них является зависимым от остальных. Если движение такой системы не ограничено в пространстве- это свободная механическая система, если движение ограничено в одном из направлений- соответственно не свободная система. В динамике системы силы будем классифицировать как: заданные и реакции связи(динамические), а также силы внешние и внутренние(с которыми отдельные точки системы действуют друг на друга).
По свойству внутренних сил их равнодействующих, т.е. главный вектор и главный момент будут равны 0:
Потому при движении системы, определяющим фактором являются внешние силы. Дифференциальное уравнение движения системы:
n таких уравнений и является дифференциальными уравнениями системы в общем виде.
ТЕОРИЯ ИМПУЛЬСОВ
Складывая ломанные, получаем - Количество движения - это вектор, равный геометрической сумме количества движения отдельных точек системы. Если тело или система вращаются, то для любой пары точек при вращении тела количество движения
Рассматривая К-ую точку системы с учетом действия внешних и внутренних сил:
суммируя по точкам системы, соответственно получим
Формула (1) выражает теорему о количество движения системы «К» в дифференциальной форме. Векторная производная от количества движения системы по времени равно главному вектору внешних сил
СЛЕДСТВИЕ: Закон сохранения количества движения системы: 1) Если главный вектор внешних сил равен нулю, т.е. внешние силы взаимноуравновешиваются ((
2) Если гл.вектор не равен 0, (
Изменение количества движения системы за определенный промежуток времени равен импульсу равнодействующей внешних сил.
В координатной форме(например на ось Х):
ПРИМЕРЫ: Дано Vo=0 m1…mn


В момент t, за счет электродвигателя создается угловая скорость ω2, которая создает скорости V4 и V3 V4= V2- ω2 V3=R2∙ ω2 где V1скорость реагирования корпуса веса
На основании (1) Кхнач=0, то 0=
 Если Если 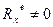 здесь здесь  , , 
если расход воды, где F - теорема в проекции на ось Х:
Теорема моментов До сих пор мы вычисляли момент силы относительно некоторого неподвижного центра О.
где Аналогично вычислим момент количества движения точки относительно неподвижного центра О:
Установим зависимость кинетического момента точки и момента силы F, действующей на нее. Для чего продифференцируем
Векторная производная от кинетического момента точки по времени равна моменту силы, действующей на нее относительно той же неподвижной точки О. Если момент силы равен нулю, то кинетический момент остается постоянным, что выражает закон сохранения кинетического момента:
Груз веса Р двигается по окружности радиуса Найти
При изменении КИНЕТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ
Рассмотрим систему материальной точки и выберем точку Мk массой mк,скорость которой Vk, на нее действуют внешние и внутренние силы ; ↓ ↓
Тогда:
Следствие: закон сохранения кинетического момента системы: если
Кинетический момент твердого тела при вращении вокруг неподвижной оси Вычислим Для всего тела: Здесь Следовательно
Для демонстрации закона сохранения кинетического момента системы представлена платформа Жуковского: ℓ→R

Дано: Найти: при переходе точки на край диска
I.
↓ ↓
Т. к..
II. Если Если
Здесь: 2)
↓ ↓
3)

Примеры вычисления работы силы
1. Работа силы тяжести. Р-вес тела. Здесь Х=0, Y=0, Z=-P dA=Zdz
Работа силы тяжести не зависит от формы траектории перемещения точки. В таких случаях сила действующая на точку называется потенциальная.
2. Работа упругой силы.
dA=-cxdx
т. к. ch=Pmax.
Здесь перемещение может происходить по различным траекториям. Работа же не зависит от формы перемещения точки, упругая сила Р– тоже потенциальная сила. 3.
Работа зависит от dS, т.е сила Fтр не потенциальная.
4.Работа момента силы.

Мощность силы
Мощность силы – величина,определяющая работу силы, совершенную в единице времени.
Т.к как в настоящее время используются две системы единиц: СИ и техническая система единиц, то в технической системе ед. А в системе СИ:
Теорема Кенига Рассмотрим общий случай движения твердого тела по отношению к неподвижной системы координат. Положим, что тело в своём относительном движении совершает поворот вокруг мгновенной оси РС с мгновенной угловой скоростью ω. «С» имеет скорость

Тогда кинетическая энергия тела: Т=
тогда: Т=
Здесь
Частные случаи
1. Поступательное движение точек тела 2. Вращательное движение тела вокруг неподвижной оси:
Плоско параллельное движение твердого тела
Примеры вычисления кинетической энергии системы

Дано: ω, OА,
р Расмотрим движение точки массой m под действием силы
Установим зависимость между работой силы и кинетической энергией:
dS – элементарное перемещение вдоль касательной.
Уравнение (1) выражает теорему об изменении кинетической энергии. Таким образом, изменение кинетической энергии материальной точки при некотором ее перемещении равно работе, действующей на нее силы на том же перемещении, т.е. за счет изменения кинетической энергии совершается работа. Рассмотрим систему n точек M1 … Mn и рассмотрим Mk -точку, к которой приложены внешние и внутренние силы, тогда суммируя по n точкам системы, получим
Т.К работа внутренних сил равна нулю (
Изменение кинетической энергии системы при некотором ее перемещении равна сумме работ всех внешних сил, действующих на систему на том же перемещении. Частные случаи 1.Поступательное движение твердого тела Система сил инерции точек приводится к главному вектору сил инерции: где ас Если радиус-вектор i -ой точки умножить на равенство (1), то получим:
Т.е. геометрическая сумма главных вектор-моментов заданных сил, реакций связи и вектор –момента от силы инерции в любой момент времени равна нулю.
 т.е т.е
т.е. направление главного момента от сил инерции противоположно направлению углового ускорения Таким образом, при вращении тела вокруг оси силы инерции точек тела приводится только к главному моменту сил инерции относительно оси:
3. Плоско-параллельное движение Тело двигается в плоскости симметрии xoy. Ускорене центра масс В данном случае система сил инерции точек тела приводится к главному вектору сил инерции и к главному моменту от сил инерции относительно
  ; ; 
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
Обобщенные координаты Число степеней свободы Перемещение системы и отдельных ее точек не может происходить произвольно. Их перемещение ограничено определенными условиями - связями. В динамике связи будем классифицировать по ряду признаков: 1. Стационарная и нестационарная связь Стационарная связь - это связь, уравнение которой не содержит времени.
u - скорость троса
Эта связь нестационарная т.к ее уравнение входит время t:
3. Стационарная, двухсторонняя удерживающая
4. Связь, не накладывающая ограничения на скорость тела, называется голономной связью. Связь, накладывающая ограничения на скорость называется неголономной связью. В аналитической механике применяется принцип освобождаемости от связей и тогда отдельные точки являются свободными и к ним приложены все заданные силы и реакции связей. Отдельные точки системы могут совершать определенные перемещения, допускаемые связями. Возможными или виртуальными перемещениями точек системы называют воображаемые, бесконечно малые перемещения точек, которые допускают связи, наложенные на систему в данный момент. Например:
  - прямолинейные в виду их малости - прямолинейные в виду их малости
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.241 (0.291 с.) |



 откуда:
откуда: 

 , т.е.:
, т.е.: 



 = ∑X;
= ∑X;  = ∑Y
= ∑Y сos kt; - m r k
сos kt; - m r k  cos t =∑X;
cos t =∑X; 

 sin kt; - m r k
sin kt; - m r k 
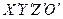 - не равномерное вращение
- не равномерное вращение
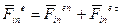


 т.е. справедливо равенство (3)
т.е. справедливо равенство (3)









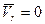 ,
,  ,
,  ,
,  , то
, то  , тогда уравнение (3) примет вид:
, тогда уравнение (3) примет вид:
 ), динамической реакции связи (равнодействующая
), динамической реакции связи (равнодействующая  ) и переносной силы инерции (
) и переносной силы инерции ( ), геометрическая сумма которых равна нулю, и выражает принцип Даламбера для несвободной материальной точки.
), геометрическая сумма которых равна нулю, и выражает принцип Даламбера для несвободной материальной точки. , получим N=0, т. е. состояние невесомости
, получим N=0, т. е. состояние невесомости - количество движения.
- количество движения. (Нсек)
(Нсек)
 - мера действия силы - работа A= Р∙Х (Нм)
- мера действия силы - работа A= Р∙Х (Нм) - Равнодействующая внешних сил.
- Равнодействующая внешних сил.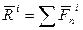 - Равнодействующая внутренних сил.
- Равнодействующая внутренних сил.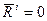

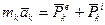 К=1……n
К=1……n
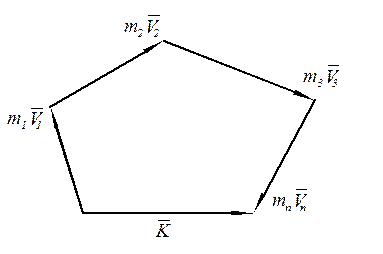
 .
. =0 и
=0 и будет определять только поступательное движение.
будет определять только поступательное движение.
 (1)
(1)
 , то количество движения системы постоянная величина,
, то количество движения системы постоянная величина, 
 . Тогда
. Тогда 


 (2) т.е.
(2) т.е. (3) если Xе=0, то проекция кол-ва движения
(3) если Xе=0, то проекция кол-ва движения 


 (1)
(1)

 отсюда находим
отсюда находим 


 т. к..
т. к.. 
 , тогда:
, тогда:  , откуда
, откуда 

 (1)
(1) - радиус, вектор точки, проведенный из неподвижного центра О.
- радиус, вектор точки, проведенный из неподвижного центра О. - выражает кинетический момент точки и аналогично моменту
- выражает кинетический момент точки и аналогично моменту  запишем:
запишем: 



 по t:
по t: по:
по: 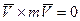 т.к. (
т.к. ( )
) , следовательно:
, следовательно: (3)
(3)
 т.е.
т.е.  . В координатной форме:
. В координатной форме: 


 со скоростью
со скоростью  , а затем на расстоянии
, а затем на расстоянии  от Z
от Z и
и 
 , т. к.
, т. к.  , то
, то  . Т. е.
. Т. е. 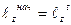 или
или через
через 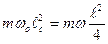

 и
и  . Тогда для системы и точек:
. Тогда для системы и точек: =
=  К=1…….n
К=1…….n кин.мом.сист.
кин.мом.сист.  -главный момент внешних сил
-главный момент внешних сил -главный момент внутренних сил равен 0
-главный момент внутренних сил равен 0 (7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра.
(7). Тогда формула (4) выражает теорему о изменении кинетического момента системы в дифференциальной форме: векторная производная от момента количества движения системы по времени относительно центра 0 равна главному моменту внешних сил относительно такого же центра. (4) в координатной форме:
(4) в координатной форме: 

 (главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная.
(главный момент внешних сил относительно неподвижного центра = О), то и кинетический момент системы есть величина постоянная. т.е.
т.е.  (5)
(5) для точки массой m:
для точки массой m: 

 -момент инерции тела.
-момент инерции тела.
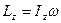 кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость.
кинетический момент твердого тела относительно оси равен произведению моменту инерции тела на угловую скорость. 

 т.е.
т.е. 
 =
= 



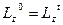 , то:
, то:  ,
, 
 не равен 0:
не равен 0: пусть
пусть 
 интегрируя:
интегрируя:
 (2) В момент t сек точка массой
(2) В момент t сек точка массой  переходит в положение В, имея при этом относительную скорость
переходит в положение В, имея при этом относительную скорость  , тогда
, тогда

 (3), где
(3), где  т. к.
т. к.  получаем
получаем  (Нм)
(Нм)
 где «с» коэффициент жесткости пружины
где «с» коэффициент жесткости пружины Эл. работа:
Эл. работа: 
 (здесь
(здесь  )
)

 но
но 
 или
или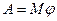 при F=const
при F=const Ватт=дж.сек. (1)
Ватт=дж.сек. (1) где 1л\с= 75кГс.м
где 1л\с= 75кГс.м (где
(где  -кГсм,
-кГсм, 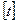 - сек)
- сек)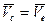



 скорости
скорости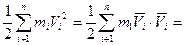
 )=
)=
 (1)
(1)
 так как во вращении вокруг оси РС выражение
так как во вращении вокруг оси РС выражение  для любой пары точек, как указывалось в теореме о количества движения системы, т. е. кинетическая энергия твердого тела при любом его движении равна сумме кинетической энергии центра масс,в котором сосредотачивается вся масса системы(М), и кинетическая энергия тела в его относительном движении по отношению к центру масс.
для любой пары точек, как указывалось в теореме о количества движения системы, т. е. кинетическая энергия твердого тела при любом его движении равна сумме кинетической энергии центра масс,в котором сосредотачивается вся масса системы(М), и кинетическая энергия тела в его относительном движении по отношению к центру масс. 

 , где
, где - момент инерции тела относительно оси СР
- момент инерции тела относительно оси СР
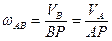



 Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы






 (1)
(1)
 ), то выражение теорема об изменении кинетической энергии будет иметь вид:
), то выражение теорема об изменении кинетической энергии будет иметь вид:
 ,
, - сумма масс всех точек;
- сумма масс всех точек;
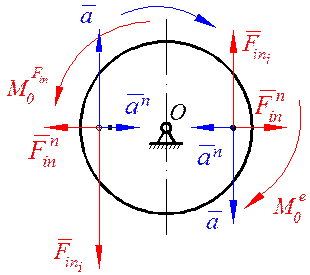 Касательное ускорение
Касательное ускорение  обеспечивается
обеспечивается  (моментом внешних сил), который равен:
(моментом внешних сил), который равен:

 .
.
 и угловое ускорение
и угловое ускорение 
 В противном случае связь нестационарная. Например крльцо А:
В противном случае связь нестационарная. Например крльцо А: текущая длина троса
текущая длина троса
 - уравнение связи
- уравнение связи

 2. Стационарная, односторонняя неудерживающая
2. Стационарная, односторонняя неудерживающая
 и
и 



