
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения плоского движения твердого телаСодержание книги
Поиск на нашем сайте
Учитывая, что плоское движение есть совокупность поступательного движения вместе с полюсом «С» и вращается вокруг «С», а уравнения плоского движения:
дифференциальные уравнения плоского движения твердого тела:
 
РАБОТА СИЛЫ НА КОНЕЧНОМ ПУТИ Для характеристики действия силы на тело при некотором его перемещении вводится понятие работы силы (скалярная величина). При этом работу совершает та сила, которая может изменить модуль скорости, но не направление.
Fτ=Fsinα-может изменить модуль скорости
Элементарная работа: dA=Fτ dS(1) где Если движение описать в векторной форме, то В координатной форме Fx FyFz -проекция сил; где Тогда работа силы F на участке
Примеры вычисления работы силы
1. Работа силы тяжести. Р-вес тела. Здесь Х=0, Y=0, Z=-P dA=Zdz
Работа силы тяжести не зависит от формы траектории перемещения точки. В таких случаях сила действующая на точку называется потенциальная.
2. Работа упругой силы.
dA=-cxdx
т. к. ch=Pmax.
Здесь перемещение может происходить по различным траекториям. Работа же не зависит от формы перемещения точки, упругая сила Р– тоже потенциальная сила. 3.
Работа зависит от dS, т.е сила Fтр не потенциальная.
4.Работа момента силы.

Мощность силы
Мощность силы – величина,определяющая работу силы, совершенную в единице времени.
Т.к как в настоящее время используются две системы единиц: СИ и техническая система единиц, то в технической системе ед. А в системе СИ:
Вычисление кинетической энергии тела в общем случае его движения Теорема Кенига Рассмотрим общий случай движения твердого тела по отношению к неподвижной системы координат. Положим, что тело в своём относительном движении совершает поворот вокруг мгновенной оси РС с мгновенной угловой скоростью ω. «С» имеет скорость

Тогда кинетическая энергия тела: Т=
тогда: Т=
Здесь
Частные случаи
1. Поступательное движение точек тела 2. Вращательное движение тела вокруг неподвижной оси:
Плоско параллельное движение твердого тела
Примеры вычисления кинетической энергии системы

Дано: ω, OА,
р Расмотрим движение точки массой m под действием силы
Установим зависимость между работой силы и кинетической энергией:
dS – элементарное перемещение вдоль касательной.
Уравнение (1) выражает теорему об изменении кинетической энергии. Таким образом, изменение кинетической энергии материальной точки при некотором ее перемещении равно работе, действующей на нее силы на том же перемещении, т.е. за счет изменения кинетической энергии совершается работа. Рассмотрим систему n точек M1 … Mn и рассмотрим Mk -точку, к которой приложены внешние и внутренние силы, тогда суммируя по n точкам системы, получим
Т.К работа внутренних сил равна нулю (
Изменение кинетической энергии системы при некотором ее перемещении равна сумме работ всех внешних сил, действующих на систему на том же перемещении.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.236 (0.006 с.) |


 φ= φ(t) то:
φ= φ(t) то:
 φ =
φ = 

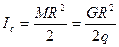
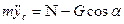



 меняет направление скорости но не модуль поэтому работы не совершает.
меняет направление скорости но не модуль поэтому работы не совершает.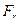 проекция силы на направление- перемещения.
проекция силы на направление- перемещения. (2)
(2) (3)
(3) -приращение радиуса-вектора точки приложения
-приращение радиуса-вектора точки приложения 
 :
: 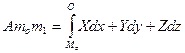 (4)
(4) (Нм)
(Нм)
 где «с» коэффициент жесткости пружины
где «с» коэффициент жесткости пружины Эл. работа:
Эл. работа: 
 (здесь
(здесь  )
)

 но
но 
 или
или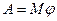 при F=const
при F=const Ватт=дж.сек. (1)
Ватт=дж.сек. (1) где 1л\с= 75кГс.м
где 1л\с= 75кГс.м (где
(где  -кГсм,
-кГсм, 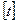 - сек)
- сек)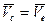



 скорости
скорости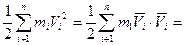
 )=
)=
 (1)
(1)
 так как во вращении вокруг оси РС выражение
так как во вращении вокруг оси РС выражение  для любой пары точек, как указывалось в теореме о количества движения системы, т. е. кинетическая энергия твердого тела при любом его движении равна сумме кинетической энергии центра масс,в котором сосредотачивается вся масса системы(М), и кинетическая энергия тела в его относительном движении по отношению к центру масс.
для любой пары точек, как указывалось в теореме о количества движения системы, т. е. кинетическая энергия твердого тела при любом его движении равна сумме кинетической энергии центра масс,в котором сосредотачивается вся масса системы(М), и кинетическая энергия тела в его относительном движении по отношению к центру масс. 

 , где
, где - момент инерции тела относительно оси СР
- момент инерции тела относительно оси СР
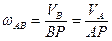



 Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы






 (1)
(1)
 ), то выражение теорема об изменении кинетической энергии будет иметь вид:
), то выражение теорема об изменении кинетической энергии будет иметь вид:



