Definition of the optimum sequence of calculation of CTS.

The problem of definition of the optimum sequence of calculation of CTS finishes the analysis of structure of CTS and is carried out in two stages. At the first stage make the analysis of structure of CTS in general with allocation of the CTS complexes and definition of a preliminary procedure of payments of CTS, and also define all contours entering the allocated complexes. At the second stage make the analysis of structure of complexes, define communications which rupture allows to translate complexes to the opened look, and define the final sequence of calculation of CTS.

There is a set of various algorithms of allocation of complexes which are connected with option of formalization of CTS. Usually, these algorithms are connected with matrix operations, and with further transformation of the turned-out matrixes by means of logical operations. These methods are rather well developed and in detail presented in literature. Because the expert who is carrying out the analysis of structure of CTS usually automatically uses already ready developments, these methods aren't given in the present abstract of lectures.

Unlike methods of allocation of complexes, algorithms of search of an optimum set of the broken links of a complex, have no unambiguous decision since the structure of the count doesn't contain information on features of his communications.

The concept of parametricity of communication (stream), i.e. the number of parameters, characterizing a stream in concrete consideration, is generalizing, and is connected both with properties of a stream, and with an algorithm of calculation of modules from where the interesting communication comes out and where it is directed. By search of an optimum set of the broken links it is necessary to consider the rule: total parametricity of the broken links of a complex has to be minimum. We will consider a concept of parametricity on an example.

As an example, we will consider the scheme of the movement of material streams in a radiant part of a copper with natural circulation (Fig. 4.7).

Fig. 4.7. Process flow diagram of a copper

 

According to the technological scheme, feed water from a drum of a copper (4) on lowering pipes (1) is pumped in a collector (2), and then distributed on vaporizing pipes (3). The steam phase formed in vaporizing pipes at the expense of a difference of density rises together with liquid up, in a drum. In a copper drum dry saturated steam is separated from liquid and moves to the consumer. The consumption of steam is compensated by giving of feed water so that level in a drum of a copper remained fixed. The operator scheme and the count of the specified technological scheme are provided in Fig. 4.8.

Fig. 4.8. Operator scheme (a) and count of the scheme (b) of a copper

 

The count provided in the drawing has one complex including the flows 1, 2 and 3 entering one contour. Before determining the number of parameters, which it is possible, to characterize a condition of the flows entering a complex we will consider a phase condition of flows: 1 – Liquid, 2 – Steam + Liquid, 3 – Liquid. To characterize a condition of the liquid flows (1 and 3) consisting of water it is necessary to know them: general expense and temperature. To characterize parameters of a vapor-liquid flow (2), it is necessary to know: general expense, temperature and share of a steam phase (dryness degree). Besides, as in system there is a reel, i.e. the module where vapor-liquid balance is reached, it is necessary to know pressure of each flow. However it is possible to assume that in a copper (i.e. for all flows) there is an isobaric process therefore pressure can be excluded from parameters of flows.

Thus, parametricity of flows (the number of the parameters characterizing in this consideration) will be following:

 

Flow	Parametricity

According to the rule of the choice of the broken-off flows "total parametricity of the broken links of a complex shall be is minimum" it is possible to conclude that for the translation of a complex from closed in the opened condition, it is possible to break off a flow 1 or 3.

In case of a gap of a flow 1, flows will be flows, entrance in this CTS: 5 and 1', and days off: 4 and 1, and, in case of achievement of the decision, the expense and temperature of flows 1 and 1' shall be identical. For a possibility of calculation of CTS, to the place of a gap the IB iterative block (see Fig. 4.9) which main objectives will be will be established: total determination of an error in the parameters (an expense and temperature) of flows changing in settlement process 1 and 1', and determination of parameters of a flow 1' in case of the known parameters of a flow 1 according to the chosen mathematical method of convergence.

Fig. 4.9. The operator scheme with the iterative block

 

As parametricity characterizes the number of parameters which can change, the solution of CTS by a decompositional method will happen until the total size of an error (Err), taking into account the set weight coefficients (wG, wT, etc.), isn't less or is equal to the set accuracy of calculation (Eps):

[4.1]

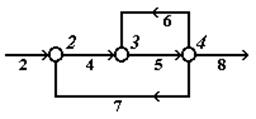
Sizes of weight coefficients usually are chosen so that to balance a contribution of parameter values, various on absolute value, to a mistake.

It should be noted that in case of a gap of the flow 2 having big parametricity, the accuracy of calculation of a complex will need to be calculated not in two parameters (G and T), and on three (G, T and X) what much more difficult will also involve big costs for achievement of the decision. Besides, it is necessary to consider that there are always mathematical problems of convergence of calculation of systems regardless of a method of their calculation.

When calculating more difficult CTS cases when the complex has more than one contour rather often meet, and one of flows is general (see Fig. 4.10).

Fig. 4.10. An illustration of the complex having two circuits

 

For a rupture of a circuit 2-3-4-2 (on peaks), depending on parametricity of flows, it is possible to break off any of flows: 4, 5 or 7. For a rupture of a circuit 3-4-3 (on peaks), depending on parametricity of flows, it is possible to break off a flow 5 or 6. Thus, the flow 5 is the general, therefore, in case of its gap both circuits at the same time will be broken off. At the same time it is possible to claim that parametricity of one flow will always be less summary parametricity of two flows which would need to be broken off in case of a rupture of two circuits. In case of more complex structure of a complex (three and more circuits of a complex have one general flow), the last statement won't raise doubts any more.

Thus, it is possible to formulate the following translation rules of a complex from a closed look to opened (a rupture of flows):

1. In a complex the set of the flows having the smallest summary parametricity is always broken off;

2. If in a complex there are flows which are at the same time entering several circuits of a complex, then these flows can be broken off without additional analysis of value of their parametricity.

After determination of an optimum set of the broken-off circuits which summary parametricity is minimum there is an opportunity to define the final sequence of calculation of all CTS taking into account the broken-off flows, i.e. taking into account the flows quitting iterative units which for CTS translated from shorted to an open-ended look also will be input. Further, the final sequence of calculation of CTS is transmitted to the coordinating software which allows to make of modules of the database to make CTS of the given look and to make its calculation.

Test questions

1. Describe tasks of the analysis of structures of CTS.

2. What methods of representation of CTS exist.

3. Graph theory elements.

4. Explain an essence of the task of determination of the optimum sequence of calculation of CTS.