
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мал.7.1. Геометричний метод рішення задачі лінійного
Програмування Відповідь: виробів моделі А – 300 од. виробів моделі В – 200 од. максимальний прибуток
Симплексний метод рішення. Нехай потрібно мінімізувати цільову функцію при обмеженнях (7.4). Приведемо (7.4) до стандартного виду (7.2). Для цього до лівої частини кожного обмеження, що має вид нерівності ≤, добавляємо позитивну змінну:
Усього перемінних Th. Нехай область припустимих рішень - обмежений замкнутий багатогранник, тоді мінімальне (максимальне) значення функції мети досягається в кутовій точці. Оскільки число невідомих Виз. Рішення називається базисним, якщо вільні перемінні рівні нулю. Кожне базисне рішення відповідає кутовій точці. Кількість базисних рішень: Таким чином, щоб знайти оптимальне рішення, потрібно обчислити значення функції мети у всіх кутових точках і вибрати точку, у якій значення функції мети мінімально (максимально); якщо Виз. Симплексний метод - упорядкований перехід від одного базисного рішення до іншого, при якому відбувається зменшення значення функції мети. (Використовується для відшукання мінімального значення функції мети) Розглянемо побудову нульового базисного рішення. Припустимо, що система обмежень (7.3) містить
Базисні перемінні:
Далі виникає необхідність перевірити, чи не є знайдене базисне рішення оптимальним. Помітимо, що вектори
Вектори
Оскільки базис одиничний, те Th: (критерій оптимальності) Якщо для деякого базисного рішення
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.234.191 (0.007 с.) |

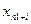 . Якщо обмеження у виді нерівності ≥, те з лівої частини віднімаємо
. Якщо обмеження у виді нерівності ≥, те з лівої частини віднімаємо 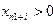 . Система прийме вид:
. Система прийме вид: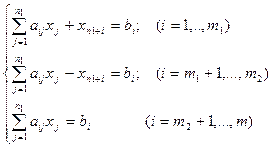
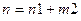 . Усі
. Усі  повинні бути позитивні, якщо
повинні бути позитивні, якщо  , те дане рівняння потрібно помножити на (-1). Оскільки цільова функція не має стаціонарних точок, те своїх максимального і мінімального значень вона досягає на границі області.
, те дане рівняння потрібно помножити на (-1). Оскільки цільова функція не має стаціонарних точок, те своїх максимального і мінімального значень вона досягає на границі області. більше числа рівнянь
більше числа рівнянь  , те частина невідомих покладається базисними. Вільні перемінні переносяться в праву частину. Система зважується щодо базисних перемінних. Така система має рішення, якщо визначник, що складається з коефіцієнтів при базисних невідомих у системі обмежень відмінний від чи нуля якщо вектори
, те частина невідомих покладається базисними. Вільні перемінні переносяться в праву частину. Система зважується щодо базисних перемінних. Така система має рішення, якщо визначник, що складається з коефіцієнтів при базисних невідомих у системі обмежень відмінний від чи нуля якщо вектори  , відповідні базисним перемінної, є незалежними.
, відповідні базисним перемінної, є незалежними.

 ; інші
; інші 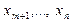 - вільні. Нехай вільні змінні рівні нулю, тоді отримуємо нульове базисне рішення:
- вільні. Нехай вільні змінні рівні нулю, тоді отримуємо нульове базисне рішення: .
.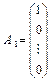 ;
;  ;…;
;…;  ;
; 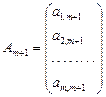 ;…;
;…; 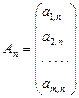 .
. ,…,
,…,  – одиничні й утворять базис у
– одиничні й утворять базис у 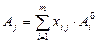
 . Кожному розкладанню
. Кожному розкладанню  :
: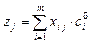
 розкладання усіх векторів
розкладання усіх векторів 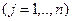 задовольняють умові
задовольняють умові 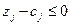 , то план
, то план 


