
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 7. Рішення задач лінійного
ПРОГРАМУВАННЯ.
План лекції 1. Постановка задачі. 2. Геометричний метод рішення. 3. Симплексний метод рішення. Постановка задачі. Лінійне програмування - наука, що вивчає методи перебування мінімального і максимального значень лінійної функції, на невідомі який накладені лінійні обмеження. Розглянемо лінійну функцію: Така функція називається цільовою функцією. Нехай на невідомі функції накладені обмеження:
Потрібно знайти такий набір значень невідомих Виз. Безліч значень X, що задовольняє системі обмежень (7.2), називається областю припустимих рішень. Рішення з цієї області називається планом. У векторному виді задача лінійного програмування виглядає в такий спосіб. Нехай треба мінімізувати (максимізувати) лінійну форму:
Виз. План називається опорним, якщо серед векторів
Виз. Оптимальним називається план, що задовольняє системі (7.2) і мінімізує (максимізує) функцію мети. У реальних задачах система обмежень може містити нерівності. Тоді система обмежень має вид:
Геометрично перші
Геометричний метод рішення. Цей метод використовується у випадку двох перемінних:
з граничною прямою
Приклад7.1. Фірма робить 2 моделі книжкових полиць. Виробництво обмежене наявністю сировини і часом машинної обробки. Для кожного виробу моделі А потрібно Фірма робить 2 моделі книжкових полиць. Виробництво обмежене наявністю сировини і часом машинної обробки. Для кожного виробу моделі А потрібно 3 м2 дощок, для В – 4 м2. Фірма одержує до 1700 м2 дощок у тиждень. Для кожного виробу А потрібно 12 хвилин машинного часу, для В - 30 хвилин. У тиждень можна використовувати не більш 160 годин. Скільки виробів кожної моделі треба зробити за тиждень, щоб одержати максимальний прибуток, якщо одиниця виробу типу А дає прибуток - Рішення.
Функція мети - прибуток при реалізації усіх виробів.
2 обмеження: 1- на використання матеріалів (дощок) 2- на час машинної обробки
Кожне обмеження геометрично є напівплощиною. Граничні лінії:
Побудуємо на графіку область допустимих рішень. Областю припустимих рішень є чотирикутник Градієнт функції мети: Будуємо лінію з нульовим рівнем: Пересуваючи нульову лінію рівня таким чином, щоб вона перетиналася з областю припустимих рішень, одержимо, що крайній є точка С - це точка максимуму. Знайдемо її координати, вирішуючи систему:
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.28.179 (0.006 с.) |
 (7.1)
(7.1)

 , який задовольняв би системі (7.2) і мінімізував (максимізував) функцію мети.
, який задовольняв би системі (7.2) і мінімізував (максимізував) функцію мети. при обмеженнях:
при обмеженнях:  ; де
; де  ,
, 
 ,…,
,…, 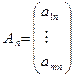 ,
,  (7.3)
(7.3)

 векторів лінійно незалежні.
векторів лінійно незалежні.
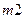 обмеження являють собою на півплощини.
обмеження являють собою на півплощини. и
и  (на площині). Нехай потрібно мінімізувати (максимізувати) лінійну функцію:
(на площині). Нехай потрібно мінімізувати (максимізувати) лінійну функцію:  при обмеженнях:
при обмеженнях:

 . Обмеження, що залишилися - прямі. Областю припустимих рішень є їхнє перетинання. Область припустимих рішень може являти собою замкнутий чи відкритий багатокутник, промінь, крапку і т.д. Нехай безліч припустимих рішень - обмежений замкнутий багатокутник. Лініями рівня цільової функції є набір рівнобіжних прямих. Значення функції зростає в напрямку градієнта, убуває в напрямку антиградієнта. Будуємо лінію з нульовим рівнем:
. Обмеження, що залишилися - прямі. Областю припустимих рішень є їхнє перетинання. Область припустимих рішень може являти собою замкнутий чи відкритий багатокутник, промінь, крапку і т.д. Нехай безліч припустимих рішень - обмежений замкнутий багатокутник. Лініями рівня цільової функції є набір рівнобіжних прямих. Значення функції зростає в напрямку градієнта, убуває в напрямку антиградієнта. Будуємо лінію з нульовим рівнем:  . У випадку мінімізації функції мети будемо пересувати цю лінію паралельно самої собі в напрямку антиградієнта таким чином, щоб вона перетиналася з областю припустимих рішень. Тоді крайнє положення, що займе ця лінія визначає точку мінімуму. При рішенні задачі максимізації нульову лінію рівня треба переміщати в напрямку градієнта.
. У випадку мінімізації функції мети будемо пересувати цю лінію паралельно самої собі в напрямку антиградієнта таким чином, щоб вона перетиналася з областю припустимих рішень. Тоді крайнє положення, що займе ця лінія визначає точку мінімуму. При рішенні задачі максимізації нульову лінію рівня треба переміщати в напрямку градієнта. ; одиниця виробу типу В-
; одиниця виробу типу В-  .
.

 ,
, 

 .
.
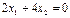 ;
; 

 максимальний прибуток
максимальний прибуток



