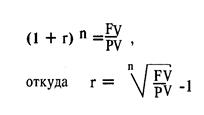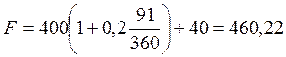Расчет годовых ставок процента

Очевидно, что при одинаковых условиях (одинаковый срок, простой или сложный процент) выгоднее та инвестиция, у которой выше процентная ставка. Однако зачастую сроки инвестиций и периоды выплат по ним не совпадают. В этом случае для того, чтобы сравнивать инвестиции, необходимо рассчитывать их процентные ставки, приведенные к одному и тому же временному периоду. Как правило, в качестве такого периода выбирается год.

Пример. Вклад в банке дает 1% за 14 дней. Найти годовую ставку процента.

Годовая ставка процента

В общем случае она вычисляется из формулы простого процента:

Если мы используем формулу сложного процента, то на единицу вложений годовая процентная ставка составит (1 + процентная ставка в периоде начисления в долях единицы), возведенная в степень, равную числу периодов начисления, минус единица:

(1 + r) ⁿ - 1.

Пример. По банковскому вкладу ежеквартально начисляют доход 2% от первоначальной суммы вклада. Найти ставку процента (в годовых) с учетом реинвестирования полученного дохода.

(1 + 0,02)⁴ - 1 = 1,082432 - 1 = 0,0824.

При прочих равных условиях инвестирования годовая процентная ставка с учетом реинвестирования выше.

В общем случае вычисляется:

С учетом необходимости приведения процентных ставок к одному временному периоду их общие формулы расчета видоизменяются в зависимости от того, в каких единицах (днях, месяцах, кварталах) выражен период инвестирования.

Например, если инвестиция имеет срок, выраженный в днях, то число периодов п =-365/х, где х — число дней, то процентная ставка равна:

Процентная ставка равна:

Будучи рассчитана на основе одного временного периода (т. е. n = 1), формула приобретает совсем простой вид:

Внутренняя ставка доходности

Иногда требуется решить обратную задачу: при какой процентной ставке по данному вложению текущая стоимость вложения будет равна ее рыночной стоимости? Для ответа на этот вопрос нужно решить уравнение (8) относительно г. Такое значение r называется внутренней (ибо не зависит от внешних условий) ставкой доходности. Считается, что инвестиция тем выгоднее, чем выше ее внутренняя ставка доходности.

Пример.

Облигация сроком 1 год погашается по номиналу, выплачивается ежегодный купонный доход 8% номинала. Рыночная цена облигации — 98,18 номинала. Найти внутреннюю ставку доходности.

Пусть номинал — 100, тогда

С = 100 х 0,08 = 8, FV = 100, PV=98,18,

a r предстоит найти. Подставляя полученные значения в формулу, получаем:

Отсюда:

1 + r = 108/98,18- 1,10,

и наконец, внутренняя ставка доходности равна: r - 0,1 = 10%.

Пример. Найти внутреннюю ставку доходности для вложения 9 500 руб. на банковский вклад сроком на 3 года с выплатой 10% годовых без реинвестирования процентного дохода.

Если мы найдем внутреннюю ставку доходности для облигации по условиям Примера 7, то, решив уравнение

мы можем убедиться, что внутренняя норма прибыли для вложений в облигацию чуть выше, значит, они выгоднее, что соответствует выводам, сделанным ранее.