
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Основы финансовых вычисленийСодержание книги
Поиск на нашем сайте
Два способа расчета процентных выплат (простой процент, сложный процент). Изменение стоимости денег во времени. Расчет годовых ставок процента. Понятие о дисконтировании денежных потоков. Внутренняя ставка доходности. Аннуитеты.
Давая деньги в долг, кредитор упускает возможность использовать их до момента возврата. Заемщик должен выплатить компенсацию за ожидание кредитора. Компенсация обычно выражается в форме процента.. Процентом называют доход в денежной форме, выплачиваемый кредитору за пользование его деньгами. Процент начисляется на основную сумму вклада (займа) по определенной процентной ставке с определенной периодичностью, например ежегодно. Существует несколько основных показателей, необходимых для расчета и по которым можно классифицировать проценты. Важнейшим показателем при расчете процентов является база начисления – это первоначальная сумма активов, на которую производится начисление процентов или, соответственно, с которой сопоставляется полученная прибыль при вычислении доходности. Метод начисления – это способ, по которому рассчитывается конечная сумма активов. По методу начисления проценты можно разделить на: – простые; – сложные; – смешанные. Критерием разделения метода начисления процентов выступает база начисления. При простых процентах база начисления остается неизменной на всем протяжении срока начисления, т.е. проценты начисляются на ту сумму активов, которая была в начальный момент времени: Критерием разделения метода начисления процентов выступает база начисления. При простых процентах база начисления остается неизменной на ту сумму активов, которая была в начальный момент времени:
где FV – сумма активов в конечный период; PV – сумма активов в конечный период; r – ставка процента. В случае начисления сложный процентов база начисления возрастает каждый раз, когда к основной сумме долга добавляются проценты, начисленные в предыдущем периоде. Такой процесс называется капитализацией процентов. В результате темп прироста конечной суммы активов при начислении по сложной ставке. Формула расчета конечной стоимости активов по сложной ставке процентов имеет следующий вид:
где n – число периодов начисления процентов.
При начислении процентов по сложной ставке возникают трудности с дробным числом периодов начисления. Например, при начислении процентов в течение 3,5 лет. В таком случае принято применять смешанный метод начисления, при котором сложные проценты начисляются на целое число периодов (в рассматриваемом случае 3 года), а начисление дробной части ведется по простой ставке процента:
где – n – целая часть периода начисления; k – дробная часть периода начисления.
Другим важным показателем, используемым при расчете процентов, является временной интервал, или период начисления процента, – промежуток времени, на протяжении которого происходит начисления процентов. Существует три основные системы расчета временного интервала: – немецкая; – англо-американская; – французская. Между собой они различаются по правилам расчета срока вложений и количеству дней в году. Самая точная – англо-американская система не позволяет делать никаких округлений при расчете периода начислений процентов. В результате по этой системе количество дней в году соответствует его реальному значению: 365 или 366, а период начисления рассчитывается исходя из календарного количества дней в каждом месяце: 28, 29, 30, 31. В менее строгой французской системе учета временного интервала количество дней в году принимается равным 360, а расчет периода начисления производится исходя из календарного количества, как и в американской системе. Немецкая же система расчета временного интервала может считаться самой терпимый к округлениям, так как она предполагает, что в году 360 дней, а каждом месяце их по 30. Пример: Депозит в сумме 1 000 000 руб. был размещен в банке под 80% годовых 11.03.01 и востребован 15.08.01. Необходимо определить сумму депозита, которая была получена. При немецкой системе учета и начисления процентов период начисления определяется: d = 19+30+30+30+30+15 = 154 дня. Тогда сумма депозита равна:
По французской системе получаем: d = 20+30+31+30+31+15 = 157 дня,
Соответственно, по английской системе: d = 20+30+31+30+31+15 = 157 дня,
Таким образом, для инвестора выгоднее начисление процентов с расчетом временного интервала по французской системе, тогда как банку выгоднее немецкая система расчета. Любые сколь угодно сложные финансовые вычисления базируются на двух концептуальных методах расчета: – метода наращивания; – метода дисконтирования. Метод наращения используется для вычисления суммы активов, которая будет получена через определенное время, если на нее будут начисляться проценты по действующей ставке, которая, в свою очередь, называется ставкой (r). Ее можно определить по формуле:
где FV – будущая стоимость активов; PV – современная стоимость активов. Метод дисконтирования по своей сути противоположен методу наращения и используется для определения суммы, которую необходимо уплатить сейчас при заданном уровне доходности операции, для того чтобы получить доход в будущем. Ставка процента, используемая в данном случае, называется ставкой дисконтирования, которая определяется по формуле:
Для описания финансовых расчетов будем применять обозначения, которые использовались ранее, в частности: r – годовая процентная ставка (процент); PV – сумма активов в начальный период (база начисления); FV – сумма активов в конечный период; t – количество времени (временной интервал). Тогда формула расчета суммы по методу наращения при немецкой системе расчета срока вложений будет выглядеть так:
Формула дисконтирования следует из формулы наращения и имеет следующий вид:
Полученная сумма (PV) является современной стоимостью будущей суммы (FV), которая образуется через t дней при действующей ставке процента r.
Пример. Необходимо определить современную стоимость 1 000 000 руб., которые будут получены через 3 месяца, если рыночная ставка процента равна 56% годовых. На основе формулы дисконтирования вычисляем:
Общим правилом для расчета доходности финансовых инструментов является сопоставление затрат на приобретение актива с доходом, который он генерирует. Основная формула расчета доходности легко выводится из приведенных выше формул:
Множитель
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.217.100 (0.005 с.) |

 ,
, ,
,
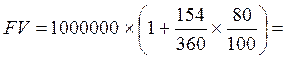 1 342 222 руб.
1 342 222 руб. 1 348 888 руб.
1 348 888 руб. 1 344 109 руб.
1 344 109 руб. ,
, .
. .
. .
. =877 192 руб.
=877 192 руб.
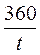 в данном случае приводит полученный за любой период времени доход к годовой размерности.
в данном случае приводит полученный за любой период времени доход к годовой размерности.


