
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, приводящие к понятию производной
Пусть в некоторой окрестности точки Определение: Приращением аргумента х в точке Определение. Приращением функции
Это приращение зависит от двух аргументов Y
0 X
Рис.1
Пример. Если т. е. при увеличении стороны квадрата, равной 1 на 0,1, его площадь возрастает на 0,21. Используя понятия Dx, Dy, можно дать ещё одно определение непрерывности функции в точке Определение. Если функция В самом деле, этот предел означает, что
Определение. Если существует предел
то это число называется производной функции Эта производная обозначается также одним из следующих символов:
Этот предел можно записывать также в виде
Определение. Функция Выясним теперь связь между дифференцируемостью и непрерывностью функции, для этого из определения выразим D f.
(где Следовательно,
Теорема. Если функция Пример. Функция
1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь S(t) (рис.2).
Рис. 2
Тогда за промежуток времени от
и средняя скорость точки на промежутке
Итак, мгновенная скорость точки в момент 1.2.Геометрический смысл производной. Через две точки
Здесь
Y
D
A
0 Рис. 3
Определение. Касательной к графику функции Другими словами, касательная
Если
В этом случае график функции в точке Таким образом, Уравнение этой касательной имеет вид
Если
1.3 Примеры непосредственного вычисления производных. Основные правила дифференцирования. Вычислим производные некоторых основных элементарных функций, исходя из определения производной. 1. Постоянная функция
2. Показательная функция
(см. эквивалентные б.м., 60). В частности, 3. Степенная функция
(см. эквивалентные бесконечно малые 70,). В частности,
4. Логарифмическая функция
В частности, 5. Тригонометрические функции
Аналогично Основные правила дифференцирования. Теорема 1. (правила дифференцирования суммы, произведения и частного). Если функции 1. 2. 3. Примеры: 1. Самостоятельно проверьте, что
Производная сложной функции и обратной функций
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.248 (0.018 с.) |
 и в самой точке
и в самой точке  .
. называется разность
называется разность  .
. в точке
в точке  .
. и Dx. Геометрически Dx и Df означают изменения абсциссы и ординаты точки на графике
и Dx. Геометрически Dx и Df означают изменения абсциссы и ординаты точки на графике 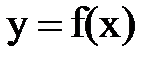 при перемещении из точки
при перемещении из точки 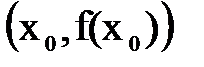 в точку
в точку  (рис.1).
(рис.1).
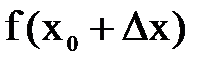 B
B A
A

 , то
, то  ,
, , эквивалентное предыдущему.
, эквивалентное предыдущему. определена в некоторой окрестности точки
определена в некоторой окрестности точки 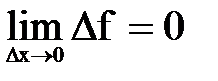 , то она называется непрерывной в точке
, то она называется непрерывной в точке 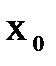 .
. , т. е.
, т. е.  .
.
 в точке
в точке  .
. .
.
 называется дифференцируемой в точке
называется дифференцируемой в точке  , если она имеет конечную производную в этой точке.
, если она имеет конечную производную в этой точке. ,
, - б.м. при
- б.м. при 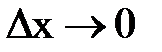 (свойство 30 б.м., модуль 3)).
(свойство 30 б.м., модуль 3)). .
.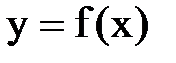 дифференцируема в точке
дифференцируема в точке  всюду непрерывна, однако она не дифференцируема при
всюду непрерывна, однако она не дифференцируема при  , так как
, так как  .
. , а этот предел, как мы выше проверяли, не существует.
, а этот предел, как мы выше проверяли, не существует.


 до
до  она проходит путь
она проходит путь ,
, равна
равна  . Мгновенная скорость
. Мгновенная скорость  точки в момент
точки в момент  равна пределу
равна пределу  при
при  .
. .
. . Это и есть механический смысл производной.
. Это и есть механический смысл производной. и
и  на графике функции
на графике функции  проведём прямую. Эта прямая называется секущей к графику функции (рис.3). Её угловой коэффициент, т. е. тангенс угла наклона к оси Ох равен
проведём прямую. Эта прямая называется секущей к графику функции (рис.3). Её угловой коэффициент, т. е. тангенс угла наклона к оси Ох равен . (1)
. (1) может быть как положительным, так и отрицательным.
может быть как положительным, так и отрицательным. B
B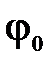

 X
X в точке
в точке  при
при  .
. в точке
в точке  - это прямая, проходящая через
- это прямая, проходящая через 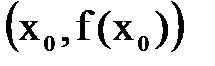 , угловой коэффициент которой
, угловой коэффициент которой .
. существует, то из (1) следует, что
существует, то из (1) следует, что .
. имеет касательную.
имеет касательную. есть угловой коэффициент касательной к графику
есть угловой коэффициент касательной к графику  в точке
в точке  (геометрический смысл производной).
(геометрический смысл производной).
 не существует, то касательной к графику функции в точке
не существует, то касательной к графику функции в точке  провести нельзя (например,
провести нельзя (например,  при
при  ).
). .
. .
.
 .
. .
. .
.
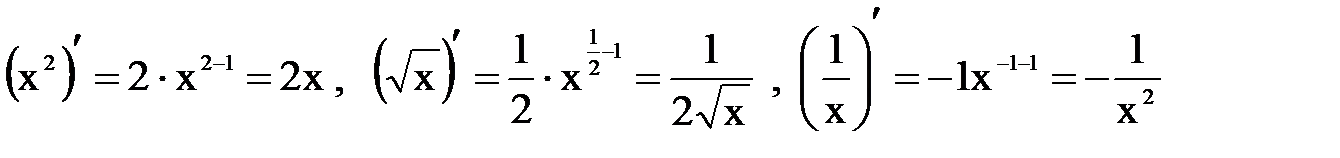 .
.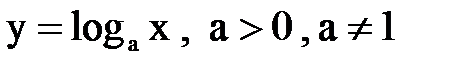 .
.
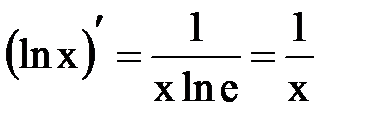 .
. .
.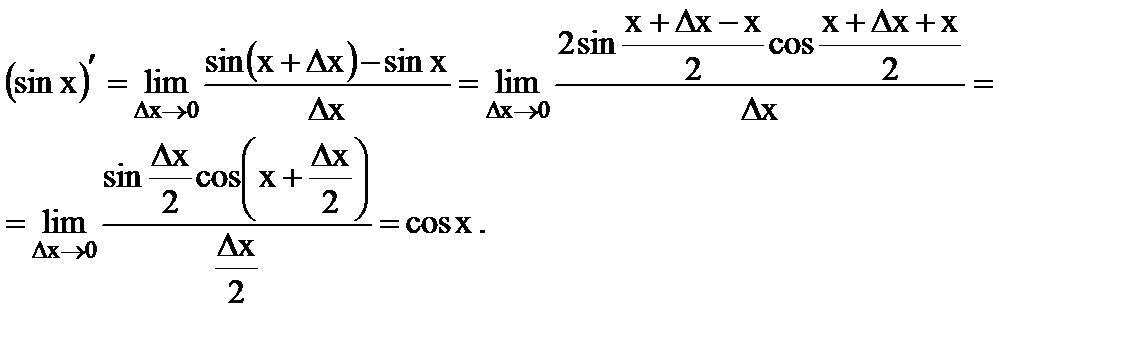
 .
. и
и  дифференцируемы в точке x, то сумма, произведение и частное этих функций (частное при условии, что
дифференцируемы в точке x, то сумма, произведение и частное этих функций (частное при условии, что  ) также дифференцируемы в этой точке и имеют место следующие формулы:
) также дифференцируемы в этой точке и имеют место следующие формулы:

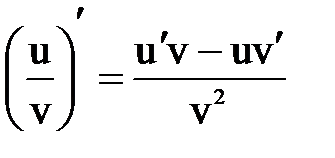 .
.
 .
.


