
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекции № 4-6 Тема 2. Векторная алгебра
Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении Аналитическая геометрия в отличие от элементарной классической геометрии, изучаемой в школе, даёт возможность решать многие геометрические задачи алгебраическими методами, которые не требуют геометрических построений. В её основе лежит понятие системы координат, которое позволяет задавать точки с помощью наборов чисел, а линии и поверхности с помощью уравнений. Определение. Координатной осью Ox на прямой называется прямая с выбранным началом координат – точкой O, направлением и масштабным единичным отрезком [0,1]. При этом каждой точке A на прямой сопоставляется число – её координата x. Соответствующее обозначение A(x ).
Рис. 2.1 Система координат на прямой
При этом имеется взаимно однозначное соответствие между всеми точками прямой и всеми действительными числами – координатами этих точек. Определение. Декартовой системой координат (Д.С.К.) на плоскости Координаты проекций точки A плоскости на эти оси называются координатами точки A в Д.С.К. Oxy. Это обозначается в виде A(x,y). При этом имеется взаимно однозначное соответствие между всеми точками плоскости и всеми парами действительных чисел – координатами этих точек (рис.2.2).
1
Рис. 2.2 Система координат на плоскости Точка O имеет координаты (0,0). Координаты точек на оси Ox имеют вид (x,0). Координаты точек и оси Oy имеют вид (О,у). Определение. Д.С.К. в пространстве Oxyz называется тройка взаимно перпендикулярных осей координат, пересекающихся в общем начале координат точке O и имеющих равные масштабные отрезки. Третья ось при этом называется осью аппликат (Oz). Координаты проекции точки A на эти три оси называются координатами точки A в Д.С.К. Oxyz (обозначение A (x,y,z); x– абсцисса, y– ордината, z– аппликата).
При этом имеется взаимно однозначное соответствие между всеми точками пространства и всеми тройками действительных чисел – координатами этих точек. Точка O имеет координаты O (0,0,0). Координаты точек на оси Ox имеют вид (x,0,0), на Oy – (0,y,0), на Oz –(0,0,z). Простейшие задачи аналитической геометрии Рассмотрим две простейшие задачи: нахождение расстояния между двумя точками и деление отрезка в данном отношении. Расстояние между точками A и B будем обозначать через |AB|. Оно обладает следующими свойствами. 1) |AB| 2) |AB|=|BA|. 3) |AC|≤|AB|+|BC|. Теорема 1. Расстояние между точками A(xA) и B(xB) на оси Ox находится по формуле |AB|=|xB–xA|. Здесь справа записан модуль разности между координатами точек B и A.
Рис.2.3 Расстояние между точками
Теорема 2. Расстояние между точками A(xA,yA) и B(xB,yB) на плоскости Oxy находится по формуле |AB|= Теорема 3. Расстояние между точками A(xA,yA,zA) и B(xB,yB,zB) в пространстве Oxyz находится по формуле
Пример. Пусть A(1,1,1),B(2,3,–1). Найдём |AB|.
Определение. Разделить отрезок AB в отношении Теорема 4. Пусть точки A(xA) и B(xB) лежат на оси Ox и точка M(xM ) делит отрезок AB в отношении Доказательство. Пусть xB>xA, тогда xA<xM<xB, |AM|=xM–xA, |MB|=xB–xM, из определения точки M получим уравнение:
Решим его. Теорема 5. Пусть точка M(xM,yM,zM) делит отрезок AB в отношении
Пример2. Найти координаты точки M,делящей отрезокAB в отношении
Следовательно,M(2,3,4). Следствие. Если точка M является серединой отрезка AB, то
Эти формулы получаются из формул теоремы 5 при a=b=1.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.41.106 (0.006 с.) |
 называется пара взаимно перпендикулярных координатных осей на этой плоскости, пересекающиеся в общем начале координат точке O и имеющие равные масштабные отрезки. Первая из этих осей называется осью абсцисс (Ox), а вторая – осью ординат (Oy).
называется пара взаимно перпендикулярных координатных осей на этой плоскости, пересекающиеся в общем начале координат точке O и имеющие равные масштабные отрезки. Первая из этих осей называется осью абсцисс (Ox), а вторая – осью ординат (Oy). 0. |AB|=0 только в том случае, когда A=B.
0. |AB|=0 только в том случае, когда A=B.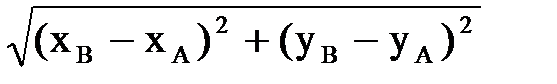 .
.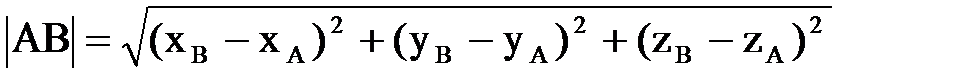 .
.
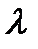
 это значит найти на нём такую точку M, что
это значит найти на нём такую точку M, что 
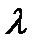 , тогда
, тогда  .
.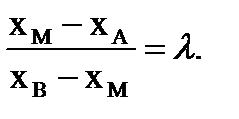


 , где A(xA,yA,zA), B(xB,yB,zB), тогда
, где A(xA,yA,zA), B(xB,yB,zB), тогда
 , где A(1,1,2), B(4,7,8). Получим:
, где A(1,1,2), B(4,7,8). Получим: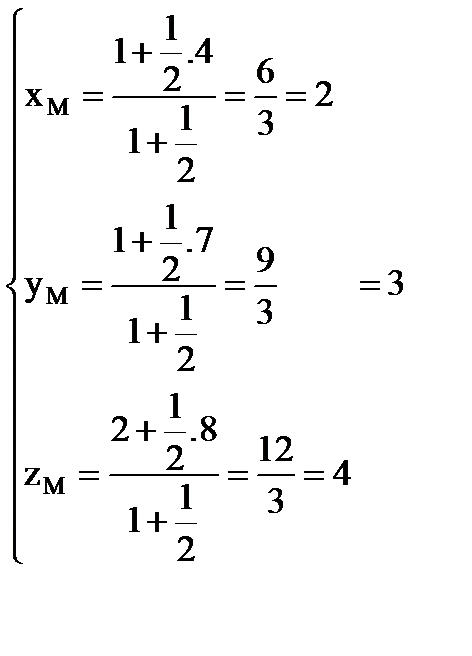 .
. .
.


