
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция. Основные свойства функций
Переменная величина, характеризующая какой-то процесс, обычно возникает не индивидуально, а в связи с другими переменными величинами. Дело в том, что процессы, протекающие в окружающем мире, являются достаточно сложными и характеризуются многими переменными величинами, связи между которыми составляют закономерности, проявляющиеся в ходе данного процесса. Кроме того, любой процесс происходит не изолированно, а во взаимодействии с другими процессами. Пример. Состояние газа при фиксированной температуре характеризуется давлением Математическую основу изучения связей между переменными величинами составляет понятие функциональной зависимости переменных величин или понятие функции. Определение. Функцией f с областью определения D и областью значений Е называется некоторое отображение из D в Е, т. е. соответствие, при котором каждому элементу Буква вой буквой слова "funktion" - "функция". Иногда функции записываются и так:
Таким образом, для того чтобы функция была определена, надо знать: а) область определения; б) закон соответствия. Обычно функция задается аналитически - какой-нибудь формулой. Иногда закон соответствия задается разными формулами на разных участках ее области определения. Примеры 1) Если D - множество всех студентов КазНТУ, а. Е - множество всех его институтов, то в качестве функции можно взять соответствие каждому студенту
2) Пусть D - множество всех векторов в пространстве, а Функция 3) Площадь круга радиуса 4) Область определения этой функции - отрезок 5) 1.2.1 Способы задания. а) Табличный. Функция может быть задана в виде таблицы. Например, пусть температуру Т воздуха измеряют через каждый час. Тогда каждому моменту времени t= 0,l,...,24 соответствует определенное число Таблица 1
Таким образом, получена функция Например, Таблица 2
соответствует и функции б) Графический. Графиком функции Пусть задана функция Y Г
0 x Рис. 6
Построение графика функции дополняет аналитический {или какой-нибудь другой) способ задания функции, так как делает наглядным ход ее изменения. Во многих технических устройствах график функции возникает и как самостоятельный способ задания функции. Приборы вычерчивают график зависимости одной величины от другой (чаще всего от времени). в) Аналитический. Аналитическим способом, т. е. с помощью одной формулы можно задавать только элементарные функции. Это самый универсальный способ задания функции, из которого можно получить и таблицу и график.
Элементы поведения функции Ограниченные величины и функции. Переменная величина
Для функции
при всех Так, например, Иногда говорят об ограниченности функции лишь на некотором интервале, являющемся частью области определения; это значит, что условие (*) выполняется для рассматриваемого интервала; число
y M
x
-M
Рис. 7 Пример.
y
x 0
Рис. 8 В то же время на любом интервале
y
M
- M
Рис. 9 Возрастание и убывание функций на интервале. Функция
y
Рис.10 1. Функция 2. Запишем эти определения с помощью логических символов - кванторов: для интервала 3. Интервал, на котором функция возрастает или убывает, называется интервалом монотонности этой функции, а про функцию говорят, что она монотонна на этом интервале.
y
0
Рис. 11 Пример 10. y
x 0 Рис.12 Четные и нечетные функции. Пусть задана функция
функция
Примеры: 1. 2. 3. 4. Из тригонометрии известно, что 5. Геометрически четность функции означает, что ее график симметричен относительно оси ординат. Действительно, наряду с точкой
y
x -x o x Рис. 13 Таким образом, наряду с произвольной точкой
y
Четная функция
0 x
Рис. 14 Рассуждая аналогичным образом, можно установить, что график нечетной функции симметричен относительно начала координат (рис.15).
y
0 x
Рис. 15 Примеры: 1. 2.
Период. Периодические функции. Число
Функция Если число Пример. Из тригонометрии известно, что периоды функций График периодической функции с периодом Пример. Периодична ли функция Это противоречит нашему предположению о существовании периода, значит, предположение неверно. Функция
y 0 l x Рис.16
1.3.1. Сложная функция (функция от функции). Пусть дана функция
Возьмем какое-либо значение
x
tt
Рис.17 На рис. 17 переменные Получаем
Область определения функции
x Область значений функции
t Область определения функции
y
? Область значений функции
x
Область определения функции
t
Область определения функции
Рис.19
Примеры: 1. 2. Сложные функции могут быть образованы и из большего числа составляющих. Примеры: 1. у = x3; x = sint, t = 3w + l; у = F(w) = (sin(3w + l))3 - Здесь два промежуточных аргумента х и t, независимая переменная w. 2. 1.3.2. Обратная функция. Пусть на некотором интервале X задана функция Если f и
Графиком функции
Рис. 20 Рис. 21 Примеры: 1. 2.
Рис.22 Рис.23
Функция
обратные функции к Примеры:
1.
обратные функции к 2.
обратные функции к
График обратной функции При таком перегибании плоскости график нашей функции отобразится симметрично относительно биссектрисы первого и третьего координатных углов (рис.24). На рис.25 показаны графики взаимно обратных функций
Рис.24 Рис.25 1.3.3.Неявные функции. Иногда функциональная зависимость величин у и х задается некоторым уравнением, связывающим х и у, но нерешенным ни относительно у, ниотносительно х. Например, уравнение прямой
где буква F "скрывает" те операции над х и у, которые следует проделать в основной (левой) части уравнения. Исследовать неявные функции почти всегда труднее. 1.3.4. Параметрическое задание функции. Кривые на плоскости часто задаются параметрическими уравнениями. В этих уравнениях координаты х и у точки на кривой выражены как функции третьего, вспомогательного переменного t (параметра):
Это новый, иногда наиболее удобный, способ задать функциональную зависимость между х и у. Считаем, что функция
т.е. у есть функция от х (сложная функция). Примеры: 1) 2)
параметрические уравнения: 1) окружности радиуса Весьма часто параметрическое задание линии возникает в механике. Там x и у - координаты движущейся точки, меняющиеся в зависимости от времени t, а линия - траектория этой точки.
Контрольные вопросы:
1. Дайте определение функции. Что называется областью определения функции? 2. Какая функция называется элементарной, сложной? Приведите примеры. 3. Четность, нечетность функция 4. Период и периодичность функции 5. Операции над множествами, их свойства 6. Область определения произведения и суммы функции
Литература:
Основная [2] Глава 1 § 1.1-1.11 стр. 9-31 Глава 2 § 2.1-2.12 стр. 34-64 Глава 3 § 3.1-3.2 стр. 66-85 [19] 2.1-2.4 стр. 138-162
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.14.219 (0.219 с.) |
 и объемом
и объемом  , занятым газом. Эти переменные величины связаны зависимостью
, занятым газом. Эти переменные величины связаны зависимостью  , где
, где  - постоянная (закон Бойля-Мариотта).
- постоянная (закон Бойля-Мариотта). сопоставляется единственный элемент
сопоставляется единственный элемент  .
. (или
(или  ) употребляется для обозначения функции чаще других, так как является пер-
) употребляется для обозначения функции чаще других, так как является пер- ;
;  и т.д. При таких записях как бы "экономят" букву: и значение функции, и закон соответствия обозначают одной буквой. Понятие функции является основным понятием математического анализа. Что надо знать, чтобы была задана функция? Прежде всего, должна быть известна область значений аргумента
и т.д. При таких записях как бы "экономят" букву: и значение функции, и закон соответствия обозначают одной буквой. Понятие функции является основным понятием математического анализа. Что надо знать, чтобы была задана функция? Прежде всего, должна быть известна область значений аргумента  . Эта область значений аргумента называется областью определения функции. Затем мы должны знать, как по любому значению
. Эта область значений аргумента называется областью определения функции. Затем мы должны знать, как по любому значению  , согласно которому по любому значению
, согласно которому по любому значению  .
. сопоставляет каждому вектору
сопоставляет каждому вектору  D его модуль у
D его модуль у  Область определения этой функции
Область определения этой функции  , т.е.
, т.е.  ; закон соответствия задан формулой
; закон соответствия задан формулой  .
.
 ; закон соответствия задан разными формулами на разных участках:
; закон соответствия задан разными формулами на разных участках:  при
при  и
и 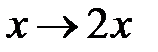 при
при 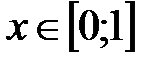 .
.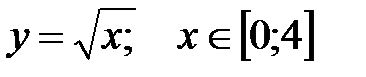 . Область определения [0;4]. Область значений [0;2].
. Область определения [0;4]. Область значений [0;2]. (таблица 1):
(таблица 1):


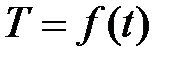 , определённая на множестве целых чисел от 0 до 24, заданная таблицей. Этот способ не даёт полной характеристики функции, поскольку в таблицу часто невозможно внести все точки из области определения функции.
, определённая на множестве целых чисел от 0 до 24, заданная таблицей. Этот способ не даёт полной характеристики функции, поскольку в таблицу часто невозможно внести все точки из области определения функции. и
и  .
. таких, что
таких, что  и
и  . График даёт наглядное представление о характере поведения функции.
. График даёт наглядное представление о характере поведения функции. точек на плоскости
точек на плоскости 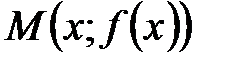 , абсциссами которых являются значения аргумента
, абсциссами которых являются значения аргумента  , а ординатами -соответствующие значения функции
, а ординатами -соответствующие значения функции  . Множество
. Множество  называется графиком функции
называется графиком функции 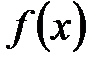 .
.
 , что все значения
, что все значения  . Иными словами, для всех значений
. Иными словами, для всех значений 
 (*)
(*) (рис. 7)
(рис. 7) ограниченная функция, так как
ограниченная функция, так как 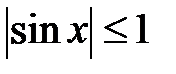 при всех
при всех  может зависеть от взятого интервала.
может зависеть от взятого интервала. - функция, не являющаяся ограниченной. В самом деле, какое бы
- функция, не являющаяся ограниченной. В самом деле, какое бы  мы не взяли, для тех
мы не взяли, для тех  будет выполняться неравенство
будет выполняться неравенство  (рис.8).
(рис.8).
 x
x эта функция ограничена:
эта функция ограничена: 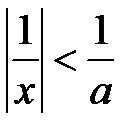 (рис.9). Число
(рис.9). Число  зависит от этого интервала.
зависит от этого интервала.
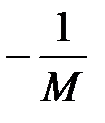 - x 0
- x 0
 x
x
 называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует большее значение функции (рис.10).
называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует большее значение функции (рис.10).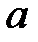 x1 x2
x1 x2 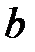 x
x - условие возрастания;
- условие возрастания;  - условие убывания.
- условие убывания. (рис.12). Интервалы монотонности: на
(рис.12). Интервалы монотонности: на 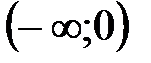 функция убывает; на
функция убывает; на  функция возрастает.
функция возрастает.
 с областью определения
с областью определения  . Функция
. Функция 
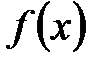 называется нечетной, если
называется нечетной, если
 . Область определения
. Область определения 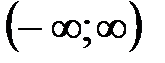 симметрична относительно начала координат
симметрична относительно начала координат  . Функция четная.
. Функция четная. . Область определения
. Область определения  . Область определения
. Область определения  (два интервала) симметрична относительно начала координат (множество всех действительных чисел с выброшенным нулем).
(два интервала) симметрична относительно начала координат (множество всех действительных чисел с выброшенным нулем).  . Функция нечетная.
. Функция нечетная. - нечетные функции;
- нечетные функции;  - четная функция.
- четная функция.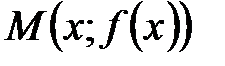 график содержит точку
график содержит точку  , так как
, так как  , точка
, точка  имеет координаты
имеет координаты  . Точки
. Точки 
 (рис.14).
(рис.14).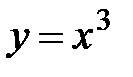
 ; Пусть
; Пусть  и
и  , тогда,
, тогда,  т.е.
т.е.  и
и  . Значит, рассматриваемая функция не является ни четной, ни нечетной.
. Значит, рассматриваемая функция не является ни четной, ни нечетной. Пусть
Пусть 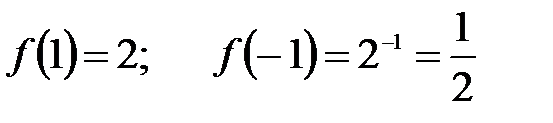 , т.е.
, т.е. 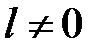 называется периодом функции
называется периодом функции 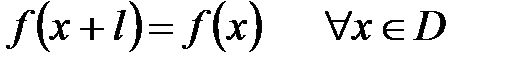
 и
и 
 - период функции
- период функции  , т.е. число
, т.е. число  где
где  будет периодом
будет периодом  , т.е.
, т.е.  - период;
- период; 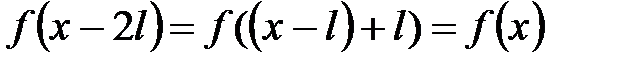 , т.е.
, т.е.  тоже период. В дальнейшем название периода функции будем применять к наименьшему положительному периоду.
тоже период. В дальнейшем название периода функции будем применять к наименьшему положительному периоду. и
и  , а периоды
, а периоды  равны
равны  .
.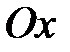 на
на  и т. д. (рис. 16).
и т. д. (рис. 16). (показательная)? Допустим, что периодична. Тогда
(показательная)? Допустим, что периодична. Тогда  , при этом для любого
, при этом для любого  ; отсюда
; отсюда 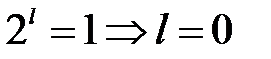 .
. :
: . Полученному значению
. Полученному значению 
 ( рис.17 )
( рис.17 )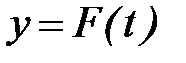

 откладываются на трех осях, изображенных параллельно. В конечном итоге взятому значению
откладываются на трех осях, изображенных параллельно. В конечном итоге взятому значению  , т.е. переменная
, т.е. переменная  оказалась функцией независимой переменной
оказалась функцией независимой переменной  . Функция
. Функция  называется сложной функцией от независимой переменной
называется сложной функцией от независимой переменной  от функции
от функции  ). При этом функция
). При этом функция  - промежуточным аргументом. Функции
- промежуточным аргументом. Функции  называют еще составляющими для сложной функции
называют еще составляющими для сложной функции 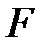 ; говорят также, что
; говорят также, что 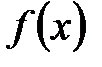 образовать нельзя (рис. 19). В таких случаях сложную функцию (или функцию от функции) можно задать только для тех значений независимой переменной
образовать нельзя (рис. 19). В таких случаях сложную функцию (или функцию от функции) можно задать только для тех значений независимой переменной  y
y
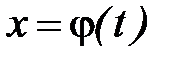

 Рис.18
Рис.18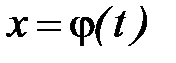
 . Область значений промежуточной переменной
. Область значений промежуточной переменной  - отрезок [-1;1]; он не укладывается в область определения внешней функции
- отрезок [-1;1]; он не укладывается в область определения внешней функции  [ее область определения
[ее область определения 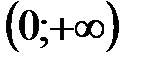 ]. Поэтому сложную функцию
]. Поэтому сложную функцию  можно образовать только для тех значений аргумента
можно образовать только для тех значений аргумента  , для которых
, для которых  .
.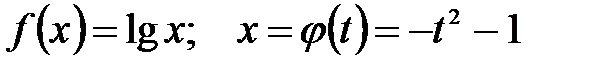 . Здесь область значений промежуточного переменного
. Здесь область значений промежуточного переменного  , а область определения внешней функции
, а область определения внешней функции  . Значит, в этом случае образовать сложную функцию [т.е. суперпозицию функций
. Значит, в этом случае образовать сложную функцию [т.е. суперпозицию функций 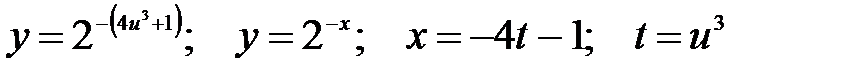 .
. соответствует определенное значение
соответствует определенное значение  . Если же интервал X является интервалом монотонности для f(x), то и каждомузначению
. Если же интервал X является интервалом монотонности для f(x), то и каждомузначению  отвечает одно вполне определенное значение
отвечает одно вполне определенное значение  может рассматриваться и как функция
может рассматриваться и как функция  , т.е.
, т.е.  - взаимно обратные функции, то имеют место тождества (рис.21)
- взаимно обратные функции, то имеют место тождества (рис.21)

 - обратная к ней функция. Областью определения функции у = 2х является
- обратная к ней функция. Областью определения функции у = 2х является 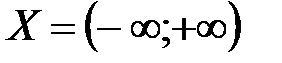 , этот же интервал является областью значений обратной функции
, этот же интервал является областью значений обратной функции  . Областью значений функции
. Областью значений функции  служит интервал
служит интервал 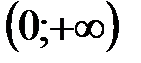 , он же является областью определения для
, он же является областью определения для  (рис.17).
(рис.17).
 несколько неудобна тем, что, вопреки привычному, ее аргументом является
несколько неудобна тем, что, вопреки привычному, ее аргументом является  , а не
, а не  . Неудобство это скорее психологического характера, однако, чтобы его избежать, наряду с функцией
. Неудобство это скорее психологического характера, однако, чтобы его избежать, наряду с функцией  , которую также называют обратной функцией к функции
, которую также называют обратной функцией к функции  . Функция
. Функция  получается из
получается из 


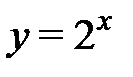


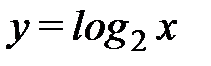 .
.
 Правда, его очень просто решить относительно у:
Правда, его очень просто решить относительно у:  , и мы получаем обычное задание функции. Однако уравнение, связывающее х и у, не всегда удается разрешить относительно у или х. Таково, например, уравнение
, и мы получаем обычное задание функции. Однако уравнение, связывающее х и у, не всегда удается разрешить относительно у или х. Таково, например, уравнение  . Однако и здесь значениям х отвечают определенные значения у (например, значению х = 0 отвечает у = -2). В таких случаях говорят, что функция у - неявная функция от х, она задана уравнением, связывающим x и у. Подобным образом задаются многие кривые в аналитической геометрии. Например,
. Однако и здесь значениям х отвечают определенные значения у (например, значению х = 0 отвечает у = -2). В таких случаях говорят, что функция у - неявная функция от х, она задана уравнением, связывающим x и у. Подобным образом задаются многие кривые в аналитической геометрии. Например,  - уравнение окружности (с центром в начале координат и радиуса
- уравнение окружности (с центром в начале координат и радиуса  ). Здесь можно явно выразить у через х:
). Здесь можно явно выразить у через х:  , но получаются две функции, соответствующие "+" или "-" перед корнем (верхняя и нижняя полуокружности). Точно так же уравнение эллипса
, но получаются две функции, соответствующие "+" или "-" перед корнем (верхняя и нижняя полуокружности). Точно так же уравнение эллипса  заданием неявной функции. В самом общем виде уравнение, задающее неявную функцию, можно записать как
заданием неявной функции. В самом общем виде уравнение, задающее неявную функцию, можно записать как

 имеет обратную:
имеет обратную:  . [т.е. решаем уравнение
. [т.е. решаем уравнение  ]. Поставив это во второе уравнение, получим:
]. Поставив это во второе уравнение, получим:


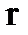 , 2) эллипса с полуосями а и b.
, 2) эллипса с полуосями а и b.


