
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространства. Координаты вектора
Векторы используются для описания величин, имеющих определённое направление. Примерами таких величин являются сила, скорость, перемещение. Определение. Вектором называется отрезок с выбранным направлением, или направленный отрезок. Вектор с началом в точкеA и с концом в точкеB обозначается через Вектор, у которого начало совпадает с его концом, называется нулевым вектором и обозначается через Векторы Два вектора Линейными операциями над векторами называются умножение вектора на число и сложение векторов. Определение. Произведением вектора 1) | a 2) a 3) Вектор a Пример1. Ниже изображены вектора
Рис. 2. 4 Умножения вектора на число Определение. Суммой векторов
Если вектора Суммой векторов
Пример2. Если вектора
Эти линейные операции над векторами обладают следующими свойствами. 1. 1× 2. 0× 3. 4. 5. 6. 7. Операция разности векторов Определение. Разностью векторов
§ 2.4. Базис векторного пространства. Координаты вектора
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано для строк матрицы. Определение. Линейной комбинацией векторов Эта комбинация обладает двумя основными свойствами. 1) Если векторы Векторы 2) Если векторы Определение. Векторы В противном случае векторы Определение. Совокупность n линейно независимых векторов называется базисом. Множество всех плоских или пространственных векторов в которых определены операции сложения векторов и умножение вектора на число, являются простейшими примерами векторного пространства. Определение. Множество векторов, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше семи свойствам называется векторным пространством. Оказывается, что в любом векторном пространстве всегда можно выбрать несколько векторов, из которых с помощью линейных комбинаций однозначно можно получить любой вектор этого пространства и которые являются базисными.
Определение. Любой ненулевой вектор базисным вектором этой прямой. Любая пара неколлинеарных векторов Теорема о базисе. Любой вектор 1) на прямой: 2) на плоскости: 3) в пространстве: Доказательство. 1) Случай прямой. Пусть вектор
2) Случай плоскости. Пусть векторы Проведём через вектора
П
Координату точки A1 наOx обозначим через x, а координату точки A2 на Oy – черезy. Тогда, используя определение суммы векторов и предыдущий случай, получим: 3) Случай пространства. Отложим вектора
Проверим, что коэффициенты (x, y, z) линейной комбинации определяется однозначно. Допустим противное, пусть вектор Здесь справа стоит вектор, выражающий диагональ параллелограмма или параллелепипеда, или отрезок на одной из осей Ox, Oy, Oz, который не является нулевым. Противоречие. Из последнего рассуждения следует, что базисные вектора линейно независимы. Определение. Коэффициенты линейной комбинации базисных векторов, выражающие вектор Вектор, лежащий на прямой, имеет одну координату x, на плоскости – две координаты x, y; в пространстве – три координаты x, y, z. Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор
Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
Пусть в пространстве имеется декартова система координат Oxyz. С ней связан стандартный базис из единичных взаимно перпендикулярных векторов, расположенных вдоль осей Ox, Oy, Oz. Эти
базисные ве
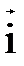 , ,  , ,  . .
Выясним связь между введёнными ранее понятиями координат точки в системе Oxyz и вектора в базисе { Определение. Вектор, начало которого находится в начале координат,а конец в точке A, т.е. вектор Если (x,y,z) – координаты точки A в системеOxyz, то радиус–вектор Теорема. Пусть в декартовой системе координат Oxyz заданы две точки A(xA,yA,zA) и B(xB,yB,zB), тогда в базисе { Доказательство. Запишем вектор
и воспользуемся результатом предыдущей теоремы для базиса {
Пример3. ПустьA(1,–1,1), B(2,3,4), тогда в базисе {
Иногда координаты вектора в базисе { Определение. Проекцией вектора
При параллельном переносе вектора, его проекция на ось L не меняется. Проекция обозначается символами Отсюда получим следующую теорему. Теорема. Пусть вектор
Определение. Проекцией вектора
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.145 (0.498 с.) |
 , кроме того, вектор можно обозначать одним символом, например
, кроме того, вектор можно обозначать одним символом, например 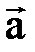 .
. . Длина отрезка, изображающего вектор
. Длина отрезка, изображающего вектор  , называется модулем этого вектора и обозначается |
, называется модулем этого вектора и обозначается | 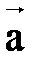 |.
|.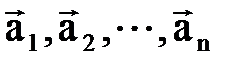 , параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору.
, параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. и
и  считаются равными, если они равны по модулю, коллинеарны и одинаково направлены. Из этого определения следует, что при параллельном переносе вектор не меняется, по этому в качестве начала вектора можно выбрать любую точку.
считаются равными, если они равны по модулю, коллинеарны и одинаково направлены. Из этого определения следует, что при параллельном переносе вектор не меняется, по этому в качестве начала вектора можно выбрать любую точку. на число a называется такой вектор a
на число a называется такой вектор a  , что выполняются три условия.
, что выполняются три условия. |=| a ||
|=| a ||  |
| ||
||  сонаправлен вектору
сонаправлен вектору  ; –2
; –2  .
.


 и
и 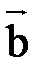 , исходящих из одной точки, называется вектор, совпадающий с диагональю параллелограмма, образованного векторами
, исходящих из одной точки, называется вектор, совпадающий с диагональю параллелограмма, образованного векторами  и
и  , исходящий из той же точки.
, исходящий из той же точки.


 и
и  не исходят из одной точки, то их начала необходимо с помощью параллельного переноса перенести в одну точку. Это определение называется правилом параллелограмма. При сложении большого числа векторов удобнее пользоваться следующим определением, равносильным предыдущему.
не исходят из одной точки, то их начала необходимо с помощью параллельного переноса перенести в одну точку. Это определение называется правилом параллелограмма. При сложении большого числа векторов удобнее пользоваться следующим определением, равносильным предыдущему. ,
,  ,...,
,..., 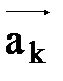 , у которых начало
, у которых начало  вектора совпадает с концом
вектора совпадает с концом  (i=2¸k), является вектор, соединяющий начало вектора
(i=2¸k), является вектор, соединяющий начало вектора  .
.

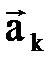
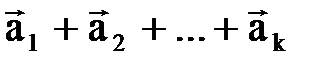
 ,
,  ,
,  совпадают с тремя рёбрами параллелепипеда исходящими из одной вершины, то их сумма
совпадают с тремя рёбрами параллелепипеда исходящими из одной вершины, то их сумма  +
+  +
+  совпадает с диагональю этого параллелепипеда, исходящей из той же вершины (рис.2.6)
совпадает с диагональю этого параллелепипеда, исходящей из той же вершины (рис.2.6)



 =
= 


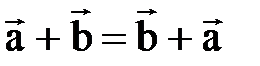

 a
a и
и  сводится к двум линейным операциям:
сводится к двум линейным операциям:  , однако часто удобней пользоваться следующим специальным определением, равносильным вышеприведённому.
, однако часто удобней пользоваться следующим специальным определением, равносильным вышеприведённому.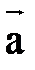 и
и  , исходящих из одной точки называется вектор, соединяющий конец вектора
, исходящих из одной точки называется вектор, соединяющий конец вектора 
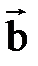

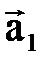 ,
,  ,...,
,...,  с коэффициентами C1,C2,...,Cn называется вектор C1
с коэффициентами C1,C2,...,Cn называется вектор C1  +C2
+C2  +...+Cn
+...+Cn 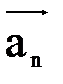 .
. ,...,
,...,  коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой.
коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой. на прямой называется
на прямой называется плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов
плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов  называется базисом пространства.
называется базисом пространства. (на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,
(на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,


 лежит на прямой L,
лежит на прямой L,  – базисный вектор этой прямой. Отложим вектора
– базисный вектор этой прямой. Отложим вектора  и
и  из некоторой точки O на прямой, вектор
из некоторой точки O на прямой, вектор  =x
=x  , т.е.
, т.е. 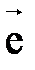 .
.

 и
и  лежат в плоскости
лежат в плоскости  .Отложим их из некоторой точки O этой плоскости, конец вектора
.Отложим их из некоторой точки O этой плоскости, конец вектора  и
и  оси Ox и Oy с единичными отрезками
оси Ox и Oy с единичными отрезками и
и 


 =
=  +
+ 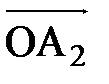 =x
=x  ,
,  и
и  из некоторой точки O, через вектора
из некоторой точки O, через вектора  проведём оси Ox, Oy, Oz. Из конца вектора
проведём оси Ox, Oy, Oz. Из конца вектора  =
=  +
+  +
+  =x
=x  .
.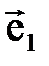



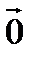 = (x 1- x 2)
= (x 1- x 2) 

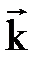
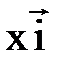



 ,
,  ,
,  }.
}. , называется радиус–вектором точки A.
, называется радиус–вектором точки A. можно записать в виде
можно записать в виде  =x
=x  +y
+y  +z
+z  . Поэтому координаты точки A(x,y,z) в системе Oxyzи вектора
. Поэтому координаты точки A(x,y,z) в системе Oxyzи вектора  в базисе {
в базисе {  ,
, 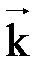 } – это одни и те же числа.
} – это одни и те же числа. ,
, 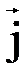 ,
,  } вектор
} вектор  имеет координаты ((xВ– xА),(yВ–yА),(zВ–zА)).
имеет координаты ((xВ– xА),(yВ–yА),(zВ–zА)). в виде:
в виде: =
= 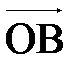 –
–  =
=  +(–1)
+(–1) 
 }, получим:
}, получим: .
. ,
,  ,
,  }
} =
=  +4
+4  +3
+3  , т.е.
, т.е.  ={1,4,3}.
={1,4,3}. ,
, 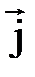 ,
,  } удобно представлять себе в виде проекций.
} удобно представлять себе в виде проекций. на координатную ось L называется длина проекции вектора
на координатную ось L называется длина проекции вектора  на L, взятая со знаком “+”, если угол между
на L, взятая со знаком “+”, если угол между 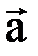 и положительным направлением оси острый, и “–“, если он тупой.
и положительным направлением оси острый, и “–“, если он тупой.
 L
L 

 . Несложно проверить, что
. Несложно проверить, что  =
=  и
и  =
=  +
+ 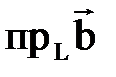 . Очевидно, что если
. Очевидно, что если  имеет координаты
имеет координаты  то
то 
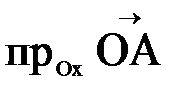 ,
, 
 ,
, 
 .
. имеет координаты
имеет координаты  в базисе
в базисе  , тогда
, тогда 
 ,
, 
 ,
, 
 .
.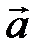 на ненулевой вектор
на ненулевой вектор  (обозначение
(обозначение  ) называется его проекция на ось L, проведенная через вектор
) называется его проекция на ось L, проведенная через вектор  (см. рис. 2.14).
(см. рис. 2.14).






