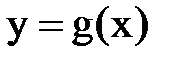Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел переменной величины. Предел последовательности.
Из разнообразных способов поведения переменных величин наиболее важен тот, при котором переменная величина стремится к некоторому пределу. В этом случае значения, принимаемые переменной величиной х, становятся сколь угодно близкими к некоторому постоянному числу a - пределу этой переменной величины. Говорят, что переменная величина стремится, неограниченно приближается к постоянному числу а (своему пределу). Дадим более подробно соответствующее определение. Переменная величина х стремится к пределу a (a - постоянное число), если абсолютная величина То же самое определение можно сказать и другими словами. Определение. Постоянное число а называется пределом переменной величины х, если Тот факт, что число а, является пределом переменной величины, записывается следующим образом:
Уточним, что следует понимать под словами "величина Переменная величина Определение предела имеет простой геометрический смысл: неравенство Необходимо представлять себе процесс приближения к пределу в динамике. Взяли некоторую
рис. 1 Введя определение предела переменной величины, мы постарались его подробно обсудить и расшифровать. Однако в этом определении осталась нераскрытой одна, весьма существенная, деталь; что следует понимать под словами "начиная с некоторого момента в изменении переменной величины Предел последовательности. Прежде всего необходимо вспомнить определение последовательности: если все значения, принимаемые переменной величиной х, можно занумеровать помощью всевозможных натуральных чисел х},х2,...хп,..., причем значение с большим номером принимается после значения с меньшим номером, то говорят, что переменная х пробегает последовательность значений хх,х2,...хп ...; или просто, что имеется последовательность (числовая последовательность). Определение. Числовой последовательностью называется действительная функция натурального аргумента, т. е. функция, у которой Она обозначается символом
Примеры: а) Последовательность
б)
в)
г) Для последовательностей содержащееся в общем определении предела переменной высказывание "начиная с некоторого момента в изменении
Определение. Число а называется пределом последовательности Соответствующее обозначение
Неравенство
x1 x2
Рис. 2 Число Будем записывать определение предела с помощью логических символов (кванторов). Определение предела последовательности с помощью кванторов выглядит так:
В рассмотренных выше примерах предел имеют последовательности а) и г), а последовательности б) и в) пределов не имеют. Пример. Доказать, что Зададим произвольное Решим это неравенство относительно Итак, для произвольного
Рис. 3 Это и означает по определению, что (Рис. 3)
Предел функции
Дадим определения пределов функции при
Пусть функция Определение. Число А называется пределом функции
(Обозначается
Рис.4
Определение. Число А называется пределом слева функции
если (Обозначается Определение. Число А называется пределом справа функции если (Обозначается Теорема. Пример. В этом примере рассматривается только
Определение. Число А называется пределом функции
(Обозначается Определение. Число А называется пределом функции (Обозначается Определение. Число А называется пределом функции Последнее определение подразумевает, что
Теорема. Предел Примеры:
Докажем, что
Свойства функций и последовательностей, имеющих предел. Рассматриваемые ниже свойства справедливы для всех видов пределов функций и пределов последовательности. Однако для краткости будем формулировать их для одного предела (при 1) Предел постоянной функции (или последовательности) равен этой постоянной, т. е.
2) Если предел функции (последовательности) существует, то он единствен.
Определение. Функция Функция, ограниченная сверху и снизу в D, называется ограниченной в D. Если D не упоминается, то подразумевается, что D=R.
Рис.5 Примеры: 1) Функция 2) Функция Определение. Последовательность Примеры: 1. 2. 3) Если функция При существовании пределов
4) Любая последовательность, имеющая предел, ограничена. Определение. Функция (а,
Если
то такая функция называется невозрастающей (убывающей) в (а, Определение. Последовательность
Примеры: 1. Любая постоянная функция или последовательность не возрастает и не убывает. Функция Теорема. Пусть функция монотонно возрастает (убывает) на интервале (а,
Здесь число
Рис.6 Если последовательность Аналогичное утверждение можно сформулировать для Теорема. Пусть в некоторой окрестности точки
Рис.7
Сформулируйте и докажите аналогичные утверждения для последовательностей.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.174.76 (0.091 с.) |
 разности между х и а становится в процессе изменения переменной величины сколь угодно малой..
разности между х и а становится в процессе изменения переменной величины сколь угодно малой.. (
( - первые буквы слова limes - предел) или х — > a
- первые буквы слова limes - предел) или х — > a , тогда, если, начиная с некоторого момента в изменении переменной величины х, значения
, тогда, если, начиная с некоторого момента в изменении переменной величины х, значения  .
. стремится к пределу
стремится к пределу  , если для любого положительного
, если для любого положительного  . начиная с некоторого момента в изменении переменной
. начиная с некоторого момента в изменении переменной 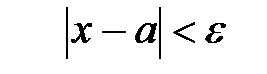 .
. означает, что
означает, что  находится в
находится в  -окрестности точки
-окрестности точки 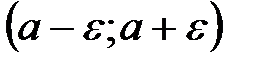 (рис. 26). Таким образом, определение предела в геометрической форме: число
(рис. 26). Таким образом, определение предела в геометрической форме: число  - окрестность точки a; начиная с некоторого момента в изменении
- окрестность точки a; начиная с некоторого момента в изменении  - окрестность точки a
- окрестность точки a  ; начиная с некоторого (более отдаленного в сравнении с первым) момента в изменении
; начиная с некоторого (более отдаленного в сравнении с первым) момента в изменении 
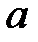




 "? Это ясно тогда, когда процесс изменения переменной протекает во времени: начиная с некоторого момента (времени). Но не всегда мы имеем дело с переменными величинами, изменение которых протекает во времени. Как же быть в этих случаях? Выход состоит в расшифровке этого места в общем определении предела переменной специфическим образом для каждого типа переменных величин: по-своему для последовательностей, по-своему для функций и т.д.
"? Это ясно тогда, когда процесс изменения переменной протекает во времени: начиная с некоторого момента (времени). Но не всегда мы имеем дело с переменными величинами, изменение которых протекает во времени. Как же быть в этих случаях? Выход состоит в расшифровке этого места в общем определении предела переменной специфическим образом для каждого типа переменных величин: по-своему для последовательностей, по-своему для функций и т.д. = N и ЕÌR.
= N и ЕÌR. , где
, где 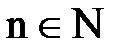 , или короче,
, или короче, 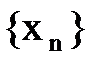 . Число
. Число 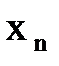 , зависящее от n, называется n – ым членом последовательности. Расставив значения последовательности по порядку номеров, получаем, что последовательность можно отождествить со счётным набором действительных чисел, т. е.
, зависящее от n, называется n – ым членом последовательности. Расставив значения последовательности по порядку номеров, получаем, что последовательность можно отождествить со счётным набором действительных чисел, т. е. .
. является постоянной и состоит из равных чисел (единиц):
является постоянной и состоит из равных чисел (единиц): 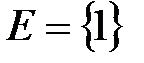 ;
; . Для неё
. Для неё 
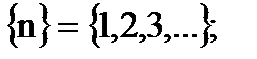
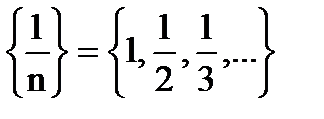 .
. , если для любого числа
, если для любого числа  найдётся число
найдётся число  , что все числа
, что все числа  , у которых
, у которых  , удовлетворяют неравенству
, удовлетворяют неравенству  .
. .
.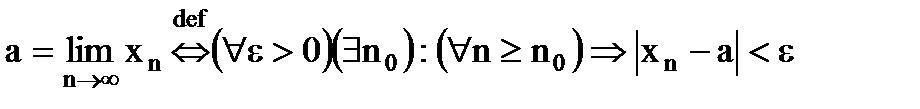 .
.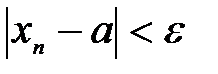 можно также записывать в виде
можно также записывать в виде  или
или  . В этих записях подчеркнуто, что величина хп становится сколь угодно мало отличимой от a, когда номер члена
. В этих записях подчеркнуто, что величина хп становится сколь угодно мало отличимой от a, когда номер члена  неограниченно возрастает. Геометрически определение предела последовательности означает следующее: для сколь угодно малой
неограниченно возрастает. Геометрически определение предела последовательности означает следующее: для сколь угодно малой  .
. xN+1 a xN+2
xN+1 a xN+2 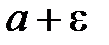 xN x3
xN x3 в нашем определении зависит от
в нашем определении зависит от  то найдется, вообще говоря, другой номер Nx > N, такой, что неравенство
то найдется, вообще говоря, другой номер Nx > N, такой, что неравенство 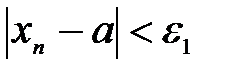 , выполняется при всех
, выполняется при всех  .
.
 .
. . В соответствии с определением мы должны найти такое число
. В соответствии с определением мы должны найти такое число  выполняется неравенство
выполняется неравенство  .
. . В качестве
. В качестве  .
. найдено число
найдено число  , что
, что  выполняется неравенство
выполняется неравенство .
.



 .
.
 .
. определена в некоторой окрестности точки а, кроме, быть может, этой точки.
определена в некоторой окрестности точки а, кроме, быть может, этой точки. при
при 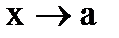 , если для каждого
, если для каждого  найдётся такое d>0, что для всех
найдётся такое d>0, что для всех 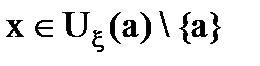 выполняется неравенство
выполняется неравенство  , т. е.
, т. е.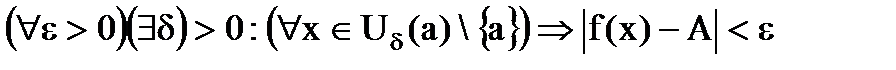 .
. или
или 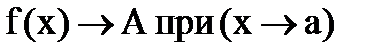



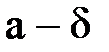
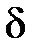



 при
при  ,
, .
. или
или  ).
). при
при  ,
, .
. или
или  ).
). существует в том и только в том случае, когда существуют пределы
существует в том и только в том случае, когда существуют пределы  , и они равны между собой.
, и они равны между собой. .
. , поэтому
, поэтому  .
. .
.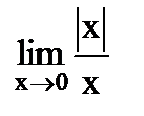 не существует, поскольку
не существует, поскольку 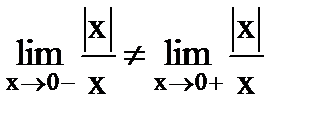 .
. при
при  , если для каждого e>0 найдётся такое число N, что при любом
, если для каждого e>0 найдётся такое число N, что при любом  выполняется
выполняется  , т. е.
, т. е. .
. ).
).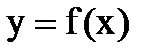 при
при  , если
, если 
 .
. .
. при
при  , если
, если  . (Обозначается
. (Обозначается  ).
). определена в некотором интервале
определена в некотором интервале 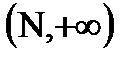 , пятое определение подразумевает, что она определена в интервале
, пятое определение подразумевает, что она определена в интервале  , а из шестого определения следует, что она определена при
, а из шестого определения следует, что она определена при  и
и 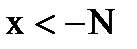 , т. е. в промежутках
, т. е. в промежутках  .
. существует в том и только в том случае, когда существуют
существует в том и только в том случае, когда существуют  и они равны между собой.
и они равны между собой. ;
; 
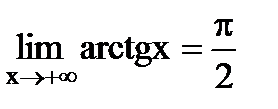 . Для
. Для 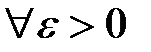 возьмем
возьмем  , тогда при
, тогда при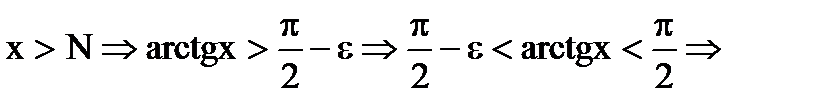

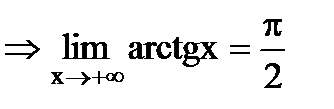 .
. ).
). .
. называется ограниченной сверху в промежутке D, если найдётся такое число С, что для всех x принадлежащих D,
называется ограниченной сверху в промежутке D, если найдётся такое число С, что для всех x принадлежащих D, 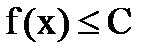 . Если
. Если  , то такая функция называется ограниченной снизу в D.
, то такая функция называется ограниченной снизу в D.

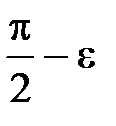
 ограничена, т. к.
ограничена, т. к. 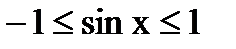 для всех x.
для всех x. ограничена снизу, но не сверху. На промежутке
ограничена снизу, но не сверху. На промежутке  она ограничена.
она ограничена. называется ограниченной (сверху, снизу), если найдётся такое С, что для всех
называется ограниченной (сверху, снизу), если найдётся такое С, что для всех  ,
,  , (или
, (или  , или
, или  ).
). – ограничена.
– ограничена. – ограничена снизу.
– ограничена снизу. имеет предел
имеет предел 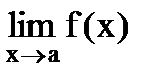 , то она ограничена в некоторой окрестности точки a.
, то она ограничена в некоторой окрестности точки a.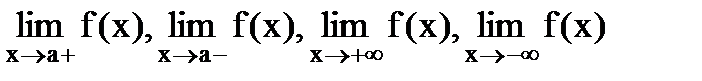 функция ограничена в соответствующих интервалах
функция ограничена в соответствующих интервалах
 называется неубывающей (возрастающей) в интервале
называется неубывающей (возрастающей) в интервале ), если для любых
), если для любых 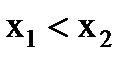 из этого интервала выполняется неравенство
из этого интервала выполняется неравенство (
(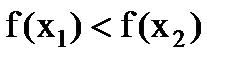 ).
). , имеет место
, имеет место (
( ),
), ). Такие функции называют монотонными на (а;
). Такие функции называют монотонными на (а;  ).
).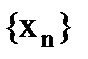 называется неубывающей (невозрастающей), если для любых
называется неубывающей (невозрастающей), если для любых  выполняется
выполняется .
. монотонна, убывает на интервале (-¥,0) и возрастает на интервале (0,+¥).
монотонна, убывает на интервале (-¥,0) и возрастает на интервале (0,+¥).
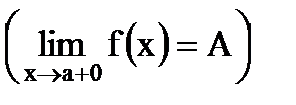 и
и  .
. .
.
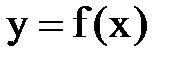
 и число
и число  , что
, что 
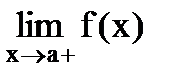 и
и  .
. , кроме этой точки, для функций
, кроме этой точки, для функций  выполняется соотношение
выполняется соотношение  и пусть пределы
и пусть пределы 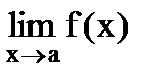 и
и  существуют и равны между собой,
существуют и равны между собой,  . Тогда
. Тогда  также существует и равен
также существует и равен  (см. рис 7).
(см. рис 7).