
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 8. Числове інтегрування звичайних диференційних рівнянь та систем диференційних рівнянь
Короткі теоретичні відомості Для ЗДР першого порядку задача Коші полягає в знаходженні такого розв’язку рівняння:
що задовольняє початкову умову
де Для диференціального рівняння m -го порядку
задача Коші полягає в знаходженні функції y = y (t), що задовольняє рівняння (8.3) і початкові умови:
Розв’язуючи деякі задачі, слід знайти m функцій y 1(t), y 2(t),…, ym (t), що задовольняють систему диференціальних рівнянь:
…
і початкові умови
Систему диференціальних рівнянь (8.4) називають нормальною. Задачу Коші (8.4) з початковими умовами (8.5) можна подати у векторній формі
де Систему диференціальних рівнянь
у якій Якщо ввести позначення
то систему лінійних диференціальних рівнянь записують у матричній формі:
Рівняння (8.3) за допомогою заміни змінних
можна звести до вигляду (8.6). Наприклад, рівняння
можна записати як систему
При чисельному розв’язку задачі Коші по змінній t вводять сітку 0< t 1< t 2<...< tn та шукають значення невідомої функції в вузлах сітки. Позначимо як y (t) — точний розв’язок задачі (8.1), (8.2), а yi +1 — наближений розв’язок в точці t = ti +1. Локальною похибкою розв’язку називають
При використанні наближених методів основним є питання про збіжність. Найбільше розповсюдження отримало поняття про збіжність при hi ®0, де hi = ti +1 – ti. Говорять, що метод збігається в точці ti +1, якщо Говорять, що метод має p -ий порядок точності, якщо існує таке число p >0, що
Метод Ейлера Для чисельного розв’язання задачі Коші (8.1), (8.2) розіб’ємо інтервал [0, tn ], на якому шукається розв’язок, на елементарні відрізки [ ti, ti +1],
тоді
Підставляючи (8.8) в (8.1) та замінюючи функцію f (t, y) її значенням на початку елементарного відрізку, отримаємо
В методі Ейлера рівняння (8.1) замінюється різницевим рівнянням (8.9). З (8.9) випливає, що наближений розв’язок задачі Коші знаходиться явно за рекурентною формулою
Оцінимо локальну похибку методу Ейлера. Для цього припустимо, що в точці t = ti значення функції y (t) обчислено точно, тобто y (ti)= yi. Розкладаючи функцію y (t) в ряд Тейлора в околі точки t = ti і враховуючи (8.1) отримаємо
Звідси
Враховуючи (8.10), вважаючи крок інтегрування hi малим та нехтуючи малими величинами вищих порядків із (8.7) та (8.11) отримуємо
Таким чином, метод Ейлера має перший порядок точності. Тому в методі Ейлера зменшення кроку hi в два рази в чотири рази зменшує локальну похибку розв’язку. Існують інші різновиди методу. Так, підставляючи (8.8) до (8.1) і замінюючи функцію f (t, y) її значення у кінці елементарного відрізку, отримаємо
Звідси
Для довільної функції f (t, y) значення yi +1 не може бути виражене з (8.12) явно. Тому метод (8.12) називають неявним методом Ейлера. При використанні неявного методу Ейлера нове значення yi +1 визначається на основі попереднього yi шляхом розв’язання нелінійного рівняння (8.12). Неявний метод Ейлера також має перший порядок точності. Можна показати, що похибка неявного методу Ейлера дорівнює
Наприклад: Нехай дано задачу Коші
Точним розв’язком цієї задачі є функція Необхідно обчислити таблицю значень y (t) на інтервалі Скористаємося явним методом Ейлера. Оскільки f (t, y)=- y 2(t +1), то згідно з формулою (8.10)
Тоді
Розв'яжемо цю ж задачу неявним методом Ейлера. Згідно з формулою (8.12) маємо
що приводить до рівняння відносно yi +1:
Тоді
Наприклад: Проінтегрувати систему ЗДР з початковими умовами
Розв’язання: Використовуючи метод Ейлера з кроком h= 0,1,обчислення будемо проводити з чотирма десятинними знаками:
Отже, занесемо значення до таблиці:
Відповідь: y=[0; 0,01; 0,0222; 0,038; 0,0576; 0,0828]; z=[1; 1,1; 1,221; 1,365; 1,535; 1,735].
Методи Рунге – Кутта У найзагальнішому випадку метод Рунге-Кутта порядку точності p будується за рекурентною формулою:
де
a 1=0, aj и cj – константи, bjl – елементи нижньотрикутної матриці, такої, що кожне kj отримується з попередніх значень kl. Формули (8.13) та (8.14) містять Як приклад розглянемо побудову методів Рунге-Кутта другого порядку точності (p =2). В цьому випадку можна отримати розв’язок для коефіцієнтів bjl, aj и cj при m =2. Тоді формула (8.13) перетвориться:
де Розкладемо k 1 і k 2 в ряд Тейлора в околі точки (ti, yi). Для цього відмітимо, що
тоді
Підставляючи (8.16) та (8.17) в (8.15), отримаємо
Розкладемо функцію y (t) в ряд Тейлора в околі точки (yi, ti) та знайдемо y (ti +1). Тоді
Врахуємо, що
Підставляючи (8.9) та (8.20) в (8.18), маємо
Для того, щоб метод мав другий порядок точності (
Рівняння (8.22) складають систему з 3 рівнянь відносно 4 невідомих. Виразимо b, c 1 и c 2 через a ¹0. Отримаємо:
Підставляючи (8.23) в (8.18) отримаємо такий узагальнений метод Рунге-Кутта другого порядку точності
де Широковідомим методом 2 порядку є окремий випадок методу (8.24) при
де Аналогічно будуються розрахункові формули методів Рунге-Кутта вищих порядків точності. При цьому відповідні системи рівнянь відносно bjl, aj та cj для p =2,3,4 можуть бути розв’язані відповідно для m =2,3,4. Таким чином, для того, щоб побудувати метод порядку точності p для p =2,3 та 4 достатньо m = p викликів функції f (t, y). Проте для p =5 ця система може бути розв’язана тільки при m ³6. Таким чином, для методу Рунге-Кутта 5 порядку точності потрібно щонайменше 6 викликів функції на кожному кроці. Аналогічно для p =6 m ³7. Це, зокрема, пояснює популярність класичного методу четвертого порядку, оскільки для того, щоб отримати додатковий порядок точності додатково потрібні два обчислення функції. Серед всього різноманіття методів Рунге-Кутта 4 порядку слід також відмітити найпоширенішу модифікацію методу з найбільш простим набором коефіцієнтів bjl, aj та cj:
Проте, слід зазначити, що використання формул (8.25) не дає змогу побудувати досить ефективні алгоритми розв’язку задачі Коші і його слід використовувати тільки для напів-аналітичних розрахунків або на початкових етапах розробки програмного забезпечення для отримання первинних оцінок. Наприклад:
t 0=0;
Методи Рунке-Кутта можуть бути застосовані також до розвязку систем ЗДР. При цьому розвязок системи ЗДР зводиться до розвязку на кожному кроці систем нелінійних рівнянь. Наприклад: Розв’язати попередню систему диференційних рівнянь методом Рунге-Кутта: Розв’язання: Так як
Отже,
таким же чином знайдемо y2(0,1) i z2(0,1) в точці x2(0,1)= 0,2; y2(0,1)= 0,0252; z2(0,1)= 1,2451
Обчислимо значення y(0,2) та z(0,2) в точці x1(0,2)= 0,2,але з кроком h= 0,2 y1(0,2)= 0,0253 z1(0,2)= 1,2453 Похибка значень y1(0,2) та z1(0,2) дорівнює:
Продовжуючи обчислення ми маємо:
Відповідь: y=[0; 0,011; 0,025; 0,044; 0,067; 0,097]; z=[1; 1,111; 1,245; 1,405; 1,595; 1,818]. Аналогічні схеми можна побудувати на основі методів більш високого порядку. Методи Ейлера та Рунге – Кутта називаються одноточковими. Це пояснюється тим, що для обчислення результату в
Багатоточкові методи В одноточкових методах значення В загальному випадку лінійним m -кроковим різницевим методом з постійним кроком називається система різницевих рівнянь:
де ak, bk — числові коефіцієнти, що не залежать від i, Метод називається лінійним, тому що кожне fk входить до формули лінійно. Рівняння (8.26) є рекурентним співвідношенням, за яким нове значення yi+ 1 виражається через раніше знайдені yi, yi- 1, yi- 2,..., yi-m+ 1. Обчислення починається з i = m– 1, тобто з рівняння
Звідси видно, що для початку обчислень слід задати m початкових значень y 0, y 1,... ym -1. Значення y 0 задається умовою (8.26). Величини y 1, y 2,... ym -1 можна обчислити використовуючи однокрокові методи, наприклад, методи Рунге-Кутта. Метод (8.26) називається явним, якщо b 0=0, і, відповідно, шукане значення yi +1 виражається через попередні yi, yi-1,..., yi-m +1
Якщо b 0¹0, то метод називається неявним. Тоді для знаходження yi +1 доводиться розв’язувати нелінійне рівняння
Зазвичай це рівняння розв’язують методом Ньютона і задають початкове наближення yi +1(0), що дорівнює yi. Слід відзначити, що коефіцієнти рівняння (8.26) задані з точністю до множника. Щоб усунути цю неоднозначність, вимагають виконання умови нормування
Можна показати, що для того, аби різницевий метод (8.26) мав порядок точності p, необхідно щоб були виконані умови:
Разом з умовою нормування (8.29) рівняння (8.30) і (8.31) становлять систему з p +2 лінійних алгебраїчних рівнянь відносно 2 m +2 невідомих Для того, щоб існував розв’язок цієї системи, необхідно, щоб кількість рівнянь була не більшою від кількості невідомих, тому p £2 m. Ця вимога означає, що лінійні m -крокові різницеві методі мають порядок точності не більше, ніж 2 m. Тому порядок точності неявних m -крокових методів дорівнює 2 m, коли ai ¹0, bi ¹0,
У практиці обчислень найбільше поширення отримали методи Адамса, які становлять частковий випадок багатокрокових методів (8.26), коли похідна y ¢ апроксимується тільки по двох точках ti +1, ti, тобто
Таким чином, методи Адамса мають вигляд
У випадку b 0=0 методи Адамса називають явними, а при b 0¹0 — неявними. Для методів Адамса умови (8.29), (8.31) приймають вигляд
Звідси видно, що найвищий порядок точності m -крокового неявного методу Адамса дорівнює m +1 (кількість рівнянь р, а невідомих — m +1), а найвищий порядок точності явного методу дорівнює m (b 0=0). Знайдемо коефіцієнти bk для кількох m. Розглянемо явні методи Адамса. Коефіцієнти знаходять із (10.33), (10.34) при p = m. При m =1 отримуємо метод Ейлера
При m =2 (10.33) приймає вигляд
Звідси Таким чином, при m =2, отримаємо явний метод Адамса другого порядку
Звідси
Розв’язки для інших m наведено у таблиці 8.1. Коефіцієнти неявного методу Адамса знаходяться із системи (8.33), (8.34) з р = m +1. Наведемо формули неявних
Таблиця 8.1. Коефіцієнти явного методу Адамса порядку m
Для
Наприклад: Нехай дано задачу Коші
Необхідно обчислити таблицю значень y (t) на інтервалі Застосуємо трьохточковий явний метод Адамса. Використовуючи таблицю 8.1 отримаємо загальну формулу для цього методу:
Спочатку обчислимо значення
Після цього продовжимо розв’язок заданим методом:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.32 (0.127 с.) |
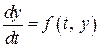 , (8.1)
, (8.1)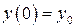 , (8.2)
, (8.2)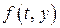 – задана неперервна функція двох аргументів,
– задана неперервна функція двох аргументів, 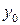 – задана константа.
– задана константа. (8.3)
(8.3)

 (8.4)
(8.4)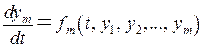
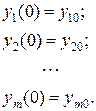 (8.5)
(8.5) (8.6)
(8.6)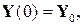
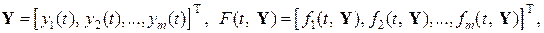

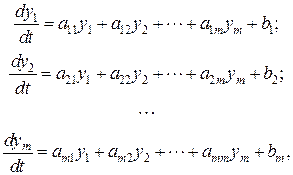
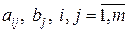 – функції від t, називають лінійною.
– функції від t, називають лінійною.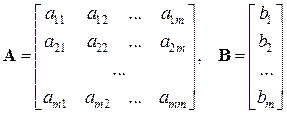 ,
, .
.

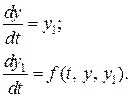
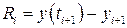 (8.7)
(8.7) . Метод збігається на відрізку [0, tn ], якщо він збігається в кожній точці t Î[0, tn ].
. Метод збігається на відрізку [0, tn ], якщо він збігається в кожній точці t Î[0, tn ].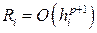 , при hi ®0.
, при hi ®0.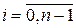 , t 0=0. На кожному елементарному відрізку будемо шукати розв’язок у вигляді полінома першого ступеня. Нехай значення функції на границях елементарного відрізку становить yi, yi+ 1. За інтерполяційною формулою Лагранжа
, t 0=0. На кожному елементарному відрізку будемо шукати розв’язок у вигляді полінома першого ступеня. Нехай значення функції на границях елементарного відрізку становить yi, yi+ 1. За інтерполяційною формулою Лагранжа .
.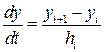 . (8.8)
. (8.8)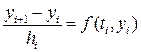 . (8.9)
. (8.9)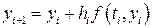 (8.10)
(8.10)
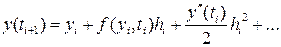 (8.11)
(8.11) .
.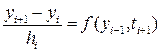 .
.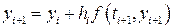 . (8.12)
. (8.12) .
. .
. .
. з кроком h =0,25, тобто для t 0=0, t 1=0,25, t 2=0,5, t 3=0,75, t 4=1.
з кроком h =0,25, тобто для t 0=0, t 1=0,25, t 2=0,5, t 3=0,75, t 4=1. .
.
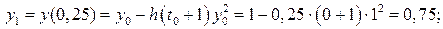
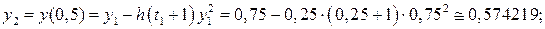
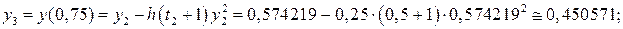
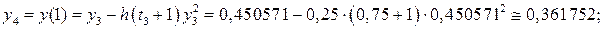
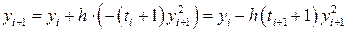 ,
, .
. ;
;
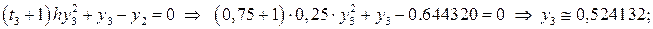

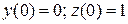 на відрізку (0; 0,5) з точністю до 10-3
на відрізку (0; 0,5) з точністю до 10-3
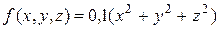 ,
,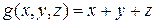

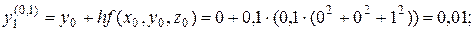

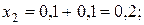
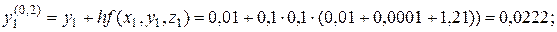
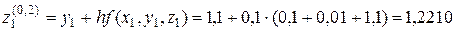 і т.д.
і т.д.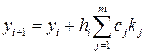 , (8.13)
, (8.13) , (8.14)
, (8.14)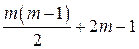 коефіцієнтів bjl, aj та c, що підлягають визначенню. Для того, щоб знайти ці коефіцієнти всі функції kj розкладають в ряд Тейлора в околі точки (ti, yi). Ці розклади підставляють в (8.13) і результат зрівнюють з рядом Тейлора для функції y (ti +1). Оскільки локальна похибка визначена згідно з (8.7), то ставиться умова, щоб коефіцієнти при всіх
коефіцієнтів bjl, aj та c, що підлягають визначенню. Для того, щоб знайти ці коефіцієнти всі функції kj розкладають в ряд Тейлора в околі точки (ti, yi). Ці розклади підставляють в (8.13) і результат зрівнюють з рядом Тейлора для функції y (ti +1). Оскільки локальна похибка визначена згідно з (8.7), то ставиться умова, щоб коефіцієнти при всіх 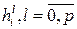 в розкладах для y (ti +1) и yi +1 були рівні. Ця вимога приводить до системи рівнянь відносно коефіцієнтів bjl, aj и cj.
в розкладах для y (ti +1) и yi +1 були рівні. Ця вимога приводить до системи рівнянь відносно коефіцієнтів bjl, aj и cj. , (8.15)
, (8.15)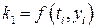 ,
, 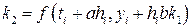 .
. .
. (8.17)
(8.17)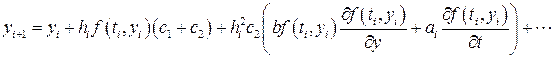 .
.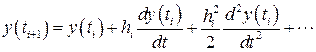 . (8.18)
. (8.18)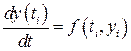 , (8.19)
, (8.19)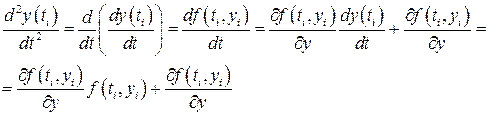 (8.20)
(8.20) (8.21)
(8.21) ), вимагатимемо, щоб в різниці рівнянь (8.18) та (8.21) були відсутні доданки, які містять
), вимагатимемо, щоб в різниці рівнянь (8.18) та (8.21) були відсутні доданки, які містять  ,
,  и
и 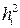 . Виходячи з цієї умови коефіцієнти a, b, c 1 и c 2 повинні задовольняти системі рівнянь:
. Виходячи з цієї умови коефіцієнти a, b, c 1 и c 2 повинні задовольняти системі рівнянь: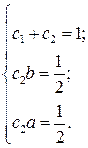 (8.22)
(8.22)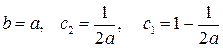 . (8.23)
. (8.23)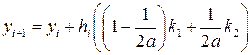 , (8.24)
, (8.24)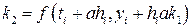 .
. :
: ,
, .
. (8.25)
(8.25)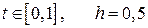 .
.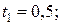
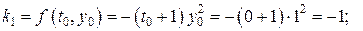

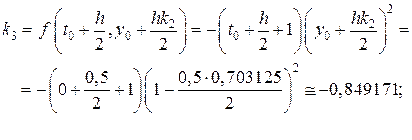
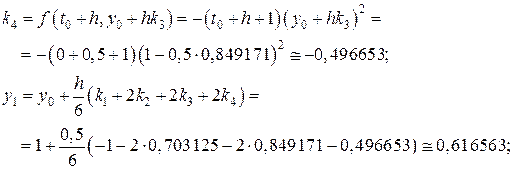
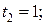
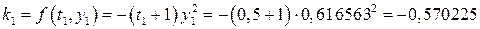 ;
;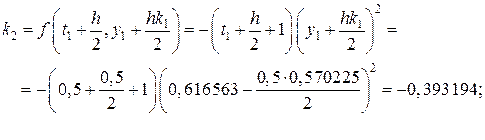

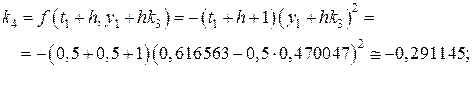
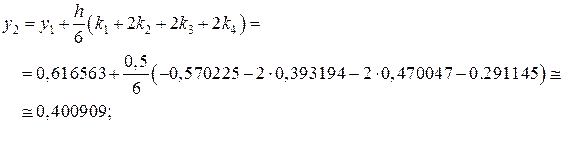
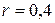 , знаходимо
, знаходимо 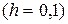 :
:
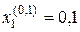
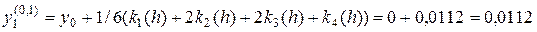 ;
;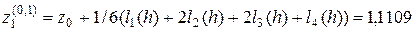 ;
;
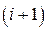 -й точці достатньо знати значення лише в одній попередній i -й точці.
-й точці достатньо знати значення лише в одній попередній i -й точці.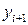 обчислюють на основі значення в одній попередній точці
обчислюють на основі значення в одній попередній точці 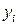 . При цьому логічно припустити, що можна підвищити точність, якщо в розрахунку значення в точці
. При цьому логічно припустити, що можна підвищити точність, якщо в розрахунку значення в точці 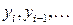
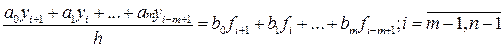 ; (8.26)
; (8.26)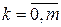 , причому a 0¹0, fk = f (tk, yk), h = ti +1- ti,
, причому a 0¹0, fk = f (tk, yk), h = ti +1- ti,  .
.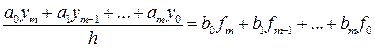 .
.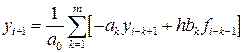 (8.27)
(8.27)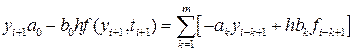 . (8.28)
. (8.28)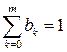 . (8.29)
. (8.29)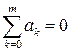 ; (8.30)
; (8.30)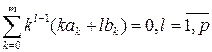 . (8.31)
. (8.31) .
. , а явних — 2 m -1, оскільки b 0=0 і невідомих в (8.29), (8.30), (8.31) на одну менше.
, а явних — 2 m -1, оскільки b 0=0 і невідомих в (8.29), (8.30), (8.31) на одну менше.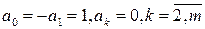 .
.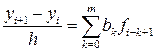 . (8.32)
. (8.32)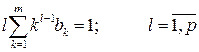 ; (8.33)
; (8.33)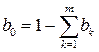 . (10.34)
. (10.34)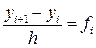 .
.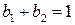 ;
; .
.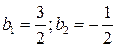 .
.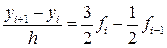 .
.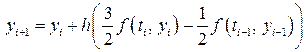 .
. -точкових методів Адамса для деяких значень m:
-точкових методів Адамса для деяких значень m: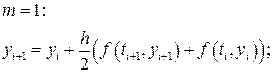

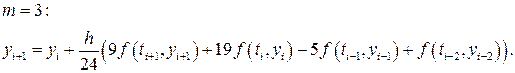
 обчислювальна схема матиме вигляд:
обчислювальна схема матиме вигляд:
 .
. явним методом Ейлера:
явним методом Ейлера: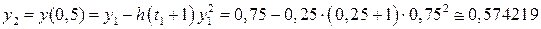 .
.



