
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполяційні формули НьютонаСтр 1 из 7Следующая ⇒
Формула Ньютона дає змогу виразити інтерполяційний поліном Pn (x) через значення yi в одному з вузлів та через розділені різниці функції f (x), побудованими за іншими вузлами x 0, x 1,…, xn. Вона є аналогом формули Тейлора. Розділеними різницями першого порядку називають відношення
Розглянемо розділені різниці, побудовані за сусідніми вузлами, тобто вирази
Аналогічно:
Скориставшись цим виразом, записуємо інтерполяційну формулу
Позначивши
Формулу (7.10) називається формулою Ньютона інтерполювання вперед, оскільки формула містить значення y, що знаходяться справа від x 1. Аналогічним чином можна побудувати формулу Ньютона використовуючи вузли, що знаходяться зліва від xn:
Позначивши
Формула (7.12) називають другою інтерполяційною формулою Ньютона. Її зручно використовувати для інтерполяції функції у точках, близьких до кінця таблиці. Залишковий член першої інтерполяційної формули Ньютона:
де Оцінка абсолютної похибки функції визначається за формулою:
де Для другої інтерполяційної формули Ньютона залишковий член має вигляд:
а абсолютна похибка функції дорівнює:
де
Наприклад: В таблиці 7.2 всі значення функції Розв’язання. В даному прикладі шаг інтерполяції постійний
Похибку результату оцінюємо за формулою (7.14). Оскільки
Інтерполяція сплайнами Нехай функцію задано табл. 7.3 і треба побудувати сплайн-інтерполяцію цієї функції.
Таблиця 7.3.
За допомогою сплайнів функцію можна подати у вигляді
Для побудови сплайн-інтерполяції визначають невідомі коефіцієнти a01, a02,…amn. Якщо функція інтерполюється на n інтервалах за допомогою поліномів порядку m, то кількість таких невідомих буде (m + 1)n. Для їх визначення потрібно (m + 1)n рівнянь. Щоб отримати необхідну кількість рівнянь, можна скористатися умовами рівності функції табличним значенням у вузлах інтерполяції. Ці умови дадуть 2n рівнянь, чого вистачить для інтерполяції сплайнами першого порядку (лінійними сплайнами, m = 1). Для інтерполяції сплайнами другого порядку (параболічними сплайнами, m = 2) ці рівняння необхідно доповнити умовою неперервності першої похідної. Це дасть ще (n – 1) рівняння. Отриману систему треба доповнити ще одним рівнянням. Наприклад, можна задати поведінку функції на одному з кінців інтервалу (наприклад, рівність Останнє рівняння отримують, задавши поведінку функції на другому (незадіяному) кінці відрізка. На практиці часто задають однакові умови на кінцях інтервалу. Як правило, це умова гладкості функції на кінцях ( Наприклад: Проведемо кубічну інтерполяцію функції, заданої в табл. 7.2. На кожному і -му відрізку:
Побудуємо систему рівнянь для визначення невідомих коефіцієнтів. З умови рівності функції табличним значенням у вузлових точках маємо:
З умови неперервності першої та другої похідних функцій:
З умови гладкості функції:
Розв’язавши рівняння (7.17) –(7.19), отримаємо:
Тоді функція має вигляд
Контрольні завдання 1. Вибрати табличну функцію відповідно до свого варіанта. 2. Побудувати інтерполяційний поліном Лагранжа для заданої функції. 3. Побудувати інтерполяційний поліном Ньютона для заданої функції. 4. Побудувати кубічну інтерполяційну формулу заданої функції.
5. Побудувати графіки, нанести на них точки таблиці та порівняти отримані результати. Варіанти завдань
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.214 (0.081 с.) |
 .
.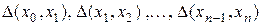 . За цими розділеними різницями можна побудувати різниці другого порядку, за різницями другого порядку – різниці третього порядку і т. д:
. За цими розділеними різницями можна побудувати різниці другого порядку, за різницями другого порядку – різниці третього порядку і т. д: Розглянемо розділену різницю
Розглянемо розділену різницю  . Звідси знаходимо
. Звідси знаходимо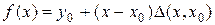 .
.
 .
. (7.9)
(7.9) ;
;  ;
;  ;
;  ;
;  тоді формула (7.9) набуває вигляду
тоді формула (7.9) набуває вигляду (7.10)
(7.10) - перша інтерполяційна формула Ньютона.
- перша інтерполяційна формула Ньютона.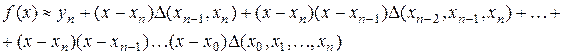 (7.11)
(7.11)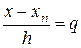 , дістанемо
, дістанемо  ;
;  ;
;  тоді формула (7.11) набуває вигляду:
тоді формула (7.11) набуває вигляду: (7.12)
(7.12) , (7.13)
, (7.13)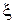 - деяке проміжне значення між вузлами інтерполяції
- деяке проміжне значення між вузлами інтерполяції 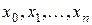 і розглянутою точкою
і розглянутою точкою  .
. , (7.14)
, (7.14) .
. , (7.15)
, (7.15) , (7.16)
, (7.16)


 наведені з правильними значущими цифрами. Потрібно обчислити значення
наведені з правильними значущими цифрами. Потрібно обчислити значення  , та оцінити похибку результату. Таблиця 7.2.
, та оцінити похибку результату. Таблиця 7.2. . Значення
. Значення  знаходиться ближче до початку таблиці, отже будемо користуватися першою формулою Ньютона. Позначимо
знаходиться ближче до початку таблиці, отже будемо користуватися першою формулою Ньютона. Позначимо  . Користуючись формулою (7.10) маємо:
. Користуючись формулою (7.10) маємо: , де
, де  . Підставивши значення
. Підставивши значення  отримаємо
отримаємо 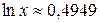 .
. для всіх
для всіх 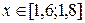 , то візьмемо
, то візьмемо  , тоді:
, тоді: .
.






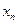

 причому похідна функції обчислюється числовим методом на основі табличних значень функції). У разі інтерполяції кубічними сплайнами систему рівнянь необхідно доповнити ще n рівняннями. Для цього можна поставити вимогу неперервності другої похідної функції, що дасть (n – 1) рівняння.
причому похідна функції обчислюється числовим методом на основі табличних значень функції). У разі інтерполяції кубічними сплайнами систему рівнянь необхідно доповнити ще n рівняннями. Для цього можна поставити вимогу неперервності другої похідної функції, що дасть (n – 1) рівняння.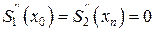 ).
). ,
,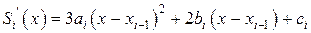 ,
,  .
. (7.17)
(7.17)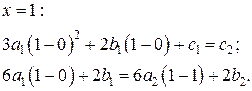 (7.18)
(7.18) (7.19)
(7.19)




