
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення крайових задач до задач Коші
Подамо крайову задачу із виразів (8.46) і (8.47) для диференціального рівняння m- го порядку у вигляді:
де L – диференціальний оператор, а a ij, b ij, g j – сталі. Задачу (8.48), з умовою (8.49) найпростіше звести до задачі Коші, якщо L – лінійний диференціальний оператор
У цьому випадку розв’язок шукають у вигляді
де zk (x) знаходять з (m + 1) задачі Коші
Після розв’язання задач Коші (8.51) на відрізку [0, l ], вираз (8.52) підставляють у вираз (8.49) і одержують СЛАР з m рівнянь відносно m невідомих ck, Наприклад:
Шукаємо розв’язок у вигляді
де Із розв’язків задач Коші на відрізку [0, 1]
отримуємо З першої крайової умови маємо
З другої умови:
Якщо L – нелінійний диференціальний оператор, то для зведення крайової задачі до задачі Коші застосовують метод «стрільби». Для цього розв’язок y (x) шукають у вигляді y = z (x), де z (x) – розв’язок задачі Коші
Значення zi у початковій умові (8.52) підбирають такими, щоб задовольнити (8.49). У цьому випадку крайові умови (8.49) разом з (8.49) і (8.53) утворюють систему m нелінійних рівнянь щодо m невідомих Наприклад: Припустимо, що потрібно розв’язати задачу
за умов:
Можна застосувати такий ітераційний метод: 1) вибирати x, що апроксимує
2) розв’язати задачу Коші:
3) якщо
Метод скінчених різниць Поширеним методом розв’язання крайових задач є метод скінчених різниць (МСР). В основі МСР лежить апроксимація похідних в операторі L (8.48) і в крайових умовах (8.49) скінченими різницями, а неперервної функції f (x) – сітковою функцією, визначеною у вузлах відрізка [0, l ]. Розглянемо найпростіший випадок, коли вузли сіткової функції – рівновіддалені. Для цього відрізок [0, l ] ділять на n ³ m +1 рівних відрізків вузлами x 0 = 0, x 1 = x 0 + h, x 2 = x 0 + 2 h,…, xn = x 0 + nh. Розв’язання задачі (8.48) за (8.49) зводиться до визначення значень функцій у вузлах yi = y (xi).
Один зі способів різницевої апроксимації похідних побудований на диференціюванні інтерполяційних формул. Так, для одержання скінченнорізницевої апроксимації похідної Тоді Похибка такої апроксимації оцінюється як де
Як приклад знайдемо скінчено різницеву апроксимацію першої і другої похідних функції y (x) у точці x = xi, побудовану в трьох точках. Побудуємо поліном Лагранжа, що проходить через точки (xi -1, yi- 1), (xi, yi), (xi+ 1, yi+ 1):
Тоді
Похибкою цих апроксимацій є 0(h 2). У методі скінчених різниць диференціальне рівняння (8.48) заміняється скінчено різницевими рівняннями, записаними для n – m + 1 внутрішнього вузла відрізка [0, l ]. Граничні умови (8.49) заміняються m скінчено різницевими рівняннями. У підсумку одержуємо СЛАР з n + 1 рівняння відносно n + 1 невідомих Наприклад:
Точний розв’язок:
Поділимо відрізок [0, 1] на три рівні відрізки. Тоді Шукаємо Використовуючи скінчено різницеву апроксимацію
З крайових умов:
Одержимо систему чотирьох рівнянь стосовно чотирьох невідомих
Контрольні завдання 1. Вибрати задачі Коші відповідно до свого варіанта. 2. Розв’язати одновимірну задачу Коші методом Ейлера з похибкою не більше 5 %. 3. Розв’язати одновимірну задачу Коші методом Рунге – Кутта 4-го порядку з похибкою не більше 5 %. 4. Розв’язати одновимірну задачу Коші явним методом Адамса 4-го порядку з похибкою не більше 5 %. 5. Розв’язати одновимірну задачу Коші методом Гіра 4-го порядку з похибкою не більше 5 %. 6. Порівняти результати пп. 1 – 5. 7. Розв’язати систему ЗДР методом Ейлера. Оцінити похибку розв’язку. Варіанти завдань
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.228 (0.013 с.) |
 ; (8.48)
; (8.48) , (8.49)
, (8.49)
 , (8.50)
, (8.50) (8.51)
(8.51)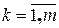 . Розв’язавши СЛАР з (8.50), знаходять розв’язок задач (8.48) з умовою (8.49).
. Розв’язавши СЛАР з (8.50), знаходять розв’язок задач (8.48) з умовою (8.49).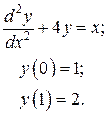
 ,
, – розв’язок неоднорідної задачі Коші з нульовими початковими умовами, а
– розв’язок неоднорідної задачі Коші з нульовими початковими умовами, а  – розв’язки однорідних задач Коші з ненульовими початковими умовами відповідно до (8.51).
– розв’язки однорідних задач Коші з ненульовими початковими умовами відповідно до (8.51).
 . Далі знаходимо сталі c 1 та c 2.
. Далі знаходимо сталі c 1 та c 2. .
. .
.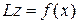 ; (8.52)
; (8.52) (8.53)
(8.53) . Останній розв’язок (8.52) і є розв’язком задачі (8.48) з умови (8.49).
. Останній розв’язок (8.52) і є розв’язком задачі (8.48) з умови (8.49).

 , тобто покласти
, тобто покласти

 , де e – задана похибка, то покласти
, де e – задана похибка, то покласти  у противному випадку – змінити x (виконати ітерацію розв’язку нелінійного рівняння) і повернутися до пункту 2).
у противному випадку – змінити x (виконати ітерацію розв’язку нелінійного рівняння) і повернутися до пункту 2). будуємо інтерполяційний поліном Лагранжа
будуємо інтерполяційний поліном Лагранжа 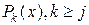 , який проходить через k + 1 точку
, який проходить через k + 1 точку 
 …,
…, 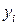 ,…,
,…, 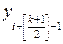 ,
,  .
.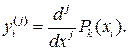
 ,
,
 .
. ;
; .
. . Похибка розв’язку методом скінчених різниць відповідає найбільшій похибці апроксимації похідних у (8.48), (8.49).
. Похибка розв’язку методом скінчених різниць відповідає найбільшій похибці апроксимації похідних у (8.48), (8.49).
 .
.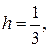
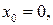
 .
.
 , запишемо скінчено різницеве рівняння для вузлів
, запишемо скінчено різницеве рівняння для вузлів  :
:
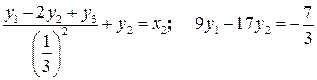 .
.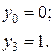
 . Розв’язуючи її, одержимо:
. Розв’язуючи її, одержимо:



