
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апостеріорна оцінка похибки розв’язання задачі Коші. Автоматичний вибір кроку інтегрування.
При чисельному розв’язанні задачі Коші використовують різні методи апостеріорної оцінки похибки в залежності від обраного методу та інших факторів. Найбільш широко застосовується правило Рунге:
де Наприклад: Нехай дано задачу Коші
Необхідно обчислити значення y (t) в точці t =1 та оцінити похибку результату. Скористаємося явним методом Ейлера. Виберемо крок h =0,5. Тоді
Для того, щоб скористатись правилом Рунге (8.35) необхідно обчислення виконати ще раз, але з кроком вдвічі меншим (q =2), тобто h =0,25. Результатом є
Точним розв’язком цієї задачі Коші є функція При розв’язанні задачі Коші неявними методами використання правила Рунге є неефективним, оскільки при зменшенні кроку доводиться додатково розв’язувати q нелінійних рівнянь. Тому при використанні неявних методів застосовують інші методи оцінки похибки. Так, наприклад, при порівнянні формул для похибок явного та неявного методів Ейлера видно, що при h ®0 модулі цих похибок є однаковими, але вони мають протилежний знак. Ця особливість дає змогу апостеріорно оцінити похибку неявного методу за формулою:
де Наприклад: Для вищенаведеної задачі Коші треба оцінити похибку неявного методу Ейлера точці t =1 при розв’язанні задачі з кроком h =0,25, маємо
Як видно ця оцінка близька до дійсної похибки. При застосуванні методів Рунге-Кутта використовують інший підхід. В ньому оцінка похибки розраховується як різниця результатів отриманих методами з різними порядками точності:
де yi +1– розв’язок, отриманий методом з порядком точності p, а
Існують і інші підходи для оцінки похибки розв’язання задачі Коші. Так, наприклад, можна оцінити похідну, яка входить в формулу похибки. Для явного методу Ейлера досить оцінити
Інший спосіб оцінки похідної ґрунтується на диференціюванні інтерполяційних поліномів. Так, наприклад, для оцінки Наявність методів оцінки похибки на кожному кроці дає можливість підбирати крок інтегрування залежно від необхідної точності розв’язку. Для цього після знаходження оцінки похибки Ri перевіряють виконання умови:
де e – задана відносна похибка розв’язку. Якщо умова (8.38) не виконується, то крок зменшують в q разів або в Крок на наступному інтервалі вибирають за формулою:
або за правилом зон:
Якщо необхідно обчислити значення функції в наперед заданих вузлах, можна використовувати метод екстраполяції нульового кроку. Для цього на кожному елементарному відрізку знаходять значення yi +1 з різними кроками, які, як правило, відрізняються один від одного в два рази. На j ‑му етапі екстраполяції будують послідовність розв’язків за формулами:
Крок послідовно зменшують доти, доки нова екстраполяція не буде відрізнятися від попередньої не більше, ніж на задану величину похибки розв’язку. При цьому остання екстраполяція є екстраполяцією нульового кроку. В цьому методі автоматичний вибір кроку не потрібний. Жорсткі рівняння Поняття жорсткого рівняння пов’язано з жорсткою умовою стійкості для різницевих схем розв’язання цих рівнянь. Розглянемо задачу Коші:
де l – досить велике від’ємне число. Точний розв’язок задачі (8.39) має вигляд
Із виразу (8.40) випливає, що для любого ti і hi > 0:
Застосуємо для розв’язання задачі (8.39) явний метод Ейлера:
Із виразу (8.42) випливає, що умова (8.41) виконується, якщо
Отже, процес (8.42) буде стійким для виконання співвідношення (8.41) тільки за умови, що
За великих значень l крок інтегрування жорстко обмежують і вибирають, виходячи не стільки з умови забезпечення заданої похибки розв’язку, а так, щоб задовольнити вираз (8.43). Для кількісної оцінки жорсткості рівняння вводять коефіцієнт жорсткості S. Коефіцієнт жорсткості для задачі (8.39) залежить не тільки від S =ïlï tn, де tn – права границя інтервалу інтегрування. Для системи диференціальних рівнянь жорсткість можна оцінити як
де l i — власні числа матриці Якобі системи диференціальних рівнянь. Обмеження (8.43) під час використання явних методів призводить до великих обчислювальних затрат через малий крок інтегрування, тому загальним підходом до розв’язання жорстких задач є використання неявних схем. Незважаючи на потребу розв’язання систем нелінійних рівнянь, за рахунок можливості значного збільшення кроку інтегрування загальний обсяг обчислень може бути значно меншим, ніж для явних методів. На сьогодні часто використовують метод Гіра у вигляді неявної схеми:
яка є окремим випадком багатоточкового методу (8.26) при
Для метода (8.44), який має порядок точності p = m, сталі Таблиця 8.2. Коефіцієнти методу Гіра порядку m
Наприклад. Нехай дано задачу Коші
Необхідно обчислити таблицю значень y (t) на інтервалі Використовуючи таблицю 8.2 отримаємо з (8.44) загальну формулу для цього методу:
Спочатку обчислимо значення
Після цього продовжимо розв’язок заданим методом:
Крайові задачі Часто фізичні задачі зводять до диференціального рівняння
де
де a ij, b ij, g j – сталі. Наприклад, для диференціального рівняння 2-го порядку задають умови на кінцях Аналогічно поставлено крайову задачу для системи диференціальних рівнянь. Методи розв’язання крайових задач відрізняються від методів розв’язання задачі Коші і поділені на два загальних класи – методи зведення крайових задач до задач Коші та спеціальні методи, призначені для розв’язання власне крайових задач.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.123 (0.019 с.) |
 , (8.35)
, (8.35)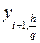 та
та  розв’язки задачі Коші в точці t = ti +1, отримані відповідно з кроками
розв’язки задачі Коші в точці t = ti +1, отримані відповідно з кроками  та h, q – ціле число, як правило рівне 2, p – порядок точності методу, що використовується, Ri – апостеріорна оцінка похибки для результату, отриманого з кроком
та h, q – ціле число, як правило рівне 2, p – порядок точності методу, що використовується, Ri – апостеріорна оцінка похибки для результату, отриманого з кроком  .
.

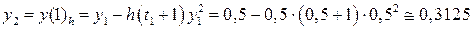 .
. . Тоді, враховуючи, що метод Ейлера має перший порядок точності (p =1) з формули (8.35) маємо
. Тоді, враховуючи, що метод Ейлера має перший порядок точності (p =1) з формули (8.35) маємо .
. . Тому точним розв’язком в точці t =1 є y (1)=0,4. Як видно отримана апостеріорна оцінка похибки обчислення
. Тому точним розв’язком в точці t =1 є y (1)=0,4. Як видно отримана апостеріорна оцінка похибки обчислення  є досить близькою до дійсної. Слід відзначити, що апостеріорна оцінка похибки тим ближча до дійсної, чим менший крок h.
є досить близькою до дійсної. Слід відзначити, що апостеріорна оцінка похибки тим ближча до дійсної, чим менший крок h. (8.36)
(8.36) та yi +1 – розв’язки отримані відповідно явним та неявним методом.
та yi +1 – розв’язки отримані відповідно явним та неявним методом. =0,361752 а y 4=0,431175. Тоді
=0,361752 а y 4=0,431175. Тоді .
.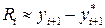 , (8.37)
, (8.37) ‑ з порядком точності p +1. Існує цілий ряд методів Рунге Кутта, коли для одних й тих самих функцій kj можна на наборі коефіцієнтів cj в (8.13) отримати метод 4 порядку точності, а на наборі
‑ з порядком точності p +1. Існує цілий ряд методів Рунге Кутта, коли для одних й тих самих функцій kj можна на наборі коефіцієнтів cj в (8.13) отримати метод 4 порядку точності, а на наборі  ‑ 5 порядок точності. Тому використання (8.37) практично не приводить до додаткових витрат а похибка оцінюється за формулою:
‑ 5 порядок точності. Тому використання (8.37) практично не приводить до додаткових витрат а похибка оцінюється за формулою: .
. . Для цього можна скористатися апроксимацією похідної функції f (t, y) скінченими різницями:
. Для цього можна скористатися апроксимацією похідної функції f (t, y) скінченими різницями: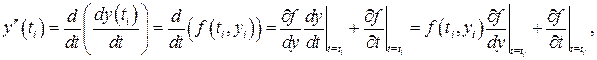 де
де  ,
,  ,
, 
 .
. , (8.38)
, (8.38) раз. Зменшення кроку виконують до тих пір, поки не виконається умова (10.38). Після цього переходять до наступного елементарного відрізку.
раз. Зменшення кроку виконують до тих пір, поки не виконається умова (10.38). Після цього переходять до наступного елементарного відрізку.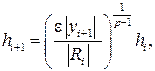

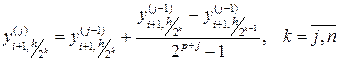 .
. (8.39)
(8.39) . (8.40)
. (8.40) . (8.41)
. (8.41) . (8.42)
. (8.42) .
. . (8.43)
. (8.43) , але й від довжини інтервалу інтегрування:
, але й від довжини інтервалу інтегрування: ,
, , (8.44)
, (8.44) . (8.45)
. (8.45) можуть бути знайдені з системи рівнянь (8.29), (8.31) з урахуванням
можуть бути знайдені з системи рівнянь (8.29), (8.31) з урахуванням 
 методом Гіра 3 порядку, якщо h =0,25.
методом Гіра 3 порядку, якщо h =0,25. .
. неявним методом Ейлера:
неявним методом Ейлера: ;
;


 -го порядку
-го порядку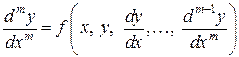 , (8.46)
, (8.46) – деяка фізична величина, визначена на відрізку
– деяка фізична величина, визначена на відрізку  , що описує певний процес. Часто відома поведінка процесу на кінцях відрізка
, що описує певний процес. Часто відома поведінка процесу на кінцях відрізка  (8.47)
(8.47) . Таку задачу називають крайовою задачею першого класу або задачею із закріпленими кінцями.
. Таку задачу називають крайовою задачею першого класу або задачею із закріпленими кінцями.


