
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 9. Числове розв’язання задач оптимізації
Короткі теоретичні відомості
Нехай функція f (x 1, x 2,..., xn) — неперервно диференційована в області D. Нехай відомо, що в D існує точка
Розв’язання системи (9.1) дозволяє визначити невідомі характеристичні точки. Потім, використовуючи достатні умови мінімуму, варто виділити ті точки області D, у яких досягається локальний мінімум. Порівнявши значення цільової функції в точках локального мінімуму, треба вибрати точку з мінімальним значенням локального мінімуму, тобто визначити глобальний мінімум f (x 1, x 2,..., xn) у області D. Однак надійні й одночасно економні методи пошуку глобального мінімуму на цей час невідомі. Необхідну умову екстремуму (9.1) – умову стаціонарності можна записати у вигляді
де Слід відзначити, що на відміну від нелінійних рівнянь f (x) = 0, які можна розв’язати з точністю e, задачу
Методи одновимірного пошуку Нехай f (x) – дійсна функція одного аргументу, визначена на відрізку [ a, b ]. Припустимо, що існує єдине значення c, таке, що f (c) – мінімум f (x) на відрізку [ a, b ], і що f (x) строго спадає для x < c і строго зростає для x > c. Така функція називається унімодальною. Метод золотого перерізу полягає в розбитті інтервалу [ a, b ] точкою x 1 на дві частини таким чином, щоб відношення довжини всього інтервалу до більшої частини дорівнювало відношенню більшої частини до меншої:
Легко перевірити, що золотий переріз утворюють дві точки x 1 = a + (1 – d)(b – a); x 2 = a + d(b – a), де Точка x 1 утворює золотий переріз відрізка [ a, x 2], а точка x 2 – інтервалу [ x 1, b ]. Тому на інтервалі, що залишився, потрібно визначити тільки одну точку, що утворює золотий переріз. На кожному кроці довжина першого інтервалу невизначеності дорівнює приблизно 0,618 довжини попереднього інтервалу. Алгоритм методу золотого перерізу: 1. Обчислити: x 1 := a + (1 – d)(b – a); x 2 := a + d(b – a). 2. Обчислити f(x1), f(x2). 3. Якщо f (x 1) < f (x 2), то покласти b:= x 2, x 2 := x 1, f (x 2):= f (x 1), 4. Якщо Наприклад: Знайти мінімум цільової функції Легко бачити, що точним розв’язком цієї задачі оптимізації є точка x =1.
Оберемо інтервал пошуку x Î[0,3], тобто a = 0, b = 3. Обчислимо x 1 та x 2.
Знайдемо значення цільової функції в точках x 1 та x 2.
Оскільки Для нового інтервалу значення x 2 та
Обчислимо нове значення x 1 та
Оскільки
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.147.4 (0.004 с.) |
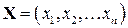 , в якій виконуються співвідношення:
, в якій виконуються співвідношення: (9.1)
(9.1)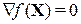 ,
, – градієнт цільової функції в точці
– градієнт цільової функції в точці  .
.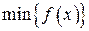 можна тільки з точністю
можна тільки з точністю  .
.
 .
.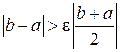 , то перейти до кроку 3, інакше
, то перейти до кроку 3, інакше  .
. методом золотого перерізу.
методом золотого перерізу.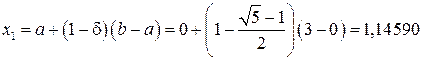 ;
; .
.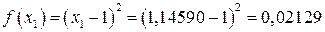 ,
,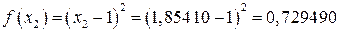 .
. , то
, то 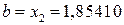 . Таким чином інтервал пошуку звузився до x Î[0, 1,85410].
. Таким чином інтервал пошуку звузився до x Î[0, 1,85410].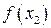 обчислювати не треба. Їх можна взяти з попередньої ітерації:
обчислювати не треба. Їх можна взяти з попередньої ітерації: ,
, 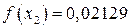 .
.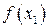 :
: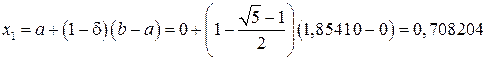 ;
;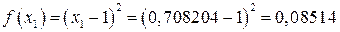 .
.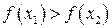 , то
, то  . Тобто інтервал пошуку звузився до x Î[0,708204, 1,85410]. Таким чином з кожною ітерацією інтервал пошуку звужується в околі точного розв'язку.
. Тобто інтервал пошуку звузився до x Î[0,708204, 1,85410]. Таким чином з кожною ітерацією інтервал пошуку звужується в околі точного розв'язку.


