
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи багатовимірного пошуку
У методі покоординатного спуску в області D задають початкове наближення Х 0 = Для цього розглядають функцію однієї змінної
Далі розглядають функцію однієї змінної
Після n кроків одержують
У результаті n кроків покоординатного спуску відбувається перехід із точки Х 0 у точку Х 1 = Якщо f (Х 0) = f (Х 1), то Х 0 є точкою мінімуму f (Х). Якщо f (Х 0) > f (Х 1), то виконують наступний крок покоординатного спуску, в якому за початкову точку взято Х 1. У результаті знаходять точку Х 2 і так далі. Цей процес продовжують доти, доки не виконають умову закінчення ітерацій, наприклад:
де e – задана відносна точність розв’язку. Координати нової точки знаходять за виразом
де h – крок пошуку; A i – випадковий напрямок. Точка X i +1 вважається обчисленою, якщо Наприклад. Знайти мінімум цільової функції
методом покоординатного спуску. Легко бачити, що цільова функція (9.2) досягає мінімуму в точці Оберемо початкове наближення
Знайдемо мінімум функції
Мінімум цієї функції є Проведемо ще одну ітерацію.
Тоді Як видно, точка X 2 ще більш наблизилась до c.
Градієнтні методи Відомо, що градієнт ортогональний до поверхні рівня цільової функції в точці його визначення і збігається з напрямом найшвидшого зростання цільової функції. Тому напрям, протилежний градієнту, вказує напрямок зменшення цільової функції, тобто напрямок, де може бути розташований мінімум функції.
Усі градієнтні методи використовують указані особливості поведінки градієнта, а стратегія їх пошуку будується на рекурентному виразі типу:
де h – величина кроку; а S i – одиничний вектор напряму пошуку на i- му кроці. Спосіб вибирання кроку, напряму чи того й другого одночасно визначає сутність методу. У разі пошуку мінімуму цільової функції потрібно рухатися в напрямі, протилежному градієнту функції точки f (X). Тому напрям
дозволяє одержати таку рекурентну формулу для методу градієнтного спуску:
Особливістю методу найшвидшого спуску є рух з оптимальним кроком, розрахованим за допомогою одновимірної мінімізації цільової функції по h уздовж антиградієнтного напряму. Дійсно, якщо в точці X i напрям пошуку визначений, то значення цільової функції в наступній точці X i +1 є функцією кроку спуску:
Тому крок h можна вибрати так, щоб
Вибір оптимального кроку зводиться до розв’язання одновимірної оптимізації функції g (h). Алгоритм методу найшвидшого градієнтного спуску: 1. Обчислити всі частинні похідні цільової функції. 2. Знайти один з методів одновимірного пошуку оптимального кроку уздовж антиградієнтного напряму. Крок h визначають з умови мінімуму функції 3. Обчислити координати нової точки 4. Якщо умова припинення пошуку не виконується, то перейти до кроку 1. Наприклад: Знайти мінімум цільової функції (9.2) методом найшвидшого градієнтного спуску. Знайдемо градієнт цільової функції
Оберемо початкове наближення Тоді
Знайдемо мінімум функції
Виконаємо ще одну ітерацію.
Таким чином
Контрольні завдання 1. Вибрати одновимірну цільову функцію відповідно до свого варіанта. 2. Знайти інтервали унімодальності цільової функції. 3. В межах інтервалу унімодальності знайти мінімум функції методом золотого перетину.
Варіанти завдань
4. Вибрати двовимірну цільову функцію відповідно до свого варіанта. 5. Знайти мінімум функції методом покоординатного спуску. 6. Знайти мінімум функції методом градієнтного спуску. 7. Порівняти результати. Варіанти завдань
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.146.223 (0.028 с.) |
 і послідовно проводять одновимірні пошуки вздовж різних напрямів, паралельних координатним осям.
і послідовно проводять одновимірні пошуки вздовж різних напрямів, паралельних координатним осям. і методом одновимірного пошуку знаходять
і методом одновимірного пошуку знаходять  Значення х 1, що відповідає мінімуму, позначають через
Значення х 1, що відповідає мінімуму, позначають через  :
:
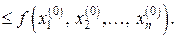
 і знаходять
і знаходять  Значення
Значення  , що відповідає мінімуму функції, позначають через
, що відповідає мінімуму функції, позначають через  . При цьому
. При цьому

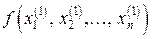
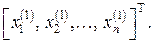
 ,
,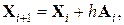
 . Інакше роблять спробу досягти успіху або за рахунок зміни кроку, або за рахунок зміни напряму на протилежний. Якщо всі спроби виявляються невдалими, то вибирають новий випадковий напрям пошуку. Випадковий напрям пошуку знаходять за допомогою випадкової точки A = [ a 1, a 2,…, an ], компоненти якої є випадковим значенням, рівномірно розподіленим на відрізку [–1, 1].
. Інакше роблять спробу досягти успіху або за рахунок зміни кроку, або за рахунок зміни напряму на протилежний. Якщо всі спроби виявляються невдалими, то вибирають новий випадковий напрям пошуку. Випадковий напрям пошуку знаходять за допомогою випадкової точки A = [ a 1, a 2,…, an ], компоненти якої є випадковим значенням, рівномірно розподіленим на відрізку [–1, 1]. (9.2)
(9.2) .
. та розглянемо функцію однієї змінної
та розглянемо функцію однієї змінної .
.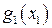 використовуючи один із методів одномірного пошуку, наприклад метод золотого перетину. Результатом є
використовуючи один із методів одномірного пошуку, наприклад метод золотого перетину. Результатом є 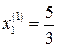 . Тепер розглянемо функцію
. Тепер розглянемо функцію .
.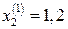 . В результаті першої ітерації отримуємо наступне наближення:
. В результаті першої ітерації отримуємо наступне наближення:  . Легко впевнитись, що
. Легко впевнитись, що  , а також в тому, що точка X 1 ближче розташована до c ніж X 0.
, а також в тому, що точка X 1 ближче розташована до c ніж X 0. .
. .
.
 .
.
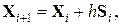

 . (9.3)
. (9.3)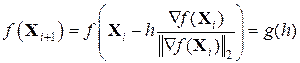 .
. максимально зменшила своє значення:
максимально зменшила своє значення: .
.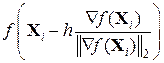 по h.
по h. за формулою (9.3).
за формулою (9.3). . (9.4)
. (9.4)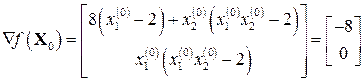
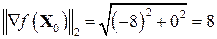


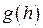 використовуючи один із методів одномірного пошуку, наприклад метод золотого перетину. Результатом є
використовуючи один із методів одномірного пошуку, наприклад метод золотого перетину. Результатом є  . Тоді
. Тоді .
. ;
; ;
;
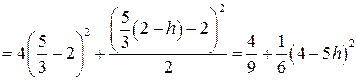 ;
;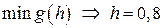 .
. .
.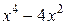 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
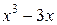 .
.
 .
.
 .
.
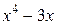 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
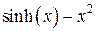 .
.
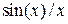 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
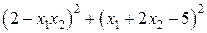 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
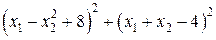 .
.
 .
.
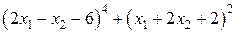 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



