
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о наилучшем использовании ресурсов
Постановка задачи. Фермер выращивает две культуры Х и Y на площади 160 га. Ему необходимо распределить землю, людей и технику таким образом, чтобы прибыль от реализации урожая названных культур была максимальной. В процессе выращивания каждой из культур необходимо выполнять три операции - вспашку, сев и уборку. В таблице 8.2 эти операции и время, необходимое для их выполнения, даны в привязке к четырем разным периодам производства; там же указано время в пределах каждого из периодов, которое может быть использовано в этих целях.
Таблица 8.3- К задаче распределения ресурсов при выращивании двух культур.
Пусть x3 и x4 обозначают площади, выделенные под культуру X, которые убирают в периоды 3 и 4 соответственно, и пусть y есть площадь, выделенная под культуру Y. Площади, выделяемые под каждую из культур, ограничены общей площадью угодий, то есть
Для уборки каждой культуры может быть использован самоходный комбайн одного и того же типа. Пусть bk есть число комбайнов, необходимое для уборки. Это число может быть только целым и неотрицательным. Сформулируем ограничения по общим затратам техники на уборку: период 3: период 4: Пусть для вспашки, сева и уборки необходим трактор. Пусть bt есть неотрицательная целочисленная переменная, обозначающая потребность в тракторах. Тогда период 1: период 2: период 3: период 4: Потребности в трудовых ресурсах рассчитывается следующим образом. Во время вспашки и сева требуется один человек для управления трактором. Чтобы убрать культуру X, требуется два человека для управления комбайном и один - для управления трактором. Во время уборки культуры Y требуется по одному человеку для управления комбайном и трактором. Пусть bl есть целочисленная переменная, обозначающая полную потребность в людях. Тогда ограничения по труду (в чел.* ч) можно сформулировать следующим образом: период 1: период 2: период 3: период 4: Культуру Y можно выращивать на одном и том же поле только один год из двух, а культуру X — два года из трех. Фермер намерен выращивать их ежегодно и поэтому должен предусмотреть в своих планах севооборот. Это можно сделать с помощью ограничений:
Доход, получаемый от культур X и Y, равен 2 и 4 ед/га. Соответствующие ежегодные затраты труда, комбайнов и тракторов равны 15 ед/чел., 3 ед/маш. и 1,5 ед/маш. Целевая функция (функция полезности, доход) F, ед/год, которую необходимо максимизировать, имеет вид
Таким образом, задача формализуется по схеме частично-целочисленного линейного программирования, имеет шесть управляемых переменных (x3, x4,y, bl, bk., bt) и ограничений (уравнения 8.31 ….8.35): максимизировать
с учетом ограничений:
bl ≥ 0, bk. ≥ 0, bt ≥ 0 - целые числа. Оптимальное решение данной задачи при приведенных исходных данных и условиях будет следующим: F = 204, x3 = 80, x4 =0, y = 80, bl = 16, bk. = 8, bt = 8.
Транспортная задача
Постановка задачи. Пусть имеется m поставщиков некоторой однородной продукции. Считается, что i - ый поставщик располагает ai единицами продукции, i = 1, 2, …, m. Продукцию поставщиков используют n потребителей, потребности которых равны b1, b2 , …, bn единиц продукции. Все числа ai и bj положительны. Кроме того, известна стоимость перевозки единицы продукции от i -го поставщика j -ому потребителю: cij, i = 1, 2, …, m; j = 1, 2, …, n. Продукция однородна, поэтому любой поставщик может предложить ее любому потребителю, рис.8.10. Требуется определить такое количество единиц продукции, перевозимой от каждого поставщика к каждому потребителю, чтобы транспортные расходы были минимальны и потребности всех потребителей были удовлетворены. Задача предполагается разрешимой в том смысле, что общий объем поставок должен быть не меньше общего объема потребностей. Обозначим через xij число единиц продукции, перевозимой от i- го поставщика j -ому потребителю. Тогда транспортные расходы этой пары поставщик- потребитель составят cij*xij, а общая стоимость всех перевозок (от каждого поставщика каждому потребителю) равна:
Тот факт, что потребности каждого потребителя должны быть полностью удовлетворены запишем в виде неравенства:
Условие осуществимости поставок, наличия продукции у поставщика выполняется неравенством:
j
Рис.8.10- Поставщики и потребители продукции.
Кроме того, все величины должны быть неотрицательны. Таким образом, транспортная задача принимает вид следующей задачи линейного программирования:
xij ≥ 0, i = 1, 2, … n; j = 1, 2, …m. В этой задаче m*n переменных и m+n ограничений (не считая условий неотрицательности пременных). Если суммарные возможности поставок совпадают с требуемой суммарной потребностью
то можно так организовать перевозки, чтобы вся имеющаяся у поставщиков продукция была вывезена и каждый потребитель получил необходимое количество продукции. В этом случае транспортная задача принимает вид канонической задачи линейного программирования и называется закрытой транспортной задачей:
Если
то спрос потребителей будет удовлетворен, но у поставщиков останется лишняя продукция. Случай
соответствует ситуации, когда потребности потребителей не могут быть удовлетворены полностью. Этот случай с самого начала был исключен в постановке задачи. Закрытая транспортная задача всегда имеет оптимальное решение. Это решение можно найти с помощью симплекс-метода. Однако обычно для решения транспортной задачи используют специальные методы, учитывающие специфику каждой задачи. Приведем пример постановки и решения транспортной задачи. Постановка задачи. В районе имеются два склада зерна (два хозяйства по производству зерна) и два элеватора. Ежедневно с первого склада вывозят 50 т зерна, а со второго - 70 т на элеваторы, причем на первый - 40 т, а на второй - 80 т. Обозначим через сij стоимость перевозки 1 т зерна с i- го склада на j -й элеватор (i, j = 1,2). Пусть с11 = 1,2, с12 = 1,6, с21 = 0,8, с22 = 1.0. Как нужно спланировать перевозки, чтобы их стоимость была минимальной? Придадим задаче математическую формулировку. Обозначим через x1 и x2 количество зерна, которое надо перевезти с первого склада на первый и второй элеваторы, а через x3 и x4 - со второго склада на первый и второй элеваторы соответственно. Тогда: x1 + x2 = 50, x3 + x4 = 70, x1 + x3 = 40, x2 + x4 = 80. (8.45) Общая стоимость всех перевозок определяется формулой: F = 1,2x1 + 1,6x2 + 0,8x3 + x4. С математической точки зрения, задача заключается в том, чтобы найти четыре числа x1, x2, x3 и x4, удовлетворяющие всем заданным условиям и дающие минимум функции F. Решим систему уравнений (8.45) относительно xi (i = 1, 2, 3, 4) методом исключения неизвестных. Получим, что x1 = x4 – 30, x2 = 80 – x4, x3 = 70 – x4, а x4 не может быть определено однозначно. Так как xi > 0 (i = 1, 2, 3, 4), то из вышеприведенных уравнений следует, что 30 < x4 < 70. Подставляя выражение для x1, x2, x3 в формулу для F, получим: F = 148 – 0.2x4 . Минимум этой функции достигается при максимально возможном значении x4 = 70. Соответствующие значения других неизвестных составят: x1 = 40, x2 = 10, x3 = 0. Контрольные вопросы к главе 8 1. Дайте определение временного ряда. 2. Назовите этапы этапы анализа временного ряда при прогнозировании. 3. Для чего при анализе временного ряда используют его тренд? 4. Какие виды уравнений используют для аналитической модели полета зерна? 5. Как решаются системы неоднородных дифференциальных уравнений? 6. Дайте определение методу моделирования, использующего линейное программирование. 7. Перечислите типы задач, решаемые с помощью линейного программирования. 8. Дакйте определение целевой функции в задаче линейного программирования. 9. В чем назначения ограничений и условий при решении задач линейного программировыания?
10. Назовите оператор в Matlab, с помощью которого можно существляют решение задачи линейного программирования. 11. Каким образом задачу на максимум целевой функции превратить на ее минимум.
Источники информации к главе 8 1. Каюмов М.К. Программирование урожаев сельскохозяйственных культур. – М.: Агропромиздат, 1988.- 320 с.:ил. 2. Мухин О.И. 3. Иозайтис В.С., Львов Ю.С. Экономико-математическое моделирование производственных систем: Учебное пособие для инженерно-экономических спец. вузов.- М.: Высш. шк., 1988.- 192 с.: ил. 4. Орлов А.И. Прикладная статистика М.: Издательство «Экзамен», 2004. 5. Рыжиков Ю.И. Имитационное моделирование. Теория и технология.- СПб.: КОРОНА принт; М.: Альтекс- А, 2004.- 384 с., ил. 6. Тихонов А.И., Кальнер Н.К., Класко П.М. Математическое моделирование технологических процессов. Минск: Наука и техника, 1980, - 256 с. 7. Трахтенгерц Э.Л. Компьютерная поддержка принятия решений. М., Синтэг, 1988. 8. Франс Дж., Торнли Дж.Х.М. Математические модели в сельском хозяйстве/ Пер. с англ. А.С.Каменского; под ред.Ф.И.Ерешко. Предисл.Ф.И.Ерешко и А.С. Каменского.- М.: Агропромиздат, 1987.400 с.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.241.82 (0.023 с.) |

 . (8.31)
. (8.31) ; (8.32)
; (8.32)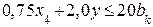 .
.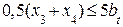 ≤ 5 * bt; (8.33)
≤ 5 * bt; (8.33) ;
; t;
t; .
. ≤ 5 * bt; (8.34)
≤ 5 * bt; (8.34) ;
; t;
t; .
.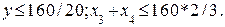 (8.35)
(8.35) . (8.36)
. (8.36)
 . (8.38)
. (8.38) (8.39)
(8.39) (8.40)
(8.40)
 (8.41)
(8.41) (8.42)
(8.42)
 (8.43)
(8.43)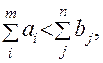 (8.44)
(8.44)


