Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системный анализ и управление грузопотоками по экономическому критерию путем решения транспортной задачи линейного программированияСодержание книги
Поиск на нашем сайте
Транспортная задача линейного программирования формулируется следующим образом. Имеется m пунктов отправления А1, А2,.... Аm в которых находятся запасы какого-то однородного груза в количестве соответственно а1, а2,..... аm единиц. Кроме того, имеется n пунктов назначения В1, В2,...... Вn, подавших заявки соответственно на b1, b2,.... bn единиц груза. Предполагается, что сумма всех заявок равна сумме всех запасов, т.е.
Известна стоимость сi j перевозка единицы товара от каждого пункта отправления Аi до каждого пункта назначения В j. Матрица стоимостей С имеет вид:
Требуется составить такой план перевозок, при котором все заявки были бы выполнены и общая стоимость всех перевозок была минимальна. Таким образом, в качестве критерия выбрана стоимость перевозки груза. Критериями в транспортной задаче могут быть следующие показатели: расстояние, время, мощность и др. Транспортная задача, в которой выполняется условие (8.1), называется закрытой. Задача, в которой это условие не выполняется, называется открытой. В данной теме рассматривается закрытая транспортная задача. Математическая формулировка транспортной задачи может быть представлена в следующем виде: пусть xi j ¾ количество груза, отправляемого из i-го пункта отправления Аi в j-й пункт назначения Вj( Переменные xij должны удовлетворять неравенствам
Любую совокупность значений xij ( Оптимальный план ¾ это такой план, который среди всех допустимых имеет наименьшую стоимость перевозок. Отыскание оптимального плана выполняется с помощью транспортной табл.8.1.
Таблица 8.1.
Стоимость перевозок сij помещают в правом верхнем углу клеток таблицы. Клетки таблицы, в которых будем записывать отличные от нуля перевозки xij, называются базисными. Таких клеток не более чем m+n-1. Пустые клетки называются свободными, их не менее (m-1)(n-1). Все дальнейшие действия по нахождению решения транспортной задачи будут сводится к преобразованию транспортной табл.8.1, т.е. к двум этапам:
а) отыскание первого решения методом «северо-западного угла»; б) нахождение оптимального решения потенциалов. Продемонстрируем применение этого метода на примере транспортной табл.8.2. Таблица 8.2
Начнем заполнения транспортной таблицы с левого верхнего («северо-западного») угла. Пункт В1 подал заявку на 18 единиц груза. Удовлетворим её из запасов А 1. После этого в нем ещё останется 30 -18 = 12 единиц груза. Отдадим их пункту В2. Но заявка этого пункта еще не удовлетворена. Выделим недостающие 15 единиц из запасов пункта А 12 и т.д. применяя такую методику, заполним до конца перевозками x ij транспортную табл.8.3. Таблица 8.3
В полученном опорном решении базисных клеток r = n + m -1 = 5 + 4 - 1 = 8, свободных клеток (m - 1)(n - 1) = 3 × 4 = 12. Опорный план, получаемый в результате применения метода «северо-западного угла», как правило, не оптимальный. Поэтому для отыскания оптимального решения применяется метод потенциалов.
После того как с помощью метода «северо-западного угла» найден первый опорный план, выполним его улучшение с помощью метода потенциалов. Алгоритм метода показан на рис.8.1. Улучшение плана перевозок в этом методе выполняется с помощью перемещения перевозок из клетки в клетку в транспортной таблице без нарушения баланса заявок и запасов. Перемещение грузов в таблице выполняется по замкнутому циклу.
Рисунок 8.1.Схема алгоритма метода потенциалов.
Циклом в транспортной таблице называются несколько клеток, соединенных замкнутой ломаной линией, которая совершает поворот на 90° в отдельных клетках. Цикл стоят так, чтобы одна его вершина была в свободной клетке, остальные вершины в базисных (заполненных) клетках. Существует теорема, согласно которой для любой свободной клетки транспортной таблицы всегда существует цикл (притом единственный), одна из вершин которого лежит в этой сводной клетке, а все остальные ¾ в базисных клетках. В каждой цикле заменяют одну свободную переменную на базисную, т.е. заполняют одну свободную клетку и в замен освобождают одну из базисных клеток. Цикл имеет четное число вершин. Будем отмечать знаком «+» те термины, в которых в результате перемещения грузов перевозки увеличиваются, а знаком «-», вершины в которых они уменьшаются. Перенести (перебросить) какое-то количество единиц груза по циклу ¾ это значит увеличить перевозки, стоящие в положительных вершинах цикла, на это количество единиц, а перевозки, стоящие в отрицательных вершинах, уменьшить на то же количество. При переносе любое количество единиц по циклу равновесие между запасами и заявками не меняется. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число груза, возникают отрицательные перевозки). Изменение стоимости перевозок при перемещении одной единиц груза по циклу называют ценой цикла. Определяется цена цикла как алгебраическая сумма стоимостей, стоящих в вершинах цикла, причем, стоимости, стоящие в положительных вершинах, берутся со знаком «+», а в отрицательных ¾ со знаком «-». Для улучшения плана перевозок целесообразно перемещать перевозки только по тем циклам, цена которых отрицательна. Метод потенциалов позволяет автоматически выделять циклы с отрицательной ценой и определить их цены. Для этого поставим в соответствие каждому пункту отправления (столбцу) Аi число a i, а каждому пункту назначения (строке) Вj ¾ число b j. Эти числа называются потенциалами. Определим значения a i и b j. Для этого составим для базисных клеток m + n - 1 уравнений c m + n неизвестными, т.е.
Система (8.10) имеет бесконечное число решений. Поэтому для нахождения одного из них примем a 1 = 0. Решая m + n - 1 уравнений (8.10) методом подстановок, находим остальные потенциалы
Затем для незаполненных клеток вычисляют псевдостоимоти по формуле
Для каждой незаполненной клетки цена цикла пересчета равна разности между стоимостью с ij и псевдостоимостью с¢ ij. Следующим шагом алгоритма является проверка опорного решения на оптимальность (рис.8.1).
Если для базисных клеток плана (x ij >0)
то план является оптимальным и никаким способом улучшен быть не может. Это означает, что циклы с отрицательной стоимостью отсутствуют. Если хотя бы в одной свободной клетке псевдостоимость больше стоимости Обычно для построения цикла выбирают свободную клетку с наименьшей отрицательной ценой При решении транспортной задачи может быть получено вырожденное решение, когда количество базисных переменных меньше. В этом случае одна или несколько базисных клеток останутся незаполненными, что затрудняет расчет потенциалов в решение задачи. Поэтому для ликвидации вырождения ставят ноль в незаполненную базисную клетку (или клетки). Базисная клетка с нулевой перевозкой тем будет отличаться от свободной, что в ней нуль проставлен, а в свободной нет. Дальнейшие манипуляции с транспортной задачей будут совершенно такими же, если бы в базисных клетках стояли только положительный перевозки, с той лишь разницей, что, когда одна из отрицательных вершин цикла окажется в базисной клетке с нулевой перевозкой, нужно переносить по этому циклу нулевую перевозку. Решим задачу, сформулированную в табл.8.2. В результате применения метода «северо-западного угла» полученное первое опорное решение, которое занесено в табл.9.4 для дальнейших расчетов. Таблица 8.4.
b 1 =13; b 2 = 7; b 3 = 11; b 4 = 9; b 5 = 14.
Значений целевой функции будет Определим потенциалы из уравнений:
Приняв a 1 = 0. Найдем a 2 = 1, a 3 = -1, a 4 = 1, b 1 =13; b 2 = 7; b 3 = 11; b 4 = 9; b 5 = 14. Подсчитаем для незаполненных клеток псевдостоимости по формуле
Результаты запишем в табл.8.4. Псевдостоимости будем заносить в левый верхний угол незаполненных клеток. Анализируя табл.8.4 приходим к выводу, что опорное решение не оптимально и может быть улучшено. Наименьшая отрицательная цена
Поэтому построим на клетке (1, 5) цикл (табл.8.4). Выполним перемещение грузов по циклу, результаты поместим в табл.8.5. Дальнейшие расчеты выполнены в табл.8.6. ¾ 8.10. Таблица 8.5
b 1 =13; b 2 = 7; b 3 = 11; b 4 = 9; b 5 = 14. Z = 1343 Таблица 8.6.
b 1 =13; b 2 = -4; b 3 = 0; b 4 = 0; b 5 = 5. Z = 1332
Таблица 8.7.
b 1 =13; b 2 =13; b 3 =17; b 4 = 17; b 5 = 5.
Z = 1094
Таблица 8.8.
b 1 =3; b 2 =3; b 3 =7; b 4 = 7; b 5 = 5. Z = 1054. Таблица 8.9.
b 1 =9; b 2 =9; b 3 =13; b 4 = 7; b 5 = 5. Z = 988. Таблица 8.10.
b 1 =7; b 2 =7; b 3 =11; b 4 = 5; b 5 = 5. Z = 980.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.123.56 (0.012 с.) |

 . (8.1)
. (8.1) (8.2)
(8.2) ), xi j ³0.
), xi j ³0.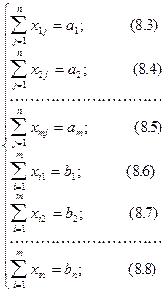
 . (8.9)
. (8.9)



 (8.10)
(8.10)
 .
. ,
, , то план не является оптимальным и может быть улучшен переносом грузов по циклу, соответствующему данной свободной клетке.
, то план не является оптимальным и может быть улучшен переносом грузов по циклу, соответствующему данной свободной клетке. . Далее на этой клетке строят цикл, выполняют переброску грузов по циклу, в результате чего определяют новый опорный план. Если полученный опорный план все еще не оптимален, процедура улучшения продолжается до тех пор, пока не будет найден оптимальный план (8.1).
. Далее на этой клетке строят цикл, выполняют переброску грузов по циклу, в результате чего определяют новый опорный план. Если полученный опорный план все еще не оптимален, процедура улучшения продолжается до тех пор, пока не будет найден оптимальный план (8.1). .
.