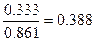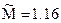Расчёт локальных приоритетов. Синтез приоритетов.

Рассмотрев методику расчёта вектора приоритетов для матрицы парных сравнений и методику оценки степени согласованности суждений анализируемой матрицы, перейдём теперь к рассмотрению основного вопроса – анализа проблемы методом анализа иерархий.

Для того чтобы решить проблему, сформулированную в примере, описанном в начале главы, то есть, чтобы выбрать дом и решить жилищную проблему, необходимо выполнить следующее.

После построения иерархической модели проблемы (рис. 7.3,б) начинаем первый этап анализа, который состоит в исследовании степени влияния показателей свойств качества дома на общее удовлетворение домом. В формальном виде этот этап состоит в анализе влияния факторов второго уровня иерархии на цель анализа – первый уровень. В табл. 7.4 представлена матрица парных сравнений для восьми факторов 2-го уровня, заполненная суждениями эксперта, квалиметрированными по шкале Саати.

Напомним, что суждение высказывается по поводу степени предпочтения фактора, указанного левой колонке матрицы, по отношению к фактору, указанному в соответствующем столбце матрицы. Например, эксперт отвечает на вопрос: “насколько фактор “ размеры дома ” предпочтительнее фактора “ время постройки дома ” по отношению к цели “ общее удовлетворение домом ”.

В данной матрице эксперт высказал суждение, что первый фактор имеет значительное превосходство по важности по сравнению со вторым фактором и по шкале Саати оценил это превосходство числом 7. Соответственно обратное превосходство (второго фактора над первым) оцененно по шкале Саати как 1/7.

В правой колонке табл. 7.4. представлены компоненты вектора приоритетов, а внизу таблицы:

λ _max – наибольшее собственное значение матрицы суждений;

ИС – индекс согласованности;

ОС – отношение согласованности.

Таблица 7.4.

Общее удовлетворение домом	Размер дома	Удобство автобусной остановки	Окрестности	Время постройки дома	Двор	Современное оборудование	Общее состояние	Финансовые условия	Вектор приоритетов
Размеры дома							1/3	¼	0.173
Удобство автобусной остановки	1/5		1/3				1/5	1/7	0.054
Окрестности	1/3							1/5	0.188
Время постройки дома	1/7	1/5	1/6		1/3	1/4	1/7	1/8	0.018
Двор	1/6	1/3	1/3			1/2	1/5	1/6	0.031
Современное оборудование	1/6	1/3	1/4				1/5	1/6	0.036
Общее состояние			1/6					1/2	0.167
Финансовые условия									0.333

 

λmax=9.67 ИС=0.238 ОС=0.17

 

Следует отметить, что отношение согласованности для данной матрицы несколько больше рекомендованного уровня (ОС ≤ 0.1), однако для задач используемого типа его можно принять.

В общем случае уровень согласованности должен соответствовать тому риску, который сопутствует работе с несогласованными данными.

Например, при сравнении воздействия лекарств на организм необходимо иметь очень высокий уровень согласованности.

Прокомментируем кратко полученные после обработки матрицы результаты. Наиболее значительным с семейной точки зрения оказался фактор “ финансовые условия ” (Р=0.333), “вес” которого почти в два раза больше ближайшего к нему и достаточно значимого фактора “ окрестности ” (Р=0.188). наименьший интерес вызвал такой фактор как “ время постройки дома ” (Р=0.018).

Четыре такие фактора как “размеры дома” (0.173), “окрестности“ (0.188), ”общее состояние” (0.167), “финансовые условия” (0.333) доминируют над остальными, занимая почти 90% от общего “веса” воздействия факторов. Для упрощения задачи эти факторы могут быть оставлены для дальнейшего рассмотрения, так как они окажут наибольшее влияние на окончательный выбор дома.

Если такое решение принимается, то оставляемые факторы перенормируются. Для этого следует разделить каждое значение оставленной компоненты на сумму оставленных компонент.

В нашем примере перенормировка представлена в табл. 7.5.

Таблица 7.5.

	Факторы
	Размеры дома	Окретности	Общее сос- Тояние	Финансовые условия	∑
“веса” факторов из таблицы 7.4.	0.173	0.188	0.167	0.333	0.861
Перенормированные “веса” факторов

Однако в нашем примере будут рассматриваться все восемь факторов для проведения процесса анализа в полном объёме.

Переходим теперь к рассмотрению влияния факторов третьего уровня на факторы второго уровня, то есть к анализу «веса» (предпочтительности) каждого из рассматриваемых домов (А, Б, В) по отношению к каждому фактору второго уровня. Для этого необходимо сформировать и обработать восемь экспертных матриц парного сравнения. Сами матрицы и результаты их обработки в виде главных векторов и мер согласованности представлены в табл. 7.6.

Таблица 7.6.

Размеры дома	А	Б	В	Вектор приоритетов	Двор	А	Б	В	Вектор приоритетов
А				0.754	А				0.674
Б	1/6			0.181	Б	1/5		1/3	0.101
В	1/8	1/4		0.065	В	1/4			0.226
				λmax=3.136 ИС=0.068 ОС=0.117					λmax=3.086ИС=0.043 ОС=0.074
Окрестности	А	Б	В	Вектор приоритетов	Современное оборудование	А	Б	В	Вектор приоритетов
А				0.745	А				0.747
Б	1/8		¼	0.065	Б	1/8		1/5	0.060
В	1/6			0.181	В	1/6			0.193
				λmax=3.13 ИС=0.068 ОС=0.117					λmax=3.197 ИС=0.099 ОС=0.170
Удобство автобусных маршрутов	А	Б	В	Вектор приоритетов	Общее состояние	А	Б	В	Вектор приоритетов
А			1/5	0.233	А		½	½	0.200
Б	1/7		1/8	0.005	Б				0.400
В				0.713	В				0.400
				λmax=3.25 ИС=0.124 ОС=0.213					λmax=3.000 ИС=0.000 ОС=0.000
Время постройки дома	А	Б	В	Вектор приоритетов	Финансовые условия	А	Б	В	Вектор приоритетов
А				0.333	А		1/7	1/5	0.072
Б				0.333	Б				0.650
В				0.333	В		1/3		0.278
				λmax=3.000 ИС=0.000 ОС=0.000					λmax=3.065 ИС=0.032 ОС=0.056

Анализ векторов локальных приоритетов показывает. Что дом А лучший по четырём критериям (размер дома, окрестности, двор и современное оборудование), дом Б лучший по финансовым условиям, а дом В лучший по удобствам расположения автобусных стоянок.

На следующем этапе осуществляется синтез локальных приоритетов или оценка обобщенных (глобальных) приоритетов. В нашем примере, идёт речь о получении вектора глобальных приоритетов домов (А, Б, В) по отношению к цели верхнего уровня – общего удовлетворения домом.

Для этого матрицу векторов локальных приоритетов 2-го уровня, составленную по результатам анализа, представленного в таблице 7.6, умножают на вектор локальных приоритетов 1-го уровня, полученных в таблице 7.4, т.е.:

Например, первая компонента обобщенного вектора приоритетов получается так:

(0.754 х 0.173)+(0.754 х 0.188)+(0.233 х 0.054)+…+(0.072 х 0.333)=0.396

В результате получаем обобщенный (глобальный) вектор приоритетов домов (А, Б, В) по отношению к конечной цели – покупке дома, от которого семья получает удовлетворение. Этот вектор имеет вид:

Дом	Вектор приоритетов
А	0.396
Б	0.341
В	0.263

Таким образом, с учётом всех рассматриваемых факторов, предпочтение при покупке отдается дому А.

На заключительном этапе осуществляется оценка степени согласованности всей рассматриваемой иерархии, рассчитываемой по мерам согласованности всех уровней иерархии.

Расчёт обобщенной меры согласованности продемонстрируем на рассматриваемом примере.

Вначале оцениваем индекс согласованности, продемонстрируем иерархии М как сумму индекса согласованности иерархии первого уровня и индекса согласованности второго уровня, представляющего собой взвешенную сумму индексов согласованностей матриц второго уровня (см. табл. 7.4 и 7.5).

Рассчитываем вначале индекс согласованности 2-го уровня как произведение вектора-строки индексов согласованности 2-го уровня на вектор приоритетов 1-го уровня (вектор-столбец). Получаем:

Вектор-строка Вектор-столбец

 

Обобщённый индекс согласованности:

М = 0.238 + 0.0468 = 0.285

Затем аналогичным способом вычисляется суммарный случайный индекс

Величина отношения согласованности для всей иерархичной структуры