
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы имитации случайных факторов при имитационном моделировании.Содержание книги
Поиск на нашем сайте
Имитационный системный анализ поведения сложных объектов и процессов выполняется с учётом воздействий внешней среды. Возмущающие воздействия внешней среды являются, как правило, случайными процессами с характерными законами распределения и автокорреляционными функциями. При имитационном моделировании случайных факторов и возмущающих воздействий необходимо получить случайную последовательность чисел, имеющих такой же закон распределения и такую же автокорреляционную функцию, что и закон распределения и автокорреляционная функция реальных возмущающих воздействий. Базовой последовательностью случайных чисел для решения этой задачи является совокупность случайных чисел с равномерным законом распределения:
Псевдослучайные числа a можно получать программно, например с использованием формулы:
где Последовательность чисел с нормальным законом распределения может быть получена в соответствии с выражением:
где Пусть автокорреляционная функция
Рис. 6. 2. График автокорреляционной функции возмущающего воздействия. Коррелированные случайные числа
где Параметры формирующего фильтра находятся путём решения системы
где Система уравнений (6. 5) решается методом Ньютона. Приближение корней системы уравнений (6. 5) выполняется в соответствии с реккурентным соотношением Ньютона:
где Поиск вектора корней первого приближения выполняется в такой последовательности: 1. Задаются нулевым приближением корней
2. Вычисляют значения вектор функции корней нулевого приближения:
3. Вычисляют матрицу производных от вектор функции
С учётом (6. 9), получаем:
В матрицу (6. 11) подставляют значения корней нулевого приближения 4. Обратную матрицу производных от вектор функции 5. Подставляют значения в формулу (6. 6) и находят вектор корней нулевого приближения. Аналогично находят векторы корней первого, второго и последующих приближений параметров формирующего фильтра. Приближение корней выполняют до тех пор, пока:
где Имитация случайных чисел с любым, кроме нормального, законом распределения может быть выполнена методом обратных функций. Он основан на использовании следующей теоремы. Если х случайная величина, равномерно распределённая на отрезке [0;1], то случайная величина y является решением уравнения
Имеет плотность распределения Таким образом последовательность чисел x0, x1, x2,…, xi преобразуется в последовательность чисел y0, y1, y2,…, yi имеющую заданную плотность распределения Пример: Необходимо получить последовательность чисел, имеющих распределения по показательной функции:
В соответствии с (6.13) имеем:
откуда
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.17 (0.006 с.) |

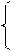
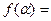

 ,
, 


 (6.1)
(6.1) (6.2)
(6.2)
 (6.3)
(6.3)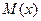 - математическое ожидание случайных чисел x;
- математическое ожидание случайных чисел x;  среднеквадратическое отклонение случайных чисел x;
среднеквадратическое отклонение случайных чисел x;  - равномерно распределённые случайные числа;
- равномерно распределённые случайные числа; 
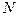 - количество некоррелированных, случайных чисел с нормальным законом распределения.
- количество некоррелированных, случайных чисел с нормальным законом распределения. возмущающего воздействия
возмущающего воздействия 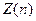 имеет вид:
имеет вид:

 получают в соответствии с выражением:
получают в соответствии с выражением: (6.4)
(6.4)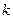 -номер коррелированного случайного числа;
-номер коррелированного случайного числа; 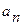 - параметры формирующего фильтра;
- параметры формирующего фильтра; 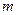 - количество коэффициентов.
- количество коэффициентов. 
 , (6.5)
, (6.5) -значения автокорреляционной функции, которые берутся из графика (рис. 6. 2.).
-значения автокорреляционной функции, которые берутся из графика (рис. 6. 2.).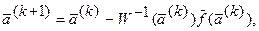 (6.6)
(6.6) - векторы к-го (к+1) приближения корней системы;
- векторы к-го (к+1) приближения корней системы;  - вектор, функция к-го приближения корней;
- вектор, функция к-го приближения корней;  - обратная матрица производных от вектор функции
- обратная матрица производных от вектор функции 
 то есть при К=0.
то есть при К=0. (6. 7)
(6. 7) (6. 8)
(6. 8)
 (6. 9)
(6. 9)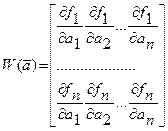 (6. 10)
(6. 10)
 (6. 11)
(6. 11)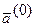 и получим матрицу
и получим матрицу 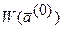 .
. получают методом Гаусса.
получают методом Гаусса. (6. 12)
(6. 12) - заданная точность вычислений.
- заданная точность вычислений. , (6. 13)
, (6. 13) где
где  - заданный закон распределения реакции возмущающего воздействия.
- заданный закон распределения реакции возмущающего воздействия. .
.



 ,
, .
.


