Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение графа, виды графов.Содержание книги
Поиск на нашем сайте
Пусть определено некоторое множество элементов V. Граф G=G(V) считается определённым, если задано некоторое множество сочетаний элементов или пар вида E=(a, b), где a, b ÎV, указывающие, какие элементы считаются связанными. Пара E=(a, b) называется ребром, a, b – вершинами. Если порядок расположения концов безразличен, т.е. если E=(a, b)=(b, a), то говорят, что E – неориентированное ребро, если порядок важен, то говорят, что E – ориентированное ребро. Ребро Е инцидентно (т.е связано) с вершинами a, b, и вершины a, b инцидентны ребру Е. Граф, составленный из неориентированных рёбер, называется неориентированным, а составленный из ориентированных рёбер называется ориентированным графом. Есть смешанные графы. Неориентированный граф G может быть превращён в ориентированный при помощи процесса удвоения, состоящего в замене каждого ребра парой рёбер с теми же концами и приписывании им противоположных ориентаций.
3.2.2 Способы задания графов. А. Графическое представление. Достоинство – наглядность. Недостаток – не может быть использовано при решении задач структурного анализа с помощью ЭВМ. Б. Матричное представление. 1) Матрица смежности для вершин неориентированного графа: А= a i,j = {1 при наличие связи; 0 при отсутствии связи Матрица смежности для вершин ориентированного графа. a i,j = {1, если из вершины i можно перейти в вершину j; 0 в противном случае 2) Матрица инциндентности В= z – для неориентированного графа:
b i,j = {1, если i-я вершина инцидентна данному j-му ребру (есть связь); 0, если нет связи; для ориентированного графа: b i,j = {1, если i-я вершина есть начало j-го ребра; -1, если i-я вершина есть конец j-го ребра; 0, если i-я вершина не инцидентна j-му ребру. В. Множественное представление. В этом случае для ориентированного графа G(V) задаётся множество вершин V и соответствие G, которое показывает, как связаны между собой вершины. Для каждой вершины i соответствие G определяет множество вершин G(i), в которые можно непосредственно попасть из вершины i. В ряде случаев G(i) называется множеством правых инциденций. Множество Пример: Способы формализации исходной структуры системы.
Рис. 3.1 Структура системы. Рис. 3.2 Граф системы.
Матрица смежности вершин А:
Матрица инцинденций вершин В:
i=1,2,3,4,5 кол-во вершин, j=1,2,3… 7 кол-во рёбер. Множественное задание структуры системы сводится к системе множеств: G(1)=(2,3) G(2)=0 G(3)=(4,5) G(4)=(2) G(5)=(1,2)
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |


 , где n – число вершин в графе.
, где n – число вершин в графе.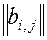 i=1, 2… n j=1, 2… m, где n – число вершин, m – число рёбер;
i=1, 2… n j=1, 2… m, где n – число вершин, m – число рёбер;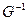 (i) определяет все вершины, из которых можно попасть в вершину i, а поэтому называется обратным соответствием.
(i) определяет все вершины, из которых можно попасть в вершину i, а поэтому называется обратным соответствием.