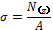Растяжение, сжатие брусьев, стержней»

ИСХОДНЫЕ ПОНЯТИЯ.

Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила N(z). Брусья с прямолинейной осью (прямые брусья), работающие на растяжение или сжатие, часто называют стержнями.

Рассмотрим невесомый, защемленный левым кондом прямой брус, вдоль оси, которого действует активная сила F и 2F (рис. 1.1.).

Части бруса постоянного сечения, заключенные между поперечными плоскостями, в которых приложены активные или реактивные силы, будем называть участками. Изображенный на рис. 2.1. брус состоит из двух участков.

Применив метод сечений, определим продольные силы N₁(z) и N ₂ (z) на участках. Рассечем брус на левом участке поперечным сечением 1—1. Во всех точках бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса (например, правой от сечения):

Z= 0; 2F- F- N,(z) = О,

откуда

N,(z) = 2F- F= F.

Мы видим, что для равновесия оставленной части бруса в сечении 1 — 1 необходимо приложить только силу N_h направленную вдоль оси, т.е. продольную силу.

Продольная сила есть равнодействующая нормальных внутренних сил, возникающих в поперечном сечении бруса. Нетрудно понять, что в сечении 2—2 на правом участке продольная сила будет иметь другое значение: N₂(z)~2F. Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса).

В дальнейшем растягивающие (направленные от сечения) продольные силы мы будем считать положительными, а сжимающие (направленные к сечению) — отрицательными.

При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле:

где N_(z)— продольная сила; A— площадь поперечногосечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет.

В сечениях, близких к точкам приложения растягивающих или сжимающих сил, закон распределения напряжений по сечению будет более сложным, но, пользуясь принципом смягченных граничных условий, мы будем этими отклонениями пренебрегать и

Рис. 2.1 считать, что во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно.

Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635—1703).

Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математический закон Гука можно записать в виде равенства:

 

Коэффициент пропорциональности Е - характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.

Модуль упругости и напряжения выражаются в одинаковых единицах:

Значения Е, МПа, для некоторых материалов:

Таблица 1.

Чугун	(1,5... 1,6) 10^5
Сталь	(1,96...2,16) 10^s
Медь	(1,0... 1,3) 10^5
Сплавы алюминия	(0,69... 0,71) 10^5
Дерево (вдоль волокон)	(0,1...0,16) 10^5
Текстолит	(0,06...0,1) ю^5
Капрон	(0,01... 0,02) 10^5

 

Если в формулу закона Гука подставим выражения

 

то получим

Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса.

Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса.

Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать допускаемого:

 

Ориентировочные значения допускаемых напряжений на растяжение и сжатие для некоторых материалов приведены ниже в таблице 2.

Таблица 2.

Материал	[ ], МПа
	Растяжение	сжатие
Чугун серый	28...80	120... 150
Сталь углеродистая конструкционная	60...250
Сталь легированная конструкционная	100...400 и выше
Медь	30... 120
Латунь Бронза	70... 140 60... 120
Дюралюминий	80...150
Текстолит	30...40	50...90
Дуб (вдоль волокна)	9...13	13...15
Кирпичная кладка	до 0,2	0,6...2,5
Бетон	0,1...0,7	1...9

 

Если допускаемые напряжения при растяжении и сжатии различны, то их обозначают соответственно [ _р] и [ _с].

Расчетная формула при растяжении и сжатии имеет вид:

И читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле

не должно превышать допустимое.

При расчете конструкций на прочность встречаются три вида задач, различающихся формой использования расчетной формулы:

1) проектный расчет, при котором определяются размеры опасного сечения по формуле:

2) проверочный расчет, при котором определяется рабочее напряжение и сравнивается с допускаемым по формуле:

3)определение допускаемой нагрузки ведется по формуле

УСЛОВИЯ ЗАДАЧ: №1, №2, №3, №4.

Задача №1.

Стальной ступенчатый брус нагружен системой сосредоточенных сил действующих вдоль оси, как показано на рисунке в задании. Номер задания и варианты исходных данных приведены в таблицах № 2.1. и № 2.5.

Требуется:

· определить продольные силы, напряжения и перемещения поперечных сечений бруса;

· построить эпюры продольных сил, напряжений и перемещений по длине бруса N=f(z), =f(z), = f(z);

· из расчета на прочность определить размеры поперечных сечений каждой ступени, принимая их сплошными круглыми.

Задача №2.

Абсолютно жесткий брус АВ укреплен и поддерживается с помощью трех стержней, как показано на рисунке в задании. Крепление всех стержней — шарнирное. На брус действует сосредоточенная или распределенная нагрузка. Форма поперечного сечения стержней указана на схеме.

Тре буется:

· определить размеры поперечных сечений стержней 1, 2, 3 из условия их равнопрочности. Номер задания и варианты исходных данных приведены в таблицах № 2.2. и № 2.5.

За дач а №3.

Стальной брус нагружен системой сосредоточенных сил и постоянной распределенной нагрузкой, действующих вдоль оси бруса, как показано на рисунке. Номер задания и вариант исходных данных приведены в таблицах № 2.3. и № 2.5.

Требуе тся:

· определить продольные силы, перемещения поперечных сечений бруса;

· построить эпюры продольных сил и перемещений поперечных сечений по длине бруса N = f(z)._:λ = f(z);

· из расчета на прочность определить размеры поперечного сечения, принимая их сплошными круглыми.

Зада ча №4.

Стальной брус нагружен системой сосредоточенных сил и изменяющейся распределенной нагрузкой, действующих вдоль оси бруса, как показано на рисунке в задании. Номер задания и вариант исходных данных приведены в таблицах № 2.4. и № 2.5.

Тре буется:

· определить продольные силы, перемещения поперечных сечений бруса;

· построить эпюры продольных сил N =f (z)и перемещений

λ= f(z)поперечных сечений по длине бруса;

· из расчета на прочность определить размеры поперечного сечения, принимая их сплошными круглыми;

· определить общее перемещение бруса.