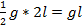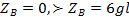Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Сопративление материалов и механика»Содержание книги
Поиск на нашем сайте Кафедра «Сопративление материалов и механика» Печатается по решению научно-методического совета Ташкентского государственного технического университета имени Абу Райхана Беруни. Рецензенты: профессор кафедры «Теория механизмов и деталей машин» ТАДИ, д.т.н.,проф. Ш.П.Алимухамедов доцент кафедры «Сопративление материалов и механика» ТашГТУ, к.т.н.,доц.------------? © Ташкентский государственный технический университет, 2012 ПРЕДИСЛОВИЕ Учебное пособие составлено в соответствии с программой курса «Прикладная механика» для направлений отрасли 520 ООО - «Инженерия и инженерное дело». Программой курса предусматривается чтение лекций, проведение практических и лабораторных занятий, а также самостоятельная работа студентов^ связанная с выполнением расчетно-графических заданий. Настоящее учебное пособие предназначено для обеспечения самостоятельной работы студентов, изучающих дисциплину «Прикладная механика», и оказания им помощи при выполнении расчетно-графических работ: «Расчет брусьев и стержней при растяжении и сжатии», «Расчеты стержней и брусьев на прочность и жесткость при кручении», «Расчет балок на прочность и жесткость при изгибе», «Расчет рамок круглого сечения при растяжении (сжатии) и изгибе». Целью настоящего учебного пособия является закрепление и углубление знаний, полученных студентами при изучении основ сопротивления материалов, являющихся составной частью курса «Прикладная механика». Выполнение работ позволит студентам получить навыки самостоятельного выполнения расчетов на прочность, жесткость стержней и брусьев, элементы которых подвержены растяжению и сжатию, кручению, изгибу. С целью более широкого использования компьютеров при выполнении расчетно-графических работ по сопротивлению материалов, а также для контроля решения некоторых задач использованы результаты совместных научных исследований авторов с учеными Института механики и сейсмостойкости сооружений им. М.Т.Уразбаева по расчету стержневых систем методом конечных элементов на ЭВМ, которые защищены четырьмя свидетельствами на программные продукты Патентного ведомства Республики Узбекистан. При подготовке данного учебного пособия авторами учтен многолетний опыт преподавания курса «Прикладная механика» преподавателями кафедры «Сопративление материалов и механика» ТашГТУ. РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. Сопротивление материалов как наука возникло в эпоху Возрождения, когда развитие техники, торговли, мореплавания, военного дела потребовало научных обоснований, необходимых для постройки крупных морских судов, мостов, гидротехнических сооружений и других сложных конструкций. Основоположником этой науки считают итальянского ученого Галилея (1564-1642). Все элементы сооружений или машин должны работать без угрозы поломки или опасного изменения сечений и формы под действием внешних сил. Размеры этих элементов в большинстве случаев определяют расчет на прочность. Элементы конструкции должны быть не только прочными, но и достаточно жесткими и устойчивыми. Практика показывает, что все части конструкций под действием нагрузок деформируются, т.е. изменяют свою форму и размеры, а в некоторых случаях происходит разрушение конструкции. Принцип Сен-Венана можно сформулировать следующим образом: в точках тела, достаточно удаленных от мест приложения внешних сил, модуль внутренних сил весьма мало зависит от конкретного способа приложения сил. Основные гипотезы и допущения Конструкционные материалы, из которых изготовляют детали машин и сооружений, не являются, строго говоря, непрерывными, однородными во всех точках и изотропными (имеющими одинаковые свойства во всех направлениях). В процессе изготовления заготовок и получения из них готовых деталей в материале появляются различные, не поддающиеся учету поверхностные и внутренние дефекты, например, раковины, трещины и неоднородность структуры в литых деталях, волосовины у штампованных деталей, первоначальные внутренние усилия, вызванные неравномерностью остывания литых и кованых деталей, неравномерностью высыхания и неоднородностью древесины, неравномерностью затвердевания и неоднородностью бетона и т.д. Так как закономерности возникновения указанных явлений установить невозможно, то в сопротивлении материалов принимается ряд гипотез и допущений, которые позволяют исключить из рассмотрения эти явления. В результате объектом изучения в сопротивлении материалов становится не само реальное тело, а его приближенная модель. Экспериментальная проверка выводов, полученных на основании приведенных ниже гипотез и допущений, показывает, что эти выводы вполне пригодны для применения в практике инженерных расчетов. Перейдем к рассмотрению основных гипотез и допущений, касающихся физико-механических свойств материалов. · Гипотеза об отсутствии первоначальных внутренних усилий. Согласно этой гипотезе предполагается, что если нет причин, вызывающих деформацию тела (нагружение, изменение температуры), то во всех его точках внутренние усилия равны нулю. Таким образом, не принимаются во внимание силы взаимодействия между частицами ненагруженного тела. · Допущение об однородности материала. Физико- механические свойства тела могут быть неодинаковыми в разных точках. В сопротивлении материалов этими различиями пренебрегают, полагая, что материал во всех точках теля обладает одинаковыми свойствами. · Допущение о непрерывности материала. Согласно этому допущению, материал любого тела имеет непрерывное строение и представляет собой сплошную среду. Допущение о непрерывном строении материала позволяет применять при расчетах методы высшей математики (дифференциальное и интегральное исчисления). · Допущение об изотропности материала. Это допущение предполагает, что материал тела обладает во всех направлениях одинаковыми свойствами. Многие материалы состоят из кристаллов, у которых физико-механические свойства в различных направлениях существенно различны. Однако, благодаря наличию в теле большого количества беспорядочно расположенных кристаллов, свойства всей массы материала в различных направлениях выравниваются.
Рис. 1.1. Рис. 1.2. Допущение об изотропности хорошо подтверждается практикой для большинства материалов и лишь приближенно для таких материалов, как камень, пластмассы, железобетон. Материалы, имеющие неодинаковые свойства в разных направлениях, называются анизотропными, например, древесина. · Допущение об идеальной упругости. Это допущение предполагает, что в известных пределах нагружение материал обладает идеальной упругостью, т. е. после снятия нагрузки деформации полностью исчезают. Рассмотрим теперь гипотезы и допущения, связанные с деформациями элементов конструкций. Изменение линейных и угловых размеров тела называется соответственно линейной и угловой деформацией. Изменение положения (координат) точек тела, вызванное деформацией, называется перемещением. · Допущение о малости перемещении или принцип начальных размеров. Согласно этому допущению, деформации тела и связанные с ними перемещения точек и сечений весьма малы по сравнению с размерами тела. На основании этого мы будем пренебрегать изменениями в расположении внешних сил, вызванными деформацией. Так, например, не будем принимать во внимание смещение ∆zлинии действия силы F, показанное на рис. 1.1. · Допущение о линейной деформируемости тел. Согласно этому допущению, перемещения точек и сечений упругого тела в известных пределах нагружения прямо пропорциональны силам, вызывающим эти перемещения. · Гипотеза плоских сечений или гипотеза Бернулли. Согласно этой гипотезе, плоские поперечные сечения, проведенные в теле до деформации, остаются при деформации плоскими и нормальными к оси (рис. 1.2.). Эта гипотеза была впервые высказана швейцарским ученым Якобом Бернулли (1654 - 1705) и положена в основу при изучении большинства основных деформаций бруса. К основным гипотезам сопротивления материалов относится также принцип независимости действия сил: результат действия группы сил не зависит от последовательности нагружения или конструкции и равен сумме результатов действия каждой из сил в отдельности, (принцип суперпозиции). Этот принцип применим только для конструкций, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам. РАЗДЕЛ 2. ИСХОДНЫЕ ПОНЯТИЯ. Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила N(z). Брусья с прямолинейной осью (прямые брусья), работающие на растяжение или сжатие, часто называют стержнями. Рассмотрим невесомый, защемленный левым кондом прямой брус, вдоль оси, которого действует активная сила F и 2F (рис. 1.1.). Части бруса постоянного сечения, заключенные между поперечными плоскостями, в которых приложены активные или реактивные силы, будем называть участками. Изображенный на рис. 2.1. брус состоит из двух участков. Применив метод сечений, определим продольные силы N1(z) и N 2 (z) на участках. Рассечем брус на левом участке поперечным сечением 1—1. Во всех точках бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса (например, правой от сечения): Z= 0; 2F- F- N,(z) = О, откуда N,(z) = 2F- F= F. Мы видим, что для равновесия оставленной части бруса в сечении 1 — 1 необходимо приложить только силу Nh направленную вдоль оси, т.е. продольную силу. Продольная сила есть равнодействующая нормальных внутренних сил, возникающих в поперечном сечении бруса. Нетрудно понять, что в сечении 2—2 на правом участке продольная сила будет иметь другое значение: N2(z)~2F. Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса). В дальнейшем растягивающие (направленные от сечения) продольные силы мы будем считать положительными, а сжимающие (направленные к сечению) — отрицательными. При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле:
где N(z)— продольная сила; A— площадь поперечногосечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет.
Рис. 2.1 считать, что во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно. Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635—1703). Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Математический закон Гука можно записать в виде равенства:
Коэффициент пропорциональности Е - характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода. Модуль упругости и напряжения выражаются в одинаковых единицах:
Значения Е, МПа, для некоторых материалов: Таблица 1.
Если в формулу закона Гука подставим выражения
то получим
Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса. Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса. Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать допускаемого:
Ориентировочные значения допускаемых напряжений на растяжение и сжатие для некоторых материалов приведены ниже в таблице 2. Таблица 2.
Если допускаемые напряжения при растяжении и сжатии различны, то их обозначают соответственно [ Расчетная формула при растяжении и сжатии имеет вид:
И читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле
не должно превышать допустимое. При расчете конструкций на прочность встречаются три вида задач, различающихся формой использования расчетной формулы: 1) проектный расчет, при котором определяются размеры опасного сечения по формуле: 2) проверочный расчет, при котором определяется рабочее напряжение и сравнивается с допускаемым по формуле:
3)определение допускаемой нагрузки ведется по формуле
УСЛОВИЯ ЗАДАЧ: №1, №2, №3, №4. Задача №1. Стальной ступенчатый брус нагружен системой сосредоточенных сил действующих вдоль оси, как показано на рисунке в задании. Номер задания и варианты исходных данных приведены в таблицах № 2.1. и № 2.5. Требуется: · определить продольные силы, напряжения и перемещения поперечных сечений бруса; · построить эпюры продольных сил, напряжений и перемещений по длине бруса N=f(z), · из расчета на прочность определить размеры поперечных сечений каждой ступени, принимая их сплошными круглыми. Задача №2. Абсолютно жесткий брус АВ укреплен и поддерживается с помощью трех стержней, как показано на рисунке в задании. Крепление всех стержней — шарнирное. На брус действует сосредоточенная или распределенная нагрузка. Форма поперечного сечения стержней указана на схеме. Тре буется: · определить размеры поперечных сечений стержней 1, 2, 3 из условия их равнопрочности. Номер задания и варианты исходных данных приведены в таблицах № 2.2. и № 2.5. За дач а №3. Стальной брус нагружен системой сосредоточенных сил и постоянной распределенной нагрузкой, действующих вдоль оси бруса, как показано на рисунке. Номер задания и вариант исходных данных приведены в таблицах № 2.3. и № 2.5. Требуе тся: · определить продольные силы, перемещения поперечных сечений бруса; · построить эпюры продольных сил и перемещений поперечных сечений по длине бруса N = f(z).:λ = f(z); · из расчета на прочность определить размеры поперечного сечения, принимая их сплошными круглыми. Зада ча №4. Стальной брус нагружен системой сосредоточенных сил и изменяющейся распределенной нагрузкой, действующих вдоль оси бруса, как показано на рисунке в задании. Номер задания и вариант исходных данных приведены в таблицах № 2.4. и № 2.5. Тре буется: · определить продольные силы, перемещения поперечных сечений бруса; · построить эпюры продольных сил N =f (z)и перемещений λ= f(z)поперечных сечений по длине бруса; · из расчета на прочность определить размеры поперечного сечения, принимая их сплошными круглыми; · определить общее перемещение бруса. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №1. Задача №1. Усло вие: Стальной ступенчатый брус нагружен системой сосредоточенных сил действующих вдоль оси, как показано на рис. 2.2. Требуетс я: · Определить продольные силы, нормальные напряжения и линейные перемещения поперечных сечений бруса. · Построить эпюры продольных сил, напряжений и перемещений N(z); · Из расчёта на прочность определить размеры поперечных сечений каждой ступени, принимая их сплошными, круглыми. Исходные данные: · Нагрузка F = 60 кН; · Длина l=1,2 м; · Допускаемое напряжение [ · Модуль упругости Е = 2 Решение: · Определение продольных сил и построение эпюры N=f(z).Мысленно отбросив опору и заменив ее силой реакции RE, составляем уравнение равновесия для бруса, из которого определяем реакцию в заделке. Реакцию предполагаем растягивающей (рис. 2.2.6). Σ Знак «плюс» обозначает, что предполагаемое направление реакции правильное. Брус имеет три участка. Границами участков служат точки приложения сил. Нумеруем участки. Продольные силы определяем методом сечений. Неизвестную продольную силу в сечении предполагаем растягивающей (рис. 2.2.в).
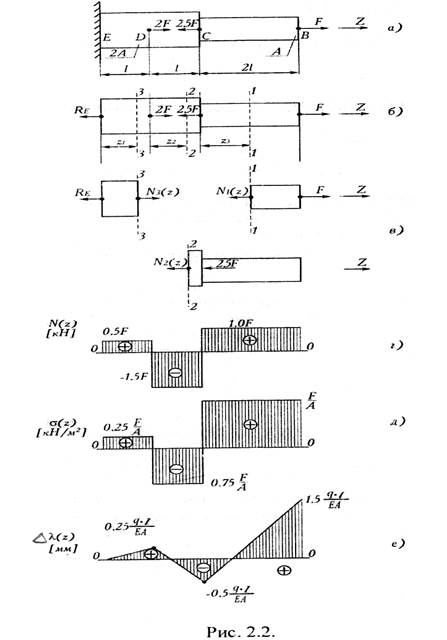
УЧАСТОК, сечение 1-1 ZFiz=0; -N(z)+F=0; N1 (z)=F (растяжения). · УЧАСТОК, сечение 2-2 -N2(z)-2,5F+F=0; N2(z)=F-2,5F=-1.5F (сжатия) · УЧАСТОК, сечение 3-3 -Re+N3(z)=0; N3(z)= Re=0,5F (растяжения). По найденным значениям строим эпюру продольных сил, т.е. график N(z). При этом принимают определенный масштаб, как по длине бруса, так и для ординат. На рисунке 1(г) одна единица длины l принята 25 мм, а единица силы F-10мм. 2. Определение напряжений и построение эпюры σ (z). Поскольку продольные силы на участках постоянные, но и нормальные напряжения в любом сечении участка будут одинаковы. Напомним, что при осевом растяжении или сжатии в самом поперечном сечении нормальные напряжения распределены равномерно. · УЧАСТОК σ1 (z) =N1 (z)/А1=F/A; · УЧАСТОК σ2 (z)= N2(z)/A2=-1,5F/2A=-0,75F/A; · УЧАСТОК σ3(z)=N3(z)/A3=0,5F/2A= 0,25F/A; По найденным значениям строим эпюру (рис. 1.д). При этом принимаем определенный масштаб для напряжений. Например, одна единица напряжения F/A принята равной 20 мм на чертеже. 3. Определение перемещения поперечных сечений и построения эпюры λ(z). Определим перемещения характерных сечений, т.е. сечений на границах участков В, С, D, Е.. Сразу же отметим, что перемещение сечения Е (заделки) равно нулю. ∆λ(z)=0 Перемещение остальных точек удобно определить го отношению к неподвижному сечению. ∆λЕ(z)=0 3 УЧАСТОК: 0≤Z3≤ l ; ∆λD(z)=λE(z)+∆l3(z)=0+N3(z)·Z3/E·A3=0,5F·Z3/E·2A=0,25F·Z3/E·A При постоянных продольных силах перемещения линейно зависят от расстояния. Поэтому достаточно вычислить перемещения в двух точках в начале и конце участка. ∆λD(Z3=0)=0 ∆λD(Z3=l)=0,25F·l/EA; 2 УЧАСТОК: 0≤Z2≤l; ∆λC(z)=∆λD(z=l)+∆l2(z)=0,25F·l/EA+N2(z)·Z2/E·A2=0,25F·l/EA+1,5F·Z/E·2A; ∆λC(0)=0,25F·l/EA; ∆λC(l)=-0,5F·l/EA; 1 УЧАСТОК: 0≤ Z1 ≤2l; ∆λB(z)=∆λC(l)+∆l1(z)=-0,5F·l/EA+N1(z)·Z1/E·A1=-0,5F·l/Ea+F·Z1/E·A; ∆λB(0)=-0,5F·l/EA; ∆λ(2l)=-0,5F·l/EA+F·2l/EA=1,5F·l/EA; По этим данным строим эпюру ∆λ(Z ), причём для ординат ∆λ(Z) принят также определённый масштаб. На рис. 2.2. е одна единица перемещения F ·l/EA принята равным 25 мм на чертеже. Эпюры ∆λ(Z ) используются в расчетах на жесткость. Вычисляем перемещение свободного конца бруса: ∆λB(z)= 1,5F·l/EA=1,5 (60-1,2)/(2·103·430) =54/(43·106) где площадь поперечного сечения принята А=430 мм2. 4. Определение размеров поперечного сечение бруса. По эпюре напряжения (рисЛ.д) видно, что наибольшие напряжения возникают на первом участке, причем все сечения здесь рав- ноопасны. Запишем условие прочности для первого участка: σmax≤[σ]; F/A≤[σ] Из условия прочности определяем площади поперечных сечений бруса и их диаметры. A≥F[σ]60·103/140=428,5мм2 принимаем А=430мм2.
A1=A=430 мм2
d1=
d2=
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №2. Задача №2. У словие: Абсолютно жесткий брус АВ укреплен в точке В шарнирно к стене, а в точке А с помощью трех стержней подвешен к верх- Нл'й опоре (рис 2.3.а). Крепления всех стержней шарнирные. Поперечные сечения стержней указаны на рисунке. На брус АВ действует равномерно распределенная нагрузка интенсивностью q. Требуется: 1. Определить размеры поперечных сечений стержней 1, 2, 3, на условиях их равнопрочности. Исходные данные: - Интенсивность распределенной нагрузки q= 50кН/м - Длина I = 1,2 м Углы стержней в системе - - - Допускаемое напряжение для материала стержней Е=2*
Решение. 1. Рассмотрим равновесие абсолютно жесткого бруса АВ. Для этого отбросим связи и заменим их силами реакций. В точке В имеем две составляющие реакции, а в точке А реакция направлена по стержню 1 (рис2.2.б). Таким образом, на брус действует плоская система сил N,, Вх,Ву,2ql, для которой можно составить три уравнения равновесия. Этих уравнений достаточно для определения трех неизвестных усилий.
1.
2.
3.
В связи с тем, что в задаче не требуется определить реакцию в шарнире В, для определения усилия в стержне 1 достаточно воспользоваться одним уравнением моментов относительно точки В, из которого:
2.Рассмотрим равновесие точки О. Для чего также освободим ее от связей, а вместо них приложим силы реакций (рис 2.2.в). Точка О находится, в равновесии под действием трех сходящихся сил Nj, N2, N3. Для такой системы можно составить два уравнения равновесия, что будет достаточно для определения усилий N2, N3. Выбираем систему координат. Так как углы<р, и ср2 в сумме составляют 90°, то удобно оси X и Yнаправить по направлению усилий N2и N3.
Откуда:
3. Используя условия прочности, определяем площади поперечных сечений стержней 1, 2, 3 и их размеры: σ=
a)
Рис. 2.3.
2.6. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №3.
Задача №3. Условие: Стальной стержень с постоянной жесткостью EA-c.onst. нагружен системой сосредоточенных сил и распределенной, действующей вдоль оси, нагрузкой (рис. 2.4.). Требуется: 1. Определить и построить эпюры продольной силы N(z)линейного перемещения A(z).Из расчета на прочность определить размеры поперечного сечения стержня, принимая его круглым. 2. Определить полную деформацию.
Ч Дано: - q=45 кН, - 1=1,5 м, Е=2 105 мПа. - Найти: N(z), A(z).:Abe(z), d=? Рис. 2.4 Решение: Для решения данной задачи применим метод сечений, но сначала определим реакцию опоры ZBиз уравнения: -ql — 3ql- 3ql+ 2ql + ZB= 0, ZB=5ql. Разделим тело на три участка — ВС - первый, CD- второй, DE- третий. На каждом из участков проведем сечение перпендикулярное оси z.
Отбрасываем левую часть участка, при этом в сечении возникает внутренняя продольная сила N1(z1), где 0 ≤ z1 ≤ l. Определим N1(z1) -
Рассмотрим второй участок CD:
Отбрасываем левую часть участка, при этом в сечении возникает внутренняя продольная сила N2(z2), где 0 <z2< I. ОпределимN2(z2) -
Рассмотрим третий участок DE:
Отбрасываем правую часть участка, при этом в сечении возникает внутренняя продольная сила N3(z.3), где 0<z3</- Определим N3(z3)-ql-qz3=0 N3(z3) =ql + qz3 N3(o)=ql N3(l)=ql +ql = 2ql Определим удлинение стержня: Для этого примем удлинение точки В равным нулю, то есть Хв=0, тогда удлинение точки С можно представить в виде:
=
Удлинение точки D:
Определим диаметр поперечного сечения: Условие прочности при растяжении и сжатии: (Timx (z) < -——— < [<т], где А площадь поперечного сечения А
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №4 Задача №4 Условие: Стальной стержень с постоянной жесткостью EA=const. нагружен системой сосредоточенныхcwiи распределенной действующей вдоль оси, нагрузкой (рис. 2.6.). Треб уе тся: 1. Определить и построить эпюры продольной силы N(z)линейного перемещения X(z).Из расчета на прочность определить размеры поперечного сечения стержня, принимая его круглым. Определить полную деформацию
Дано: - q = 45 кН, - I = 1.5 м, Е = 210sмПа. - [аст] = 140 мПа. Найти: N(z), Mz), AfJz),d=?
Решение: Для решения данной задачи применим метод сечений, но сначала определим результирующую силу Gраспределенной нагрузки: G= Определим реакцию опоры ZBиз уравнения: 7gl-gl- Разделим тело на два участка – ВС – первый, СD – второй. На каждой из участков проведем сечение перпендикулярное оси z. РАЗДЕЛ 3. «РАСЧЕТ БРУСЬЕВ И СТЕРЖНЕЙ ПРИ КРУЧЕНИИ» 3.1. ИСХОДНЫЕ понятия. Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент. Деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных оси, приложить пары сил. Момент этих пар будем называть вращающими. Вращающий момент обозначается Т. Относительным углом закручивания φ0 называется отношение угла закручивания φ z расстоянию z данного сечения от заделки. Если брус длиной I имеет постоянное сечение и нагружен скручивающим моментом на конце (т.е. состоит из одного участка), то
Крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения. Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение, то опасным будут сечения на участке, где возникает наибольший крутящий момент. Крутящий момент полагаем положительным, если при взгляде со стороны сечения результирующий момент внешних пар, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот. Условие прочности бруса при кручении заключается в том, что наибольшее возникающее в нем касательное напряжение не должно превышать допускаемое. Расчетная формула на прочность при кручении имеет вид τ=Mk /Wp </ τк] и читается так: касательное напряжение в опасном сечении, вычисленное по формуле τ=Mk /Wp, не должно превышать допускаемое. Допускаемое напряжение при кручении выбирают в зависимости от допускаемого напряжения при растяжении, а именно: для сталей [τk] = 0,55…0,60)/σр]; для чугунов [τk] = 1…1,2)/σр] Кроме прочности к валам предъявляется требование жесткости, заключающееся в том, что угол закручивания 1 м длины вала не должен превышать определенной величины во избежание, например, пружинения валов или потери точности ходовых винтов токарно-винторезных станков. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0]; расчетная формула на жесткость при кручении имеет вид
Величины допускаемых углов закручивания зависят от назначения вала; их обычно принимают в следующих пределах: [φo]= 0,25... 1 град/м. С помощью выведенных расчетных формул выполняются три вида расчетов конструкций на прочность и жесткость при кручении — проектный, проверочный и определение допускаемой нагрузки.
3.2. УСЛОВИЯ ЗАДАЧ №5, №6. Задача №5. Стальной ступенчатый брус круглого поперечного сечения нагружен парами сил, действующими перпендикулярно оси, как показано на рисунке в задании. Номер задания и варианты исходных данных приведены в таблицах N° 3.1. и № 3.3.
-определить крутящие моменты по участкам и построить эпюру крутящих моментов; - из условия прочности определить диаметр каждой ступени; -определить углы закручивания поперечных сечений бруса и построить эпюру φ = (z). Задача №6. Стальная балка круглого поперечного сечения нагружена парами сил, действующими перпендикулярно оси, как показано на рисунке в задании. Номер задания и варианты исходных данных пр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |




 В сечениях, близких к точкам приложения растягивающих или сжимающих сил, закон распределения напряжений по сечению будет более сложным, но, пользуясь принципом смягченных граничных условий, мы будем этими отклонениями пренебрегать и
В сечениях, близких к точкам приложения растягивающих или сжимающих сил, закон распределения напряжений по сечению будет более сложным, но, пользуясь принципом смягченных граничных условий, мы будем этими отклонениями пренебрегать и







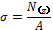






 =
=  =23,4мм
=23,4мм 
 =
=  =33мм
=33мм

 мм
мм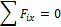



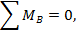

 kH
kH



 =82,1kH
=82,1kH

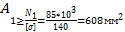 a=24,2мм
a=24,2мм d=14,2мм
d=14,2мм 40X40X4(по ГОСТ8239-72)
40X40X4(по ГОСТ8239-72)


 -
-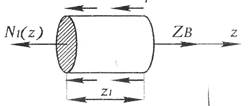 Рассмотрим первый участок ВС:
Рассмотрим первый участок ВС:

 =5gl
=5gl

 +2gl+
+2gl+  =0
=0

 =5gl;
=5gl; =0+
=0+  =
=  =
= 0;
0; 
 =6,1
=6,1  *(-gl
*(-gl 
 ;
;