
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим первый участок ВС.Содержание книги
Поиск на нашем сайте
Отбрасываем правую часть участка, при этом в сечении, возникает внутренняя продольная сила N,(z]),где 0<z, </. Определим N i(zi)
Определим g( g(
Тогда
Рассмотрим второй участок CD: Отбрасываем левую часть участка, при этом в сечении возникает внутренняя продольная сила N2(z2), где 0<z2</. Определим N2(z2)
Тогда:
Определим удлинение стержня: Для этого примем удлинение точки В равным нулю, то есть
= Удлинение точки D:
То есть:
Полная деформация стержня равна
РАЗДЕЛ 3. «РАСЧЕТ БРУСЬЕВ И СТЕРЖНЕЙ ПРИ КРУЧЕНИИ» 3.1. ИСХОДНЫЕ понятия. Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент. Деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных оси, приложить пары сил. Момент этих пар будем называть вращающими. Вращающий момент обозначается Т. Относительным углом закручивания φ0 называется отношение угла закручивания φ z расстоянию z данного сечения от заделки. Если брус длиной I имеет постоянное сечение и нагружен скручивающим моментом на конце (т.е. состоит из одного участка), то
Крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения. Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение, то опасным будут сечения на участке, где возникает наибольший крутящий момент. Крутящий момент полагаем положительным, если при взгляде со стороны сечения результирующий момент внешних пар, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот. Условие прочности бруса при кручении заключается в том, что наибольшее возникающее в нем касательное напряжение не должно превышать допускаемое. Расчетная формула на прочность при кручении имеет вид τ=Mk /Wp </ τк] и читается так: касательное напряжение в опасном сечении, вычисленное по формуле τ=Mk /Wp, не должно превышать допускаемое. Допускаемое напряжение при кручении выбирают в зависимости от допускаемого напряжения при растяжении, а именно: для сталей [τk] = 0,55…0,60)/σр]; для чугунов [τk] = 1…1,2)/σр] Кроме прочности к валам предъявляется требование жесткости, заключающееся в том, что угол закручивания 1 м длины вала не должен превышать определенной величины во избежание, например, пружинения валов или потери точности ходовых винтов токарно-винторезных станков. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0]; расчетная формула на жесткость при кручении имеет вид
Величины допускаемых углов закручивания зависят от назначения вала; их обычно принимают в следующих пределах: [φo]= 0,25... 1 град/м. С помощью выведенных расчетных формул выполняются три вида расчетов конструкций на прочность и жесткость при кручении — проектный, проверочный и определение допускаемой нагрузки.
3.2. УСЛОВИЯ ЗАДАЧ №5, №6. Задача №5. Стальной ступенчатый брус круглого поперечного сечения нагружен парами сил, действующими перпендикулярно оси, как показано на рисунке в задании. Номер задания и варианты исходных данных приведены в таблицах N° 3.1. и № 3.3.
-определить крутящие моменты по участкам и построить эпюру крутящих моментов; - из условия прочности определить диаметр каждой ступени; -определить углы закручивания поперечных сечений бруса и построить эпюру φ = (z). Задача №6. Стальная балка круглого поперечного сечения нагружена парами сил, действующими перпендикулярно оси, как показано на рисунке в задании. Номер задания и варианты исходных данных приведены в таблицах N° 3.2. и № 3.3. Требуется: 1- определить крутящие моменты по участкам и построить эпюру крутящих моментов; 2- определить углы закручивания поперечных сечений бруса и построить эпюру ∆φ(z) 3- из условия прочности определить диаметр поперечного сечения балки; 4- определить полное закручивание вала. 3.3. СИСТЕМА ЕДИНИЦ И ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ. В методическом указании используется международная система единиц СИ. Обозначение величин: 1- Система координат — правая, продольная ось — Z, оси в поперечном сечении — X, Y. 2- Нагрузка, внешняя сила — F. 3- Внешний вращающий момент (пара сил) — т. 4- Внутренние силовые факторы: продольная сила —N(z), поперечные силы — Qx, Qy; изгибающие моменты — Мх, Mv; крутящий момент — Т. 5- Моменты инерции плоского сечения: осевой, полярный, центробежный — 1Х; 1у, 1р. 6- Моменты сопротивления осевые, полярный — Wx, Wy, Wp 7- Касательное напряжение — Т. 8- Допускаемое номинальное напряжение нормальное, касательное — [а], [г] 9- Модуль сдвига — G. 10- Жесткость при кручении, при изгибе — GIp, GIX 11- Угол закручивания бруса — ф 12- Вертикальное перемещение поперечного сечения — V 13- Угол поворота поперечного сечения бсиши — О
Таблица 3.3. ИСХОДНЫЕ ДАННЫЕ К ЗАДАЧАМ.
3.4. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №5. Задача №5. Условия: Стальной ступенчатый брус нагружен парами сил, действующими перпендикулярно оси бруса, как показано на рис. 3.1.а. Требу ется: 1-Определить крутящие моменты по участкам и построить эпюру крутящих моментов T(z). 2-Из условия прочности определить диаметры поперечных сечений каждой ступени. 3-Определить углы закручивания поперечных сечений бруса и построить эпюру <p(z). Ис ход н ые данные: -Нагрузки т=5кНм -Длина 1=0,4м -Допускаемое касательное напряжение [т]=70МПа -Модуль упругости G-8104МПа Решение. 1. Определение крутящих моментов и построение эпюру T(z). Для определения реакции опори в т А мысленно отбросим опору и заменим ее реактивным моментом. Затем составляем уравнение равновесия для всего бруса, из которого определяем момент в заделке. Вращение заданных пар сил действующих на брус рассматриваем стоя лицом к свободному концу бруса
Знак «плюс» обозначает, что предполагаемое направление реактивного момента выбрано, верно. Для определения T(z) - крутящих моментов нумерация участков можно начинать как справа, так и слева бруса. Наши деление бруса на участки и сечения сделано слева направо. Крутящий момент определяется методом сечение. Неизвестный крутящий момент 14- УЧАСТОК: О T(z)= - M =- 4 m (const.)- (слева рассматриваем, стоя лицом к сечению). 15- УЧАСТОК: 0 T(z)= - M+3 m= - 4 m+3 m = - m - (const.)- (слева рассматриваем, стоя лицом к сечению). 16- УЧАСТОК: 2/<Z3< О T(z)= m - (const.)- (рассматриваем справа, стоя лицом к сечению). По данным строим эпюру T(z) (рис 3.1.г.). Принимаем масштаб l=25мм в единицу крутящего момента т=7мм. 2.Размеры поперечных сечений определяем из условия прочности при кручении.
на 1-участке
Принимаем d1=115мм. На 3-участке: \T(z)\ = т
Принимаем d3=72мм.
3. Определение углов закручивания поперечных сечений бруса и построение эпюра 1-УЧАСТОК: О
2-УЧАСТ0К: 0
- линейный закон;
3-УЧАСТОК: 0
Ha 3-участке найдено соотношение полярных моментов инерции поперечных сечений 1 и 2 - участков:
Jp3=Jp1 По этим данным построены эпюры Эпюра Вычисляем угол закручивания свободного конца бруса: 3.5. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №6.,
Задача №6. Ус ловия: Для заданной стальной балки Рис. 3.3.
Т реб уе тся: 17- Определить и построить эпюры Т — крутящего момента. 18- Из условий прочности определить диаметр поперечного сечения. 19- Определить угол закручивания и построить его эпюры. 20- Определить полное закручивание вала.
Дано: 21- т=7 кНм, 22- l=1,5 м, Е=2 105 мПа. 23- [ 24- G= 8104 мПа. Найти: T(z), Решение: Для решения данной задачи применим метод сечений, но сначала определим реакцию опоры тА из следующего уравнения: 2 т-т-М А =0 МА = т. Разделим тело на два участка — АВ - первый, ВС - второй. На каждом из участков проведем сечение перпендикулярное оси z. Р ассмотрим первый участок АВ:
Отбрасываем левую часть участка, при этом в сечении возникает крутящийся момент T1(z),где 0 T1(z1)+
Рассмотрим второй участок ВС: Отбрасываем правую часть участка, при этом в сечении возникает крутящийся момент T2(z2),где 0 T2(z2) + m= 0, T2(z2) = -m T1(0)=-m, Т1(2l)= -т. Определим угол закручивания , для этого примем закручивание точки А равным нулю, то есть
Так T1(z1)на участке АВ меняет знак с положительного на отрицательный, то в точке T1(zэкстр) =0 угол закручивания достигает экстремального значения, и для того чтобы определить это экстремальное значение угла закручивания решим уравнение: m- zэкстр= Тогда экстремальное значение угла закручивания будет равно:
Определим угол закручивания для точки С:
Полное закручивание тогда будет равно:
Из условий прочности определим диаметр:
РАЗДЕЛ 4. "РАСЧЁТ БРУСЬЕВ И СТЕРЖНЕЙ ПРИ ИЗГИБЕ" ИСХОДНЫЕ ПОНЯТИЯ. Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент. Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным. Изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести всех внешних сил, действующих справа или слева от сечения. У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т.е. система параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно, сумма внешних сил, действующих на балку левее сечения, численно равна сумме сил, действующих на балку правее сечения. Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечений. Так как правило, знаков статики неприемлемо для установления знаков изгибающего момента и поперечной силы, то установим для них другие правила знаков, а именно: -если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот (рис. 1);
Рис. 4.1. Рис. 4.2.
- если сумма внешних сил, лежащих на левую сторону от сечения, дает равнодействующую, направленную вверх,то попе Правило знаков для изгибающих моментов иногда называют «правилом дождя» (имея в виду, что в случае выпуклости вниз образуется воронка, в которой задержится дождевая вода, и наоборот). Условие прочности балки при изгибе заключается в том, что нормальное максимальное напряжение в опасном сечении не должно превосходить допускаемое. Полагая, что гипотеза о ненадавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения в поперечном сечении вычислять при поперечном изгибе по той же формуле, что и при чистом изгибе. Расчетная формула на прочность при изгибе имеет вид
и читается так: нормальное напряжение в опасном сечении,вычисленное по формуле Максимальный изгибающий момент определяют из эпюр изгибающих моментов или расчетом. Так как момент сопротивления изгибу W расчетной формуле стоит в знаменателе, то чем больше W, тем меньше будут расчетные напряжения. Определим моменты сопротивления изгибу наиболее распространенных сечений: 1. Прямоугольник b*h (рис. 4.3.):
Если балку прямоугольного сечения положить плашмя, то
следовательно, при прочих равных условиях нормальные максимальные напряжения Из сказанного следует правило: для обеспечения максимальной прочности ось, относительно которой момент инерции максимален, должна быть нейтральной. 2.Круг диаметром d:
3.Круг размером Dх d:
Момент сопротивления кольцевого сечения нельзя вычислять как разность моментов сопротивлений большого и малого кругов. Нетрудно подсчитать, что при одинаковой площади поперечного сечения, т.е. одинаковом расходе материала, момент сопротивления кольцевого сечения больше момента сопротивления сплошного круглого сечения.
Так как вблизи нейтральной оси материал мало напряжен, то выгодно больше материала располагать дальше от нейтральной оси. Поэтому в машиностроении редко применяют металлические балки прямоугольного сечения, но весьма широко распространены прокатные профильные балки таврового, двутаврового, углового, швеллерного и других сечений. Моменты инерции, моменты сопротивления и другие сведения о прокатных фасонных профилях стандартных размеров даются в таблицах ГОСТа. Для балок, материал которых неодинаково работает на растяжение и сжатие (например, чугун), целесообразно применять профили, не симметричные относительно нейтральной оси, например, тавровый или П-образный. Так как у несимметричного профиля при изгибе возникают неодинаковые напряжения растяжения и сжатия, то сечение, например, чугунной балки выгодно располагать так, чтобы меньшие напряжения были в зоне растянутых, а большие — в зоне сжатых волокон. УСЛОВИЯ ЗАДАЧ №7, №8. Задача №7. Для заданной стальной балки, закрепленной жестко одним концом и нагруженной, как показано на схеме в задании. Номер задания и варианты исходных данных приведены в таблицах № 4.1м №4.3. Требуется - Определить внутренние силовые факторы (поперечные силы и изгибающие моменты) и построить эпюры Q и Мx. - Из условия прочности определить размеры поперечного сечения бруса в двух вариантах: а) Сечение двутавровое. б) Сечение прямоугольное Зада ча №8. Для заданной стальной балки на двух опорах нагруженной, как показано на схеме в задании. Номер задания и варианты исходных данных приведеys в таблицах № 4.2. и № 4.3. Тре бует ся: - Определить внутренние силовые факторы (поперечные силы и изгибающие моменты) и построить эпюры Qи Мх. - Из условия прочности определить размеры поперечного сечения бруса в двух вариантах: а) Сечение двутавровое. б) Сечение прямоугольное (h=
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


 -
- 

 =
= 
 из соотношения (из подобия треугольников):
из соотношения (из подобия треугольников): ≻ g(
≻ g(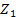 )=
)= 
 6gl+
6gl+ 




 , ≻ g(
, ≻ g(
 и
и
 =0, тогда удлинение точки С можно представить в виде:
=0, тогда удлинение точки С можно представить в виде:
 =6,1
=6,1 
 +
+  =6,1
=6,1  =6,1
=6,1 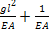 *(-gl
*(-gl 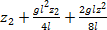 +
+ 


 Определим диаметр поперечного сечения из условия прочности при растяжении и сжатии:
Определим диаметр поперечного сечения из условия прочности при растяжении и сжатии:
 Выбираем d=32 мм, по стандартному ряду.
Выбираем d=32 мм, по стандартному ряду.








 MB-3 m-2т+ т=0: MB=4m
MB-3 m-2т+ т=0: MB=4m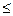 Z1
Z1 
 Wp=
Wp= 

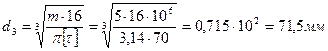

 . Углы закручивания поперечного сечения бруса начинаем рассматривать с неподвижной опоры в т
. Углы закручивания поперечного сечения бруса начинаем рассматривать с неподвижной опоры в т  (z)=0.
(z)=0.
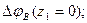

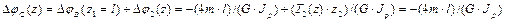



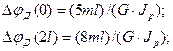


 - принята 4мм на чертеже.
- принята 4мм на чертеже. (z) - используется в расчетах на жесткость.
(z) - используется в расчетах на жесткость.
 ] = 80 мПа.
] = 80 мПа.
 ? Рис. 3.3.
? Рис. 3.3. ,который всегда направлен, независимо от действия внешних сил, против часов, то есть всегда положителен. Определим T1(z1), из следующего уравнения:
,который всегда направлен, независимо от действия внешних сил, против часов, то есть всегда положителен. Определим T1(z1), из следующего уравнения:


 , который всегда направлен, независимо от действия внешних сил, против часов, то есть всегда положителен. Определим T2(z2), из следующего уравнения:
, который всегда направлен, независимо от действия внешних сил, против часов, то есть всегда положителен. Определим T2(z2), из следующего уравнения:
 , откуда
, откуда



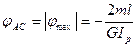 i
i , где Wp— полярный момент сопротивления,
, где Wp— полярный момент сопротивления,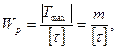



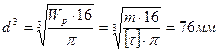



 не должно превышать допускаемое. Допускаемое нормальное напряжение при изгибе выбирают таким же, как и при растяжении и сжатии.
не должно превышать допускаемое. Допускаемое нормальное напряжение при изгибе выбирают таким же, как и при растяжении и сжатии.
 ,тогда
,тогда
 ' у прямоугольной балки, положенной плашмя, будут больше, чем у той же балки, когда ее габаритный наибольший размер h вертикален (имеется в виду, что изгиб происходит в вертикальной плоскости).
' у прямоугольной балки, положенной плашмя, будут больше, чем у той же балки, когда ее габаритный наибольший размер h вертикален (имеется в виду, что изгиб происходит в вертикальной плоскости).



 ), круглое или квадратное по указанию преподавателя.
), круглое или квадратное по указанию преподавателя.


