Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система единиц и принятые обозначения.Содержание книги
Поиск на нашем сайте В методическом указании используется международная система единиц СИ. Обозначение величин: · Система координат — правая, продольная ось — Z, оси в поперечном сечении — X, Y. · Нагрузка, внешняя сила — F. · Площадь поперечного сечения — А. · Внутренняя продольная сила— N(z). · Нормальное напряжение — · Допускаемое номинальное напряжение — [ · Модуль упругости первого рода — Е. · Жесткость бруса — ЕА. · Линейное перемещение поперечного сечения — λ(z).
Таблица 2.5. ИСХОДНЫЕ ДАННЫЕ К ЗАДАЧАМ
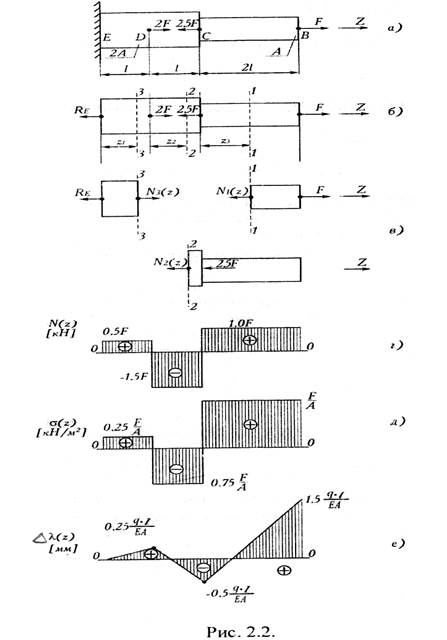
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №1. Задача №1. Усло вие: Стальной ступенчатый брус нагружен системой сосредоточенных сил действующих вдоль оси, как показано на рис. 2.2. Требуетс я: · Определить продольные силы, нормальные напряжения и линейные перемещения поперечных сечений бруса. · Построить эпюры продольных сил, напряжений и перемещений N(z); · Из расчёта на прочность определить размеры поперечных сечений каждой ступени, принимая их сплошными, круглыми. Исходные данные: · Нагрузка F = 60 кН; · Длина l=1,2 м; · Допускаемое напряжение [ · Модуль упругости Е = 2 Решение: · Определение продольных сил и построение эпюры N=f(z).Мысленно отбросив опору и заменив ее силой реакции RE, составляем уравнение равновесия для бруса, из которого определяем реакцию в заделке. Реакцию предполагаем растягивающей (рис. 2.2.6). Σ Знак «плюс» обозначает, что предполагаемое направление реакции правильное. Брус имеет три участка. Границами участков служат точки приложения сил. Нумеруем участки. Продольные силы определяем методом сечений. Неизвестную продольную силу в сечении предполагаем растягивающей (рис. 2.2.в).
УЧАСТОК, сечение 1-1 ZFiz=0; -N(z)+F=0; N1 (z)=F (растяжения). · УЧАСТОК, сечение 2-2 -N2(z)-2,5F+F=0; N2(z)=F-2,5F=-1.5F (сжатия) · УЧАСТОК, сечение 3-3 -Re+N3(z)=0; N3(z)= Re=0,5F (растяжения). По найденным значениям строим эпюру продольных сил, т.е. график N(z). При этом принимают определенный масштаб, как по длине бруса, так и для ординат. На рисунке 1(г) одна единица длины l принята 25 мм, а единица силы F-10мм. 2. Определение напряжений и построение эпюры σ (z). Поскольку продольные силы на участках постоянные, но и нормальные напряжения в любом сечении участка будут одинаковы. Напомним, что при осевом растяжении или сжатии в самом поперечном сечении нормальные напряжения распределены равномерно. · УЧАСТОК σ1 (z) =N1 (z)/А1=F/A; · УЧАСТОК σ2 (z)= N2(z)/A2=-1,5F/2A=-0,75F/A; · УЧАСТОК σ3(z)=N3(z)/A3=0,5F/2A= 0,25F/A; По найденным значениям строим эпюру (рис. 1.д). При этом принимаем определенный масштаб для напряжений. Например, одна единица напряжения F/A принята равной 20 мм на чертеже. 3. Определение перемещения поперечных сечений и построения эпюры λ(z). Определим перемещения характерных сечений, т.е. сечений на границах участков В, С, D, Е.. Сразу же отметим, что перемещение сечения Е (заделки) равно нулю. ∆λ(z)=0 Перемещение остальных точек удобно определить го отношению к неподвижному сечению. ∆λЕ(z)=0 3 УЧАСТОК: 0≤Z3≤ l ; ∆λD(z)=λE(z)+∆l3(z)=0+N3(z)·Z3/E·A3=0,5F·Z3/E·2A=0,25F·Z3/E·A При постоянных продольных силах перемещения линейно зависят от расстояния. Поэтому достаточно вычислить перемещения в двух точках в начале и конце участка. ∆λD(Z3=0)=0 ∆λD(Z3=l)=0,25F·l/EA; 2 УЧАСТОК: 0≤Z2≤l; ∆λC(z)=∆λD(z=l)+∆l2(z)=0,25F·l/EA+N2(z)·Z2/E·A2=0,25F·l/EA+1,5F·Z/E·2A; ∆λC(0)=0,25F·l/EA; ∆λC(l)=-0,5F·l/EA; 1 УЧАСТОК: 0≤ Z1 ≤2l; ∆λB(z)=∆λC(l)+∆l1(z)=-0,5F·l/EA+N1(z)·Z1/E·A1=-0,5F·l/Ea+F·Z1/E·A; ∆λB(0)=-0,5F·l/EA; ∆λ(2l)=-0,5F·l/EA+F·2l/EA=1,5F·l/EA; По этим данным строим эпюру ∆λ(Z ), причём для ординат ∆λ(Z) принят также определённый масштаб. На рис. 2.2. е одна единица перемещения F ·l/EA принята равным 25 мм на чертеже. Эпюры ∆λ(Z ) используются в расчетах на жесткость. Вычисляем перемещение свободного конца бруса: ∆λB(z)= 1,5F·l/EA=1,5 (60-1,2)/(2·103·430) =54/(43·106) где площадь поперечного сечения принята А=430 мм2. 4. Определение размеров поперечного сечение бруса. По эпюре напряжения (рисЛ.д) видно, что наибольшие напряжения возникают на первом участке, причем все сечения здесь рав- ноопасны. Запишем условие прочности для первого участка: σmax≤[σ]; F/A≤[σ] Из условия прочности определяем площади поперечных сечений бруса и их диаметры. A≥F[σ]60·103/140=428,5мм2 принимаем А=430мм2.
A1=A=430 мм2
d1=
d2=
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №2. Задача №2. У словие: Абсолютно жесткий брус АВ укреплен в точке В шарнирно к стене, а в точке А с помощью трех стержней подвешен к верх- Нл'й опоре (рис 2.3.а). Крепления всех стержней шарнирные. Поперечные сечения стержней указаны на рисунке. На брус АВ действует равномерно распределенная нагрузка интенсивностью q. Требуется: 1. Определить размеры поперечных сечений стержней 1, 2, 3, на условиях их равнопрочности. Исходные данные: - Интенсивность распределенной нагрузки q= 50кН/м - Длина I = 1,2 м Углы стержней в системе - - - Допускаемое напряжение для материала стержней Е=2*
Решение. 1. Рассмотрим равновесие абсолютно жесткого бруса АВ. Для этого отбросим связи и заменим их силами реакций. В точке В имеем две составляющие реакции, а в точке А реакция направлена по стержню 1 (рис2.2.б). Таким образом, на брус действует плоская система сил N,, Вх,Ву,2ql, для которой можно составить три уравнения равновесия. Этих уравнений достаточно для определения трех неизвестных усилий.
1.
2.
3.
В связи с тем, что в задаче не требуется определить реакцию в шарнире В, для определения усилия в стержне 1 достаточно воспользоваться одним уравнением моментов относительно точки В, из которого:
2.Рассмотрим равновесие точки О. Для чего также освободим ее от связей, а вместо них приложим силы реакций (рис 2.2.в). Точка О находится, в равновесии под действием трех сходящихся сил Nj, N2, N3. Для такой системы можно составить два уравнения равновесия, что будет достаточно для определения усилий N2, N3. Выбираем систему координат. Так как углы<р, и ср2 в сумме составляют 90°, то удобно оси X и Yнаправить по направлению усилий N2и N3.
Откуда:
3. Используя условия прочности, определяем площади поперечных сечений стержней 1, 2, 3 и их размеры: σ=
a)
Рис. 2.3.
2.6. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №3.
Задача №3. Условие: Стальной стержень с постоянной жесткостью EA-c.onst. нагружен системой сосредоточенных сил и распределенной, действующей вдоль оси, нагрузкой (рис. 2.4.). Требуется: 1. Определить и построить эпюры продольной силы N(z)линейного перемещения A(z).Из расчета на прочность определить размеры поперечного сечения стержня, принимая его круглым. 2. Определить полную деформацию.
Ч Дано: - q=45 кН, - 1=1,5 м, Е=2 105 мПа. - Найти: N(z), A(z).:Abe(z), d=? Рис. 2.4 Решение: Для решения данной задачи применим метод сечений, но сначала определим реакцию опоры ZBиз уравнения: -ql — 3ql- 3ql+ 2ql + ZB= 0, ZB=5ql. Разделим тело на три участка — ВС - первый, CD- второй, DE- третий. На каждом из участков проведем сечение перпендикулярное оси z.
Отбрасываем левую часть участка, при этом в сечении возникает внутренняя продольная сила N1(z1), где 0 ≤ z1 ≤ l. Определим N1(z1) -
Рассмотрим второй участок CD:
Отбрасываем левую часть участка, при этом в сечении возникает внутренняя продольная сила N2(z2), где 0 <z2< I. ОпределимN2(z2) -
Рассмотрим третий участок DE:
Отбрасываем правую часть участка, при этом в сечении возникает внутренняя продольная сила N3(z.3), где 0<z3</- Определим N3(z3)-ql-qz3=0 N3(z3) =ql + qz3 N3(o)=ql N3(l)=ql +ql = 2ql Определим удлинение стержня: Для этого примем удлинение точки В равным нулю, то есть Хв=0, тогда удлинение точки С можно представить в виде:
=
Удлинение точки D:
Определим диаметр поперечного сечения: Условие прочности при растяжении и сжатии: (Timx (z) < -——— < [<т], где А площадь поперечного сечения А
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ №4 Задача №4 Условие: Стальной стержень с постоянной жесткостью EA=const. нагружен системой сосредоточенныхcwiи распределенной действующей вдоль оси, нагрузкой (рис. 2.6.). Треб уе тся: 1. Определить и построить эпюры продольной силы N(z)линейного перемещения X(z).Из расчета на прочность определить размеры поперечного сечения стержня, принимая его круглым. Определить полную деформацию
Дано: - q = 45 кН, - I = 1.5 м, Е = 210sмПа. - [аст] = 140 мПа. Найти: N(z), Mz), AfJz),d=?
Решение: Для решения данной задачи применим метод сечений, но сначала определим результирующую силу Gраспределенной нагрузки: G= Определим реакцию опоры ZBиз уравнения: 7gl-gl- Разделим тело на два участка – ВС – первый, СD – второй. На каждой из участков проведем сечение перпендикулярное оси z.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

















 =
=  =23,4мм
=23,4мм 
 =
=  =33мм
=33мм

 мм
мм



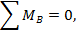

 kH
kH



 =82,1kH
=82,1kH

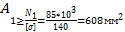 a=24,2мм
a=24,2мм d=14,2мм
d=14,2мм 40X40X4(по ГОСТ8239-72)
40X40X4(по ГОСТ8239-72)


 -
-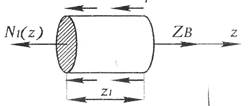 Рассмотрим первый участок ВС:
Рассмотрим первый участок ВС:

 =5gl
=5gl

 +2gl+
+2gl+  =0
=0

 =5gl;
=5gl; =0+
=0+  =
=  =
= 0;
0; 
 =6,1
=6,1  *(-gl
*(-gl 
 ;
;