
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Определение внутренних силовых факторов Q(z) и M(z) и построение их эпюр.Содержание книги
Поиск на нашем сайте
1. Определяем опорные реакции. Для этого мысленно отбрасываем опоры А и В, заменяя их действие опорными реакциями В в неподвижном шарнире А имеем две неизвестные реакции YAи ХА. В неподвижной опоре - одна реакция YB. Определяем их по уравнениям равновесия для всего бруса:
Положительные знаки найденных реакций указывают на то, что принятые направления YА и ХА являются верными. При получении знака «минус» направление опорной реакции должно быть изменено на противоположное. Проверка: 2/3 -ql-2ql+7/3 -ql-ql=0 0=0 2) Определив реакции опор YAи YB, определяем внутренние силовые факторы: Q(z)-поперечная сила M(z)-изгибающий момент. Для определения Q(z) и M(z)применяем метод сечения. Для этого делим балку на участки. Нумерация сделана слева направо (рис.4.5.б.). Балка имеет три участка. На участках проводим сечения. В поперечных сечениях имеет место изгибающий момент M(z)и поперечная сила Q(z). Направления принимаем положительным (рис.4.5.в.). 1. УЧАСТОК 0
Q(y)=YA-qz=2/3ql-qz; Qy=dM(x)/dz; M(z)=2/3 -qlz-qz2/2; Q(z) - изменяется noлинейному закону. M(z) - изменяется noквадратной параболе. Q(0)~2/3 -ql; M(0)=0; Q(2l)=-4/3-ql; M(2l)=-2/3-ql2. На этом участке в точке, где Q(z)=0 изгибающий момент достигает экстремального значения. Q(z)=0; 2/3 -ql-qz-0; z=2/3-l; Mmax(z=2/3 l)=ql2(4/9-4/18)=2/9 l2. 2. УЧАСТОК 2l Q(z)=ql-7/3 -ql=-4/3-ql - const. M(z) =-ql (z)+7/3 ql (z-l)=4/3 qlz-7/3 -ql2- линейный закон. Тогда M(l)= - ql2; M(2l) =1/3 -ql2
Q(z)=F=ql - const. M(z) = -qlz -линейный закон. Тогда М(0)=0; М(l) = -ql2. По этим данным построены эпюры Q(z) и M(z); Масштаб для поперечных сил ql приняты равной 10 мм чертежа. Для изгибающих моментов одна единица принята равной 20 мм на чертеже.
По эпюре изгибающих моментов видно, что наиболее опасным сечением является сечение под опорой В, где / M(z)/=ql2. II. Определение размеров поперечного сечения. Вариант А. И условия прочности балки на изгиб
По таблице сортамента прокатной стали принимаем двутавр N12, у которогоWx=58,4 см2. Вариант Б. Момент сопротивления прямоугольного сечения Wx=
Принимаем b=40мм; h=2,5 b=100 мм. Раздел 5. «РАСЧЕТ РАМ И БРУСЬЕВ СЕЧЕНИЯ ПРИ ИЗГИБЕ И КРУЧЕНИИ» УСЛОВИЯ ЗАДАЧ №9. Задача №9.
На стальную раму действует система внешних сил, как показано на схеме в задании. Номер задания и варианты исходных данных приведены в таблицах №5.1. и №5.2. Требуется:
Определить внутренние силовые факторы (продольные силы, изгибающие моменты и поперечные моменты) и построить эпюры N, Q и М. Из условия прочности определить размеры поперечною сечения рамы, считая ею прямоугольным. 52. СИСТЕМА ЕДИНИЦ И ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ.
ИСХОДНЫЕ ДАННЫЕ К ЗАДАЧАМ.
ПРИМЕР РАСЧЕТА СТАЛЬНОЙ РАМЫ.
Задача №9. Условия: На стальную раму действуют внешние силы (рис. 5.1.). Требуется: Определить и построить эпюры: N(z) — продольной силы; Q(z) — поперечной силы; M(z) — поперечного момента.
Определить размеры поперечного сечения рамы, считая его прямоугольным.
Найти: N(z); Q(y); M(x)
Решение: Заменим опоры реакциями, а распределенную силу результирующей (Рис.5.2.): Для нахождения реакций опор составим уравнения равновесия системы: 1. Уравнение сил относительно оси X:
2. Уравнение моментов относительно точки А: то есть
3) относительно точки E:
Выполним проверку. Для этого составим уравнение моментов относительно точки С:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 920; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.210 (0.008 с.) |

 Х=0; -ХА=0;
Х=0; -ХА=0; -ql2+ YB -3l-ql4=0; YB=7/3-ql.
-ql2+ YB -3l-ql4=0; YB=7/3-ql. (слева)
(слева) (справа)
(справа) 0 (справа)
0 (справа) 
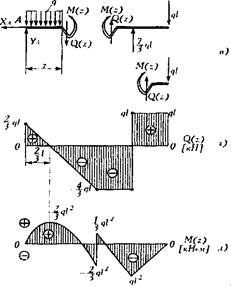 Рис. 4.5.
Рис. 4.5.



 при h=2,5b, Wx=1,04b3;
при h=2,5b, Wx=1,04b3;

















