
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача про завантаження обладнанняСодержание книги
Поиск на нашем сайте
Нехай підприємству задано план виробництва продукції за часом і номенклатурою: треба за час Т виготувати n1, n2, …… nk одиниць продукції Р1, Р2, P3, ……Pk. Продукція обробляється на верстатах S1, S2, S3,……. Sm. Для кожного верстата відома продуктивність аij (тобто кількість одиниць продукції Рj, яку можна виготувати на верстаті Si) і витрати bij на виготовлення продукції Рj на верстаті Si за одиницю часу. Необхідно скласти такий план роботи верстатів (тобто так розподілити обробку продукції між верстатами), щоб витрати на виробництво всієї продукції були мінімальними. Позначимо хij – час, протягом якого верстат Si буде виготовляти продукцію Рj (i=1.2.3…..m, j=1.2.3…..n). Оскільки час роботи кожного верстата обмежений і не перевищує Т, то справедливі нерівності: x1,1+ x1,2 +x1,3 + ……. + x1,k ≤ T x2,1+ x2,2 +x2,3 + ……. + x2,k ≤ T x3,1+ x3,2 +x3,3 + ……. + x3,k ≤ T (4) xm,1+ xm,2 +xm,3 + ……. + xm,k ≤ T Для виконання плану виготовлення за номенклатурою необхідно, щоб виконувались рівності: a11x11+a21x21+……………. + am1xm1 ≤ n1 a12x12+a22x22+ …………… +am2xm2 ≤ n2 …………………………………………. (5) a1kx1k+a2kx2k+………………+amkxmk ≤ nk Крім цього, хij≥0, (i=1.2.3…..m, j=1.2.3…..k) (6) Витрати на виробництво всієї продукції задаються функцією L= b1kx1k+b2kx2k+……+bmkxmk →min (7) Отже, ЕММ задачі про завантаження обладнання має вигляд: Знайти такий розв’язок Х=(x11,x12,x13,…….,xmk), що задовольняє системам (4) – (6), за якою функція набуває мінімального значення. 6. Модель міжгалузевого балансу „Витрати - випуск”. Матричні ЕММ призначені для аналізу та планування виробництва та розподілу продукції на різних рівнях – від окремого підприємства до народного господарства в цілому. Ціль балансового аналізу – відповісти на запитання: яким повинен бути об’єм виробництва кожної з галузей, щоб задовільнити усі потреби в продукції цієї галузі? При цьому кожна галузь виступає, з одного боку, як виробник продукції, а з другого боку як споживач продукції і своєї і інших галузей. Зв’язок між галузями, відображається у таблицях міжгалузевого балансу, а математична модель, яка дозволяє їх аналізувати, розроблена в 1936 році американським вченим В. Леонтьєвим. Основу балансу створює сукупність усіх галузей матеріального виробництва, їх число дорівнює n. Кожна галузь двічі присутня в балансі: як виробник так і як споживач галузі. Як виробнику відповідає визначена строка балансу, а галузі як споживачу визначен стовпець балансу. Якщо номер будь якого виробника галузі позначити через i, аномер будь якої споживчої галузі через j, то величину хij потрібно розуміти як вартість засобів виробництва, вироблених у i -й галузі та спожитої в якості матеріальних витрат в j-й галузі. Матрична модель міжгалузевого балансу
В стовбцях міжгалузевого балансу відображена структура матеріальних витрат та чистої продукції кожної галузі. Припустимо. 1-а галузь – це виробництво електоенергії, друга – вугільна промисловість. Тоді величина х11 показує вартість електроенергії, яку спожила 1-а галузь для своїх внутрішніх виробничих потреб. Величина x12 відображає витрати вугілля при виробництві електроенергії. В цілому ж стовбець х11, x21, х31,..., хn1 характеризує структуру матеріальних витрат за звітний рік в розрезі галузей- постачальників. В балансі відображені не тільки матеріальні витрати, но і чиста продукція галузей. Так, чиста продукція 1-ї галузі характеризується сумою оплати праці v1 та чистого доходу (прибутку) m1. підсумок матеріальних витрат та чистої продукції дорівнює, очевидь, валової продукції галузі (наприклад, для першої галузі – величені Х1). Таким чином, можна записати: Х1=х11+х21+х31+…+хn1+v1+m1 = Такі ж співвідношення вірні і для усіх галузей i мають наступний вигляд: X Якщо подивитися на модель по строкам міжгалузевого балансу, то там представлен розподіл річного об’єму продукції кожної галузі матеріального виробництва. Х1 = х11+х12+х13+ … +х1т+y1 = тоді для будь-якої виробничої галузі Хi= Якщо порівняти ліву та праву частину рівнянь (9) та (10), то можна відмітити, що:
Вираз (11) показує, що в міжгалузевому балансі додержується принцип – єдність матеріального балансу та ватістного складу національного прибутку. Квадрант I – проміжна продукція, показує розподіл матеріальних витрат по усім виробничим галузям. Квадрант II – кінцева продукція, яка вийшла з сфери виробництва та попала в сферу збуту. В розгорнутому вигляді ії можна представити як продукцію, яка іде на власне споживання, на суспільні потреби, а також на поповнення ресурсів та експорт. Квадрант III – характеризує національний дохід з боку його вартісного складу як суму оплати праці та чистого доходу усіх галузей матеріального виробництва. Квадрант IV – відображення кінцевого розподілу та використання національного доходу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.97 (0.006 с.) |

 (8)
(8)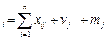 (9)
(9)
 (10)
(10) (11)
(11)


