
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення задач теорії ігор до задач ЛП.Содержание книги
Поиск на нашем сайте
Якщо один з гравців застосовує свою оптимальну стратегію х*, то інший не може покращити своє становище, тобто для оптимальної стратегії справедливі співвідношення:
Перетворимо цю задачу, здійснивши підстановку pi=
Таким чином, маємо задачу ЛП, розв’язуючи яку, отримаємо значення pi, за допомогою яких шляхом оберної підстановки визначимо оптимальні значення ймовірностей, що складають оптимальну мішану стратегію. А здійснивши підстановку qj=
Таким чином, процедура розв’язування гри двох осіб є наступною: 1. Розраховуємо нижню та верхню ціну гри; якщо вони рівні між собою, то гра розв’язана. 2. Спрощуємо гру шляхом виключення домінованих стратегій. 3. Формулюємо пару задач ЛП, розв’язавши одну з яких, встановлюємо оптимальну мішану стратегію одного з гравців (зручніше гравця В). 4. За розв’язком прямої задачі знаходимо розвязок двоїстої. 5. Шляхом оберненої підстановки визначемо оптимальні стратегії для спрощеної гри та доповнюємо їх домінованими чистими стратегіями з ймовірністю використання, що рівні нулю.
Питання для самоконтролю. 1. Дайте визначення гри двох осіб з нульовою сумою. 2. Дайте визначення сідловок точки. 3. Дайте визначення середнього виграшу. 4. Що таке чиста стратегія? 5. що таке мішана стратегія? 6. Що таке домінована стратегія? 7. Сформулюйте основну теорему теорії ігор для двох осіб. 8. Як звести задачу теорії ігор до задачі ЛП?
Тема 8. Аналіз та управління ризиком в економіці Тема 8. Система показників кількісного оцінювання ступеня ризику Лекція 8. Тема лекції: Ризики. Оцінка ризиків. Мета: ознайомити студентів з методами кількісного оцінівання ризиків та методами приняття рішень в умовах невизначеності та ризику.
План лекції 1. Поняття ризику. Причини виникнення, класифікація ризику. 2. Політика управління ризиком. 3. Методи оцінки ризику.
Література: 1. Вітлинський В.В. Аналіз, оцінка і моделювання економічного ризику. - К: ДЕМІУР,1996, – 212 с. 2. Івченко І.Ю. Економічні ризики: Навчальний посібник.- К: «Центр навчальної літератури», 2004. – 304с. 3. Камінський А.Б. Економічний ризик та методи його вимірювання. - К: Козаки, 2002. – 120с. 4. Нейман фон Дж., Моргенштерн О. Теория игр и экономическое поведение. - М: Наука, 1970. – 338с. 5. Трояновский В.М. Математическое моделирование в менеджменте. - М: РДЛ.,2000. – 252с. 6. О.І. Ястремський. Моделювання економічного ризику. - К: Либідь, 1992. – 176с.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

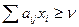 j=
j=  , xi≥0,
, xi≥0,  =1, i=
=1, i= 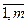 за умов ν→Мах.
за умов ν→Мах. , і отримаємо
, і отримаємо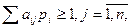
 →Min,тому що ν→Мах.
→Min,тому що ν→Мах. і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:
і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:
 .
.


