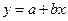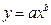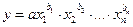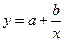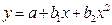Виды производственных функций, их применение в земельном кадастре.

Установленные зависимости могут быть представлены следующими способами: аналитическим (в виде уравнения регрессии), графическим, номографическим, табличным.

В экономической литературе распространение получили следующие виды производственных функций:

1. Линейная:

а) для парной зависимости:

б) для множественной зависимости:

Линейная зависимость применяется в случае равномерного нарастания (убывания) результативного признака с изменением значения фактора производства. Используются в землеустройстве при прогнозировании урожайности сельскохозяйственных культур в зависимости от качества земель, сбора земельных платежей в зависимости от территориальной зоны и т.п.

2. Степенная:

а) для парной зависимости

б) для множественной зависимости

3. Гиперболическая:

Гиперболическая зависимость применяется при изучении обратно пропорциональных связей, когда увеличение факторного показателя в области неотрицательных значений приводит к уменьшению значения результата.

Гиперболические зависимости находят широкое применение при определении различных нормативов, например, при расчете удельных затрат на застройку населенного пункта в расчете на одного жителя в зависимости от площади поселения, и т.д.

4. Полиномная:

Полиномиальная зависимость используется в случае ускоренного возрастания (убывания) результативного показателя при равномерном изменении фактора производства. Например, если получить параболическую зависимость стоимости валовой продукции от размера землепользования, то из нее можно определить такую оптимальную площадь сельскохозяйственного предприятия, при которой будет получена максимальная стоимость валовой продукции (или прибыли).

Во всех функциях при обозначениях принято:

y – результативный показатель,

x1, x2, …,xn – факторы-аргументы,

a, b1, b2, …, bn – параметры уравнений.

Для определения параметров уравнения регрессии (a, b1, b2, …, bn) необходимо решить системы нормальных уравнений. Для парной линейной зависимости.

Использование производственных функций в землеустроительной и кадастровой деятельности рассмотрим на примере решения задачи экономико-статистического анализа состояния использования земельных ресурсов предприятия (муниципального образования и т.д.).

Целью данного анализа является установление факторов, влияющих в наибольшей степени на состояние и использование земельных ресурсов, а также выявление эффективных направлений реорганизации территории и производства.

В качестве результативного показателя, характеризующего уровень интенсивности использования земель, рекомендуется брать общую величину поступления земельного налога в бюджет административно-территориального образования в стоимостном выражении (у). В этом показателе аккумулируются результаты развития рынка земель в соответствующем регионе.

Отбор факторов-аргументов производится в две стадии. На первой – путем логического анализа отбираются факторы-аргументы, оказывающие влияние на уровень использования земель, на второй – методом корреляционного анализа выделяются те из них, которые имеют особенно тесную связь с использованием земель. При этом факторы-аргументы, которые взаимодействуют друг с другом или находятся между собой в функциональной зависимости, в модель не включаются. Это взаимодействие (коллинеарность) выявляется по величине парных и частных коэффициентов корреляции.

Отбор признаков для включения их в корреляционную модель должен базироваться на знании теоретических основ и практическом опыте. Для этого используются статистические ряды, графики, применяются статистические группировки по факторным или результативным признакам. Практика показала, что при выборе формы связи между результативным показателем, характеризующим использование земель, и факторами-аргументами, чаще всего применяются линейные уравнения множественной регрессии и многофакторные степенные функции.